Диафрагмы не рекомендуется приваривать к поясу в зоне подошвы рельса, обеспечивая их плотное прилегание к рельсу.
К стенкам балок целесообразно приваривать диафрагмы двухсторонним швом с полным проваром.
Продольные ребра жесткости, обеспечивающие местную устойчивость стенок балки, сами должны обладать необходимой жесткостью и прочностью.
В качестве продольных ребер жесткости могут использоваться листы, уголки, швеллеры или гофры.
Продольные ребра жесткости для стенок ставятся на расстоянии от крайней сжатой кромки стенки:
- при одном ребре b 1=(0,2…0,25) h;
- при двух ребрах b 1=(0,15…0,2) h; b 2=(0,32…0,4) h.
Требуемые значения момента инерции продольного ребра относительно плоскости стенки определяют по рекомендациям ВНИИПТМАШ [4] в соответствии с табл. 8.2.
| Таблица 8.2 Расчетные моменты инерции продольного ребра | |||
| b 1/ h | Необходимый момент инерции продольного ребра | Предельные значения | |
| минимальные | максимальные | ||
| 0,2 | 
| 
| 
|
| 0,25 | 
|
| 
|
| 0,3 |
| ||
Варианты установки продольных ребер показаны на рис. 8.3.
Продольные ребра размещают между большими диафрагмами, не сваривая между собой диафрагму и продольное ребро. Вместо привариваемых ребер может быть использован листовой прокат с гофрами (рис. 8.4).
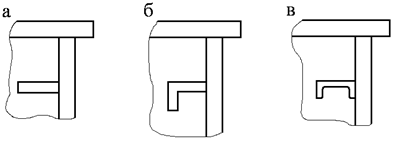Рис. 8.3. Варианты ребер жесткости из проката
|
| ||
| ||
| B | B 1 | B 2 |
| Рис. 8.4. Листовой прокат с закрытыми периодически повторяющимися гофрами (ТУ-14-2-280-77) |
9. Сварные соединения
элементов металлических конструкций
9.1. Общие положения
Для соединения элементов металлоконструкций грузоподъемных кранов при толщине свариваемых элементов до 50 мм используется преимущественно автоматическая, полуавтоматическая и ручная дуговая сварка металлическими электродами. Данные по характеристикам сварочных материалов приведены в табл. 1.5.
|
|
Основные типы и конструктивные элементы соединений должны соответствовать действующим стандартам. Наиболее применяемыми являются:
| ГОСТ 5264—80*. | Ручная дуговая сварка. Соединения сварные. Основные типы, конструктивные элементы и размеры. |
| ГОСТ 11534—75*. | Ручная дуговая сварка. Соединения сварные под острыми и тупыми углами. Основные типы, конструктивные элементы и размеры. |
| ГОСТ 14771—76*. | Дуговая сварка в защитном газе. Соединения сварные. Основные типы, конструктивные элементы и размеры. |
| ГОСТ 23518—79*. | Дуговая сварка в защитных газах. Соединения сварные под острыми и тупыми углами. Основные типы, конструктивные элементы и размеры. |
В условиях завода-изготовителя применяются автоматическая и полуавтоматическая сварка с физическими методами контроля швов, что обеспечивает высокое качество.
При монтаже и ремонте конструкций используется обычно ручная сварка. Возможности применения физических методов контроля зачастую весьма ограничены.
В соответствии с требованиями ПБ10-382-00 [3] все сварные соединения подлежат 100% визуальному контролю. Контроль сварных соединений просвечиванием производится в начале и конце швов стыковых соединений поясов и стенок коробчатых балок, при этом суммарная длина контролируемых участков должна составлять не менее 50% от длины стыка растянутого пояса, 25% всех остальных стыковых соединений и 25% от длины шва других видов сварных соединений, указанных в рабочих документах.
|
|
Сварные соединения выполняются стыковыми и угловыми швами. Соединения с угловыми швами различают по типу взаимного расположения элементов: тавровые, нахлесточные и угловые.
9.2. Стыковые соединения
Стыковые соединения используются главным образом для изготовления длинномерных элементов: полотнищ из листового или широкополосного проката для листовых конструкций (балок), а также элементов из фасонного проката для ферменных конструкций в тех случаях, когда размеры элементов превышают товарную длину проката.
При изготовлении коробчатых балок должны выполняться следующие требования [17, 18]:
- между стыками полотнища расстояние должно быть не менее 4000 мм;
- длина пристыкованного элемента должна быть не менее 500 мм, если это не оговорено чертежом, и стык должен располагаться у конца основного элемента;
- стыки стенок должны располагаться на расстоянии не ближе 2000 мм от середины пролета балки;
- стыки поясов должны быть смещены относительно друг друга и располагаться на расстоянии не мене 150 мм от стыков стенки;
- стыки поясов и стенок должны располагаться на расстоянии не менее 50 мм от диафрагм.
При правильном выборе сварочного материала, при контроле шва физическими методами и выведении концов шва на выводные планки соединения принимаются равнопрочными основному металлу и не требуют дополнительного расчета на статическую прочность.
9.3. Соединения с угловыми швами
9.3.1. Расчетные сечения соединений
В соответствии с рекомендациями сварные соединения с угловыми швами при действии продольной и поперечной сил следует рассчитывать на срез (условный) по двум сечениям: по металлу шва (сечение Ш, рис. 9.1) и по границе сплавления (сечение Г).
|
|
| Рис. 9.1. Сечения углового шва |
Расчетные напряжения:
- по металлу шва (сечение Ш)
, (9.1)
- по границе сплавления (сечение Г)
, 
(9.2)
; 
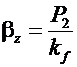, (9.3)
где lw — расчетная длина шва; kf — размер катета шва; β z, β f — коэффициенты, учитывающие геометрию шва; Rwz, Rwf — расчетные сопротивления металла шва (см. табл. 1.5).
Для расчета соединения на срез достаточно рассматривать менее прочное сечение, рекомендации по назначению которого приведены в табл. 9.1, в зависимости от временного сопротивления стали сопрягаемых элементов растяжению R ИП, нормативного сопротивления металла шва RW ИП и коэффициента β f, характеризующего вид сварки, положение шва и толщину свариваемых элементов.
| Таблица 9.1 Расчетные сечения соединений с угловыми швами | ||||
| Временное сопротивление стали сопрягаемых элементов растяжению R ИП, МПа | β f | Нормативное сопротивление металла шва по временному сопротивлению RW ИП, МПа | ||
| 345-380 | 1,1 0,9 0,7 | г ш ш | г г ш | г г ш |
| 390-410 | 1,1 0,9 0,7 | ш ш ш | г ш ш | г г ш |
| 430-460 | 1,1 0,9 0,7 | ш ш ш | ш ш ш | г ш ш |
| 470-490 | 1,1 0,9 0,7 | ш ш ш | ш ш ш | ш ш ш |
При автоматической и полуавтоматической сварке и при катетах швов, равных толщине свариваемых элементов, рекомендуется:
| при | kf  12 мм
| β f =1,1, | β Z =1,15; |
| kf = 14…16 мм | β f =0,9, | β Z =1,05; | |
kf  18 мм
| β f =0,7, | β Z =1,0. |
При ручной сварке β f =0,7, β Z =1,0.
Для фланговых швов, расположенных вдоль направления действия усилия, в связи с неравномерностью распределения касательных напряжений среза по длине значение расчетной длины ограничивается условием:
lw ≤85β f kf. (9.4)
Для швов, в которых усилие приложено по всей длине шва (например, поясные швы балок) расчетная длина не ограничивается.
9.3.2. Тавровые соединения
Поясные швы балок.
Проверка прочности швов, соединяющих пояса и стенки балок при отсутствии местной сосредоточенной нагрузки, выполняется по формуле
,(9.5)
где Q — поперечная сила в рассчитываемом сечении;
S БР — статический момент полусечения балки брутто;
J БР — момент инерции сечения балки брутто.
При местной сосредоточенной нагрузке, в частности при расположении подтележного рельса над стенкой, давление колеса вызывает появление дополнительных касательных напряжений [19]:
, (9.6)
где P — сосредоточенная нагрузка (например, давление колеса тележки); n — коэффициент, зависящий от характера обработки кромок, при полном проваре можно принимать n =0,4; z — расчетная длина шва, по которому происходит передача давления с пояса на стенку,
, (9.7)
где J Р, J П — собственные моменты инерции рельса и пояса; dП — толщина пояса.
Прочность шва при наличии местного давления определяется по условию:
. (9.8)
Нагрузки в плоскости, перпендикулярной расположению швов.
Схема нагружения соединения показана на рис. 9.2.
Проверка прочности швов при действии момента М производится по условию:
, (9.9)
. (9.10)
| Рис. 9.2. Схема нагружения таврового соединения |
При действии отрывающей нагрузки N расчет швов выполняется по формуле
. (9.11)
В зависимости от степени глубины провара при выполнении соединения рассматриваются схемы, показанные на рис. 9.3.
При полном проваре с разделкой кромок (рис. 9.3, а, б) швы принимаются равнопрочными с основным металлом.
При неполном проваре (рис. 9.3, в, г) швы проверяют с учетом условной толщины t У:
- по металлу шва
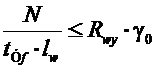; (9.12)
Рис. 9.3. Схема к расчету тавровых соединений:
а — с двухсторонней разделкой кромок с полным проваром; б — с односторонней разделкой кромок с полным проваром; в — с двухсторонней разделкой кромок с неполным проваром; г — без разделки кромок с неполным проваром
|
- по границе сплавления
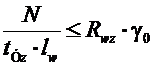, (9.13)
где h К — глубина разделки кромок (см. рис. 9.3, в) или проварка (см. рис. 9.3, г);
t У f =2,6 h К, t У z =2,8 h К. (9.14)
Дополнительно проверяются соединения по основному металлу в сечении А — А, перпендикулярном к направлению силы N:
, (9.15)
где Rth — расчетное сопротивление растяжению основного металла в направлении толщины проката (см. табл. 1.2).
Условная толщина:
| t У=1,3 t С — для схемы рис. 9.3, а; |
| t У=1,15 t С — для схемы рис. 9.3, б; |
| t У=2(h К+0,25 t С) — для схемы рис. 9.3, в; |
| t У=2,8β f kt — для схемы рис. 9.3, г. |
При действии изгибающего момента в плоскости, перпендикулярной сечению А — А, проверка производится по формуле (9.9) при
. (9.16)
9.3.3. Нахлесточные соединения
Нахлесточные соединения применяются главным образом как соединения монтажные. При монтаже стыков коробчатых балок используются односторонние накладки.
Схемы к расчету нахлесточных соединений [19] при действии продольного усилия, расположенного в плоскости соединения, показаны на рис. 9.4, а, б.
Как видно из рис. 9.4, напряжения как в швах, так и в металле соединяемых элементов распределяются весьма неравномерно.
Рис. 9.4. Распределение напряжений в нахлесточном соединении:
а – сварка только фланговыми швами; б – фланговыми и лобовым швами
|
По упрощенной методике, приведенной в [4], неравномерность распределения напряжений в швах компенсируется снижением расчетных сопротивлений материала швов (см. табл. 1.5), и проверка прочности швов производится по формулам (9.1) или (9.2), в которых величина lw принимается равной сумме длин как фланговых, так и лобовых швов.
Результаты исследований, приведенные в [19], позволяют более точно определить величины действующих напряжений. При использовании только фланговых швов (см. рис. 9.4, а) касательные напряжения в швах
; (9.17)
; (9.18)
. (9.19)
Коэффициент концентрации k t при отношениях 
равных 10, 20, 30 и 40 составляет 2,19, 3,1, 3,79 и 4,38 соответственно.
В связи с резким возрастанием неравномерности распределения касательных напряжений при увеличении длины шва максимальную его длину целесообразно ограничить величиной lw [40b f kf, а минимальную длину принимать lw /6b f kf /40 мм.
Усилия в соединяемых элементах передаются через сварные швы. Характер распределения напряжений по ширине элементов также показан на рис. 9.4, а.
, (9.20)
. (9.21)
Значения k s в зависимости от соотношения a / l:
a/l 0,1 0,5 1,0 2,0
k s 1,45 2,01 3,37 6,61
При использовании одновременно фланговых и лобовых швов (рис. 9.4, б) неравномерность распределения касательных и нормальных напряжений существенно снижается, ввиду чего можно использовать упрощенную методику [4].
В обоих вариантах в сечении А — А из-за эксцентриситета сечения возникает (см. рис. 9.4, б) местный изгибающий момент
, (9.22)
, (9.23)
и, следовательно, возникают местные нормальные напряжения
. (9.24)
Прочность соединительной накладки должна проверяться по условию:
. (9.25)
Расчетная схема соединения при действии момента в плоскости соединения показана на рис 9.5.
| Рис. 9.5. Расчетная схема при действии момента в плоскости соединения |
Проверка прочности металла шва производится по условию [4]:
, (9.26)
где 
— наибольшее расстояние от центра тяжести шва (т. О) до крайней точки шва; JP — полярный момент инерции соединения относительно центра тяжести,
JP = Jx + Jy, (9.27)
где Jx, Jy — осевые моменты инерции плоскостей среза швов относительно центральных осей Ox и Oy.
10. Пример расчетов
металлических конструкций
10.1. Исходные данные
Для примера расчета возьмем мост крана грузоподъемностью 32 т с коробчатыми сплошностенчатыми балками, с рельсом, расположенным по оси верхнего пояса (рис. 10.1).
Рис. 10.1. Металлоконструкция кранового моста
|
Кран эксплуатируется при температуре выше минус 20°С, пролет крана — 22,5 м, скорость передвижения крана — 1,20 м/с, высота подъема груза — 28 м, скорость подъема — 0,17 м/с, группа классификации (режима) работы крана — А4.
В дополнение к этим исходным данным берем из курсового проекта по дисциплине «Грузоподъемные машины» значение веса тележки, ее колеи и базы, если, конечно, совпадают грузоподъемности, или эти параметры задаются преподавателем. В нашем случае принимаем колею тележки В Т=3,4 м, базу L Т=3,2 м. Вес тележки определим по соотношению G Т=(0,25…0,35) G Г, т. е.
G Т = 0,287·32·9,81 = 90 кН.
10.2. Выбор материала конструкции
Учитывая, что проектируемый кран будет эксплуатироваться при температуре выше минус 20°С, в качестве материала для основных несущих элементов в соответствии с данными табл. 1.1 принимаем малоуглеродистую сталь Ст.3сп5 по ГОСТ 380—94.
Расчетное сопротивление материала при растяжении, сжатии и изгибе Ry=Ry П / γ m (см. табл. 1.2), где Ry П=255 МПа – нормальное сопротивление, принимаемое равным пределу текучести; γm=1,05 – коэффициент надежности по материалу.
Таким образом, Ry = 255/1,05 = 243 МПа.
Расчетное сопротивление при сдвиге (срезе)
RS = 0,58× Ry П / γm = 0,58 × 255/1,05 = 141 МПа.
Расчетные сопротивления стыковых сварных швов при растяжении, сжатии, изгибе Rwy=Ry =243 МПа (см. табл. 1.3). Расчетные сопротивления стыковых сварных швов при сдвиге Rws=Rs =141 МПа (см. табл. 1.5).
Расчетные сопротивления металла углового шва при срезе Rwf =(0,55 Rwу П )/ γ =0,55×410/1,25 = 180 МПа (см. табл. 1.5 и 1.7), где Rwу П = 410 МПа — нормативное сопротивление материала шва (см. табл. 1.6); γ=1,25 — коэффициент надежности.
10.3. Расчетные нагрузки
При определении прочности металлоконструкций расчетные нагрузки рассматриваются при комбинации II А, при этом тележка находится в середине пролета моста и производится подъем груза.
10.3.1. Нагрузки от веса моста
Для заданных параметров пролета крана при выбранной общей схеме его исполнения и принятом материале по графикам рис. 4.1 находится в качестве первого приближения нормативный вес моста G МК=270 кН. Расчетный вес полумоста (см. табл. 3.1)
,
а расчетный погонный вес полумоста (без веса кабины и приводов механизма передвижения)
.
10.3.2. Нагрузки от веса кабины
и механизмов передвижения
Нормативный вес кабины (закрытой, с электрооборудованием) принимаем G КН=14 кН. Расчетный вес кабины G К =G КН ×γ К=14×1,2 = 16,8 кН. Кабина располагается таким образом, чтобы между задней стенкой и осью подкранового рельса было не менее 1000 мм. Принимаем расстояние от середины кабины до подкранового рельса а 2=2,5 м.
Нормативный вес привода механизма передвижения моста крана в первом приближении [2] можно определить, воспользовавшись табл. 7.2, в которой приведены данные по раздельному механизму передвижений кранов (типоразмеры двигателей, тормозов, ходовых колес) грузоподъемностью (5…320) т.
По данным этой таблицы нормативный вес каждого привода крана грузоподъемностью 32 т составляет примерно 6 кН. Тогда расчетный вес одного привода
,
где γ — коэффициент надежности по нагрузке (см. 4.1.2).
10.3.3. Нагрузки от веса груза и тележки
Нормативный вес груза рассматриваемого крана
G=Q Н g = 32×9,81=314 кН.
Расчетный вес груза 
,
где 
=1,15 — коэффициент динамичности по графику (см. рис.4.2); γ Q= 1,12 — коэффициент надежности по нагрузке для веса груза (см. табл. 4.2).
Ориентировочно нормативный вес тележки принимается по ИСО 4301/1-А4 в зависимости от режимной группы А4 (см. стр. 23) – G ТН = 90 кН.
Расчетный вес тележки
G Т= G ТН×γ=90×1,2=108 кН,
где γ=1,2 — коэффициент надежности по нагрузке.
Расчетные усилия на ходовые колеса от веса груза и тележки для рассматриваемого крана с достаточной точностью можно принять одинаковыми:
.
10.4. Наибольший изгибающий момент
от вертикальных нагрузок
Наибольший изгибающий момент от подвижной нагрузки возникает в сечении, смещенном от середины пролета на расстояние В Т/4(В Т – база тележки), при расположении тележки соответствующим колесом над указанным сечением, т. е. это сечение отстоит от опоры В на расстоянии (рис. 10.2)
Z 0= 0,5(L — b 1) = 0,5×(22,5—1,6)=10,45 м,
где b 1 — половина базы тележки.
Наибольший момент от подвижной нагрузки
.
Здесь DR =2 D — равнодействующая усилий колес на пролетную балку.
Рис. 10.2. Вертикальные нагрузки и эпюры изгибающих моментов пролетной балки
|
В этом же сечении балки изгибающие моменты от распределенной нагрузки q ПМ
и от неподвижных сосредоточенных нагрузок G ПР и G К (вес приводов и кабины)
.
Здесь а1 =1,2 м и а 2=2,5 м по рис. 10.1.
Суммарный расчетный изгибающий момент
.
10.5. Определение оптимальных размеров поперечного сечения пролетной балки
10.5.1. Расчет размеров в средней части пролета
из условия обеспечения прочности
Схема расчетного поперечного сечения двояко-симметричной балки с рельсом по оси пояса приведена на рис. 10.3.
Рис. 10.3. Поперечное сечение балки
|
Расчет проводим по первому предельному состоянию (потеря несущей способности) при действии нагрузок комбинации II А (см. табл.3.1).
Необходимая величина момента сопротивления балки при изгибе в вертикальной плоскости
,
где γ0=γ1γ2γ3 — коэффициент неполноты расчета. γ1=0,90; γ2=0,95; γ3=0,90 (см. табл. 5.1, 5.2 и 5.3).
Подставляя в формулу численные значения параметров и коэффициентов, имеем
.
Оптимальная по условию минимума веса толщина стенки балки (если принять H» h) при обеспечении ее прочности
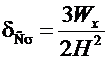, (10.1)
где H — высота стенки.
Это равенство не позволяет однозначно определить толщину стенки, так как в нем неизвестны H и δС. Реальная высота балки у существующих мостовых кранов колеблется в пределах 1,0…1,8 м. Определим толщину стенки при различной ее высоте по формуле (10.1) для Н С1=1,0 м, Н С2=1,2 м, Н С3=1,4 м, Н С4=1,6м, Н С5=1,8 м. Результаты расчета введем в табл. 10.1.
10.5.2. Расчет размеров в средней части пролета
из условия обеспечения статической жесткости
Минимальный момент инерции балки при обеспечении нормальной величины статического прогиба моста (см. табл. 5.6 и формулу (5.8)) при нормативных подвижных нагрузках