Взаимное положение графиков Нs и Н f зависит от конкретных параметров крана, например, как показано на рис. 5.2. При ином соотношении параметров крана эти графики могут и не пересекаться. Определяющим фактором должна приниматься бóльшая из расчетных значений высота. Так, на рис. 5.2 на участке АВ размеры балки должны назначаться из условия её жесткости, а на участке ВС — из условия прочности.
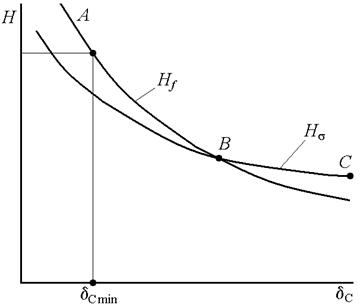
| Рис. 5.2. Выбор толщины стенки при S=300 |
По рекомендации ВНИИПТМАШ гибкость стенки (отношение высоты стенки к её толщине) рационально принимать не больше 300.
Дополнительным критерием выбора высоты балки может быть сравнение с выполненными конструкциями. Обычно у кранов грузоподъемностью 5…50 т высота балки составляет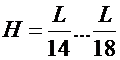 
, а у кранов грузоподъемностью 80…320 т 
.
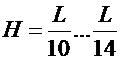С увеличением толщины проката его прочностные характеристики снижаются, в связи с чем рекомендуется применять листовой прокат из углеродистой стали толщиной до 50 мм, а из низколегированной стали – толщиной до 40 мм.
Ширина пояса для обеспечения жесткости балки в горизонтальной плоскости принимается
,
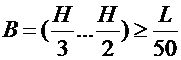где L — пролет крана.
Считается, что оптимальная толщина пояса получается, когда площадь пояса равна одной трети площади стенки.
Тогда
, (5.10)
при этом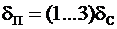 
.
Иногда при определении толщины пояса используют следующие выражения:
, (5.11)
или
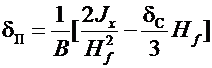. (5.12)
Так как Wx и Jx определены из различных условий, формулы (5.11) и (5.12) не эквивалентны.
Для обеспечения устойчивости верхнего пояса размер b между стенками балки из стали Ст. 3 при расчетном сопротивлении R= 225 МПа должен быть не более чем
b≤ 60 δП, (5.13)
при других расчетных сопротивлениях R эту величину необходимо умножать на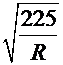 
.
Из условия возможности приварки диафрагмы к стенке и поясу этот же размер в зависимости от высоты балки должен корректироваться в пределах не менее 300…500 мм.
|
|
При необходимости отступления от оптимальной высоты для сохранения толщины стенки δ С и заданного момента сопротивления Wx толщину пояса можно принимать
, (5.14)
а при сохранении заданного момента инерции Jx
, (5.15)
где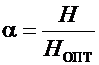 
; Н — принятая конструктивная высота балки.
После этого окончательно назначаются размеры поперечного сечения главной балки в средней части пролета и определяются её фактические геометрические характеристики. Проверка прочности балок на действие нагрузок II Б и II В производится после подбора размеров концевых балок и компоновки узлов сопряжения пролетных и концевых балок.
6. Расчет размеров поперечного сечения
пролетной балки с рельсом над стенкой
6.1. Общие положения
Пролетные балки с рельсом над стенкой имеют более высокую степень использования материала, чем симметричные балки с рельсом на поясе. Это связано, в первую очередь, с тем, что верхний пояс может использоваться в качестве площадки для обслуживания тележки и, следовательно, не требуется устраивать специальные площадки, как это делается на кранах с балками обычной конструкции. При достаточных размерах внутри балки могут размещаться приводы механизмов передвижения крана и электрооборудование.
Типовое поперечное сечение балки показано на рис. 6.1.
Высота балки рассчитывается так же, как и высота балки с рельсом на поясе. Ширина балки В =(0,8…1,0) Н. Толщина стенок δ1>δ2, толщина поясов δ3≥δ1. Поперечные ребра жесткости выполняются в виде рам и располагаются с шагом а =(1/10…1/14) L в зависимости от конструкции и устойчивости стенок и верхнего пояса. Верхний пояс подкрепляется одним или двумя продольными ребрами жесткости. Необходимость применения продольных ребер на стенках определяется устойчивостью последних.
|
|
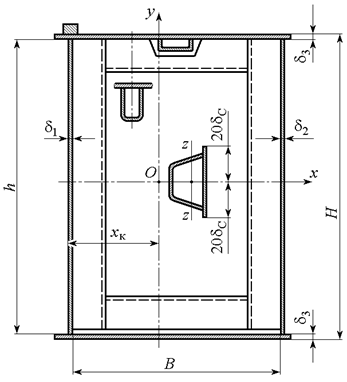Рис. 6.1. Схема поперечного сечения балки с ребрами жесткости
|
Вертикальное давление колес тележки, приложенное эксцентрично по отношению к центру кручения (т. О), вызывает скручивание балки.
Коробчатые балки имеют высокую крутильную жесткость, поэтому касательные напряжения от кручения настолько малы, что ими пренебрегают. Однако эксцентричное приложение нагрузки вызывает появление дополнительных поперечных сил как в стенках, так и в поясах, и касательные напряжения от этих сил могут быть достаточно велики. Кроме того, эксцентричная нагрузка вызывает деформацию поперечных рамных диафрагм, что также должно быть учтено при расчетах.
6.2. Расчет размеров поперечного сечения
Условия обеспечения общей прочности и жесткости балки не зависят от типа её поперечного сечения. В связи с этим величину момента сопротивления Wx определяют по формуле (5.1) с учетом коэффициента неполноты расчета (см. табл. 5.1…5.5) по формуле (5.2). Величина момента инерции Jx определяется по формулам (5.8) или (5.9).
Поскольку стенки балки будут иметь различную толщину (δ1>δ2), приняв
δС=δ1+δ2, (6.1)
оптимальные высоты по условиям прочности и жесткости можно определить по выражениям
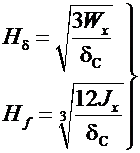. (6.2)
Для наглядности целесообразно построить графики H δ и Нf по аналогии с графиками рис. 5.2 и для дальнейших расчетов принять бóльшее из их значений.
|
|
При одинаковой высоте балки гибкость стенок будет различной и использовать ее в качестве критерия неудобно. Рациональнее воспользоваться аналогией с выполненными конструкциями. Обычно у кранов общего назначения грузоподъемностью 5…50 т высота балок Н =(1/14…1/18) L, [1, 2], а у кранов грузоподъемностью 80…320 т Н =(1/10…1/14) L, где L – пролет крана. Тогда в этих диапазонах суммарная толщина стенок может быть определена из функции
δС=(δ1+δ2)=3 W x/Hs, (6.3)
или
δС=(δ1+δ2)=6 Wx/Hf 2. (6.4)
Следует иметь в виду, что величины Wx и Jx определены исходя из различных условий, поэтому величины δС по формулам (6.3) и (6.4) в общем случае различны.
По технологическим причинам минимальная толщина стенки принимается не менее 5 мм. С точки зрения обеспечения местной устойчивости гибкость свободной стенки целесообразно ограничить: для углеродистых сталей S ≤ 265, для низколегированных сталей S ≤ 225…240, что дает возможность обойтись установкой одного продольного ребра жесткости.
Ширина пояса принимается В =(0,8…1,0) Н.
Тогда для оптимальной балки при выбранном значении высоты Н и сохранении значений Wx или Jx толщина пояса может быть определена по выражениям
(6.5)
или
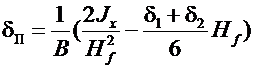. (6.6)
С учетом замечаний к формулам (5.3) и (5.4) следует, что формулы (6.5) и (6.6) не эквивалентны друг другу.
Желательно, чтобы δП ≥ δ1, а если при этом расстояние между стенками в > 60δП, то пояс необходимо укреплять продольным ребром жесткости.
Продольные ребра стенок и пояса приварены по всей длине к поясу, стенкам и поперечным ребрам жесткости. В связи с этим они должны быть включены в расчетное сечение балки и, следовательно, фактические геометрические характеристики поперечного сечения должны определяться после окончательного выбора всех размеров, в том числе и продольных ребер жесткости.
6.3. Нагрузки от эксцентриситета
При приложении нагрузки к одной из стенок возникает скручивающий балку момент, что приводит к перераспределению нагрузок на элементы поперечного сечения балки.
Схема нагрузок в этом случае [13] показана на рис. 6.2.
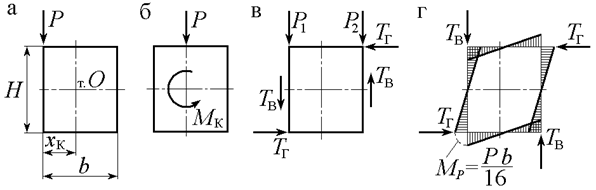Рис. 6.2. Схемы к расчету балки и диафрагмы-рамы:
а, б — внешние усилия; в — усилия по контуру рамки; г — эпюра изгибающих моментов от крутящего момента
|
Координата центра кручения (т. О) в зависимости от соотношения размеров определяется по графикам рис. 6.3, на котором h=d2/d1; m2=d3/d1. Отношение m1= H / b на графиках принято равным единице.
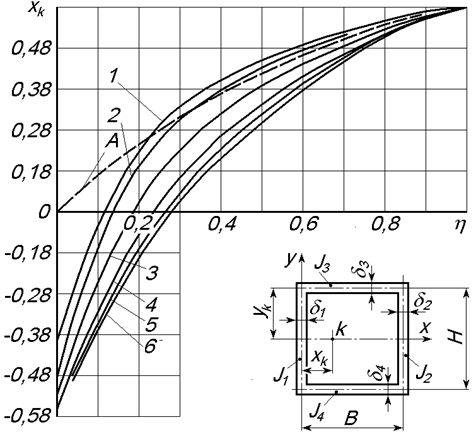Рис. 6.3. Графики зависимости x К от μ2=δ3/δ1:
1 — μ2=0,25; 2 — 0,50; 3 — 1,0; 4 ‑‑ 2,0; 5 ‑‑ 3,0; 6 — 5,0; А — x К= 
|
Крутящий момент
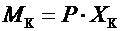. (6.7)
Нагрузки по элементам балки (рис. 6.2, в, г):
, 
, 
, 
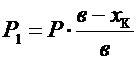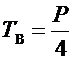. (6.8)
Изгибающие моменты в углах рамки
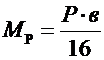. (6.9)
Исследования [13] показывают, что наличие эксцентриситета не влияет на величину изгибающего момента и соответствующих ему нормальных напряжений. Нормальные напряжения от стесненного изгиба и касательные напряжения от кручения балки малы и ими можно пренебречь. Таким образом, эксцентриситет нагрузки вызывает появление дополнительных нагрузок Т В на стенки и Т Г на пояса и, следовательно, появление дополнительных касательных напряжений от действия поперечных сил, которые нужно учесть при расчетах, а также деформацию рамки-диафрагмы.
6.4. Прочность и устойчивость стенок
6.4.1. Стенка под рельсом
Стенка под рельсом нагружена нормальными напряжениями от общего изгиба, местными нормальными напряжениями от давления колес тележки и касательными напряжениями среза от поперечной силы при общем нагружении балки и дополнительными касательными напряжениями от эксцентриситета нагрузки.
Нормальные напряжения в стенке от общего изгиба на уровне верхнего пояса
, (6.10)
где М — общий изгибающий момент для балки по формуле (4.2); h — высота стенки; Jx — общий момент инерции балки.
Местные напряжения сжатия на кромке стенки от давления колеса, передающегося на стенку через рельс и пояс,
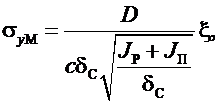(6.11)
где s y М — местные напряжения сжатия кромки стенки в вертикальной плоскости; D — давление колеса; с — коэффициент, учитывающий способ соединения пояса и стенки; для сварных и прокатных балок с =3,25, для клепаных с =3,75; δС — толщина стенки; J Р и J П — моменты инерции рельса и пояса относительно собственных нейтральных осей; ξ — коэффициент, учитывающий разгружающее влияние поперечных ребер жесткости.
При определении J П в расчет вводится часть пояса шириной от его наружного края до расстояния 10…12 значений толщины пояса от оси стенки внутрь балки, но не менее ширины подошвы рельса.
График коэффициентаξ для сварных балок приведен на рис.6.4. На графике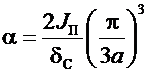 
, (6.12)
где а – расстояние между ребрами жесткости.
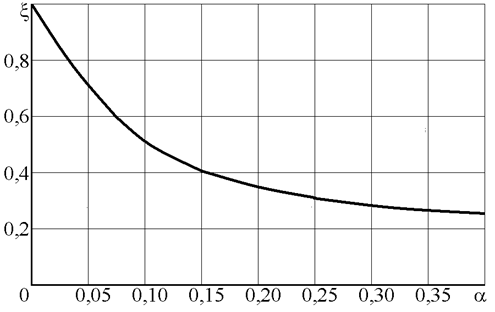Рис. 6.4. График коэффициента влияния ребер ξ
|
Влияние ребер практически не сказывается (ξ=1) при а =70 δ, а заметное уменьшение местных напряжений на кромке стенки получается лишь при а =(40…50)δС. Так часто целесообразно располагать лишь короткие ребра, длина которых должна быть не менее 0,3 h, где h — высота стенки.
Касательные напряжения среза от суммарной поперечной силы (см. формулу 6.8)
(6.13)
в предположении, что её воспринимает только стенка,
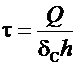. (6.14)
Прочность стенки при плоском напряженном состоянии проверяется по условию:
, (6.15)
где γ0 — коэффициент неполноты расчета (по формуле (5.2) и табл. 5.1…5.5); Ry – расчетное сопротивление материала (табл. 1.2, 1.3).
Устойчивость стенки при действии только касательныхнапряжений проверяется по указаниям раздела 8.3.4.
При совместном действии нормальных напряжений от общего изгиба балки σz и местных нормальных напряжений, а также касательных напряжений τ местная устойчивость проверяется по условию:
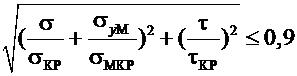. (6.16)
Величина критических напряжений среза τ КР определяется по формуле (8.9). Критические нормальные напряжения существенно зависят от соотношения размеров отсека пластинки а/h, где а — шаг диафрагм, и от соотношения местных и общих нормальных напряжений в соответствии с данными табл. 6.1.
| Таблица 6.1 Коэффициенты для проверки устойчивости стенок сварных коробчатых балок [1] | ||||||||
| Коэффи-циенты | а/h | |||||||
| 0,5 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | |
| К 1 | ||||||||
| σМ/σ | 0,112 | 0,300 | 0,633 | 1,283 | 2,249 | 3,939 | ||
| К 2 | ||||||||
| Примечание. При а/h > 2 значения коэффициентов равны их величинам при а/h =2,0 |
При а/h ≤0,8 критические напряжения от общего прогиба
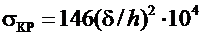, МПа, (6.17)
а от местного напряжения
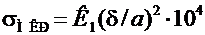, МПа.(6.18)
При а/h =0,8, если σМ/σбольше значений, указанных в табл.6.1, то местные критические напряжения
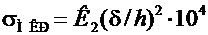, МПа;(6.19)
если σМ/σне больше значений, указанных в табл.6.1, то местные напряжения определяются по формуле (6.18), но с подстановкой а /2 вместо а как в формулу (6.18), так и в табл. 6.1.
В обоих случаях τ КР вычисляется по действительным размерам отсека.
При высоких значениях сжимающих напряжений для устойчивости стенки применяют кроме основных поперечных ребер жесткости продольные ребра на расстоянии (0,25…0,3) h от сжатого пояса и доходящие до продольного ребра короткие поперечные ребра. В этом случае каждый отсек проверяется отдельно (см. 8.3.5) с учетом приведенных выше формул для определения критических напряжений.
6.4.2. Свободная стенка
Прочность и устойчивость свободной стенки проверяется по методике, приведенной в 8.3.4 и 8.3.5.
6.5. Расчет
основной поперечной диафрагмы – рамы
Основные диафрагмы обеспечивают устойчивость стенки и поперечную жесткость сечения балки.
Для обеспечения местной устойчивости стенки величина момента инерции ребра должна быть не менее
J1≥ 3 h δС; (6.20)
при вычислении J 1 учитывается часть стенки шириной 20 δС в обе стороны от оси ребра (см. рис. 6.1).
Для ограничения деформации рамы требуемый момент инерции ребра относительно оси Z
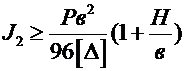, (6.30)
где [∆] — допускаемая деформация рамы (противоположный вертикальный сдвиг обеих стенок); [∆]=(0,001…0,002) в.
Нормальные напряжения в углах рамы (см. рис. 6.2, г)
, (6.31)
где Wz — момент сопротивления ветви рамы относительно оси Z (см. рис. 6.1).
Таким образом, определение размеров ребра рамы будет производиться методом подбора.
6.6. Продольные ребра жесткости
Расчет необходимых параметров продольных ребер жесткости производится по методике, приведенной в п. 8.3.6.
После окончательного назначения всех размеров сечения и ребер жесткости расчитываются геометрические характеристики поперечного сечения для средней части пролета главной балки.
7. Компоновочные схемы мостов
7.1. Общие принципы компоновки
Компоновка мостов кранов общего назначения определяется как конструктивным решением пролетных частей, так и, в бόльшей степени, компоновкой узлов сопряжения пролетных балок моста, концевых балок и конструктивным исполнением ходовой части крана. Примеры компоновок механизма передвижения крана грузоподъемностью 50 т и стыка балок приведены на рис. 10.7 и 10.8.
В качестве примеров на рис. 7.1 показана схема исполнения моста крана грузоподъемностью 150/32 т среднего режима работы пролетом 22 м завода Сибтяжмаш, а на рис. 7.2 и 7.3 – компоновочные схемы приводов механизма передвижения крана.
Решающее значение при компоновке моста имеет схема ходовой части крана. Схемы ходовых частей показаны на рис. 7.4.
В выполненных конструкциях краны грузоподъемностью до 50 т включительно имеют 4 ходовых колеса. Краны завода Сибтяжмаш грузоподъемностью 80…120 т со всеми пролетами и грузоподъемностью 160 т при пролете до 16 м имеют 8 колес, грузоподъемностью 160 т при пролете более 16 м и грузоподъемностью 200…320 т со всеми пролетами – 16 колес (рис. 7.4). По действующим нормам база крана В ≥ L /6, где L — пролет крана.
Узел сопряжения пролетных и концевых балок моста должен обеспечить размещение приводов механизмов передвижения крана, возможность монтажа и обслуживания привода, возможность выхода на галерею из кабины машиниста, прочность и надежность соединений пролетных и концевых балок моста.
У четырехколесных кранов колесные установки монтируются непосредственно в концевых балках моста, у 8‑ и 16‑колесных кранов – в сварных или литых балансирах, которые, в свою очередь, монтируются на металлоконструкции моста, что определяет как конструкцию концевых балок, так и конструкции узлов сопряжения пролетных и концевых балок моста.
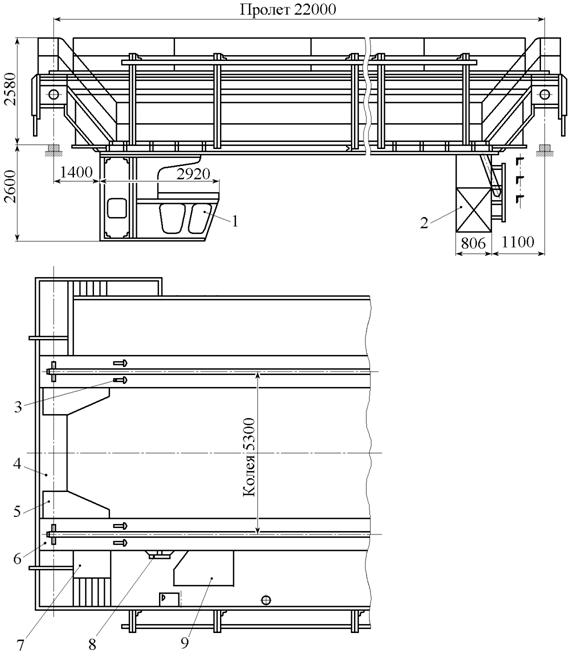Рис. 7.1. Мост крана общего назначения грузоподъемностью 150/32 т:
1 — кабина машиниста; 2 — люлька осмотра троллей; 3 — тупиковые упоры; 4 — концевая балка; 5 — косынка соединения балок моста; 6 — пролетная балка; 7 — люк выхода из кабины на мост; 8, 9 — площадки привода механизма передвижения
|
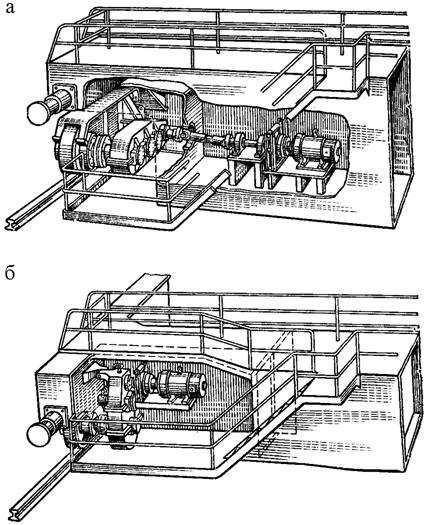Рис. 7.2. Привод механизма передвижения крана
|
Рис. 7.3. Привод ходового колеса механизма передвижения крана большой грузоподъемности
|
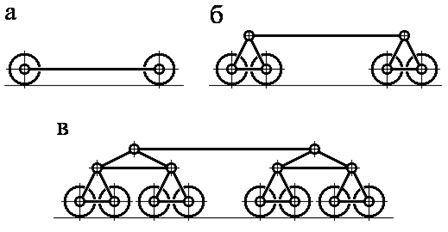Рис. 7.4. Схемы расположения колес
|
Основные параметры приводов механизмов передвижения [2, 10] двухбалочных кранов общего назначения грузоподъемностью 5…320 т режимных групп А4, А5 приведены в табл. 7.1.
| Таблица 7.1 Параметры приводов механизмов передвижения кранов грузоподъемностью 5…320 т | ||||||
| Грузоподъемность крана, т | Электродвигатель | Редуктор | Тормоз | Диаметр ходового колеса, мм | Число колес | |
| общее | приводных | |||||
| МТ 111-6 | Ц2-250 | ТТ-160 | ||||
| МТВ 112-6 | Ц2-300 | ТТ-160 | ||||
| 12,5 | МТВ 211-6 | Ц2-300 | ТТ-200 | |||
| МТВ 211-6 | Ц2-300 | ТТ-200 | ||||
| МТВ 311-6 | Ц2-400 | ТТ-250 | ||||
| МТВ 411-6 | Ц2-500 | ТТ-250 | ||||
| МТ 211-6 | ВКУ-750 | ТКГ-200 | ||||
| МТ 112-6 | ВКУ-750 | ТКГ-200 | ||||
| 320 при пролете до 25 м | МТ 112-6 | ВКУ-750 | ТКГ-200 | |||
| 320 при пролете более 25 м | МТВ 312-6 | ВКУ-750 | ТКГ-200 |
Ходовые колеса кранов унифицированы, их основные присоединительные размеры приведены на рис. 7.5 и в табл. 7.2.
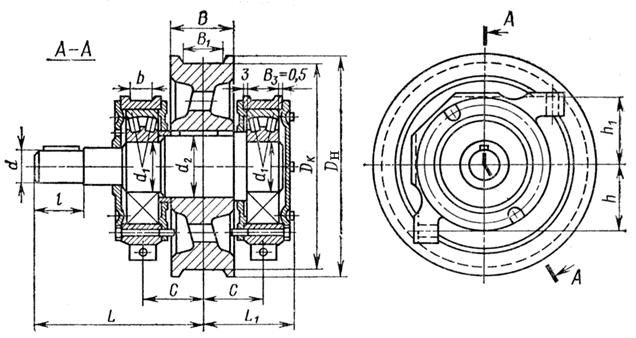Рис. 7.5. Колесо крановое на угловых буксах
|
| Таблица 7.2 Размеры крановых колес типа I | ||||||||||||||||
| D К | D Н | d | d 1 | d 2 | B | B 1 | b | b 1 | L | L 1 | l | h | h 1 | C | Номер подшипника | Масса, кг |
| 238,5 | ||||||||||||||||
Далее рассматриваются возможные варианты компоновки узлов сопряжения балок моста и приводов механизмов передвижения.
7.2. Четырехколесные краны грузоподъемностью 5…50 т
7.2.1. Концевые балки
Типовая схема конструктивного исполнения концевых балок показана на рис. 7.6, установка колес в концевых балках традиционной конструкции — на рис. 7.7.
| |
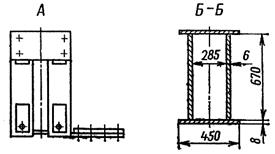
| Рис. 7.6. Концевая балка |
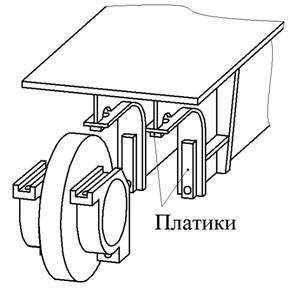
| Рис. 7.7. Установка ходового колеса |
Надбуксовая часть концевой балки представляет собой открытое тонкостенное сечение, подверженное интенсивным изгибающим и скручивающим нагрузкам, и является одним из самых слабых элементов конструкции. Поэтому для обеспечения работоспособности требуется проведение строгого расчета.
Расчетная схема надбуксового участка показана на рис. 7.8.
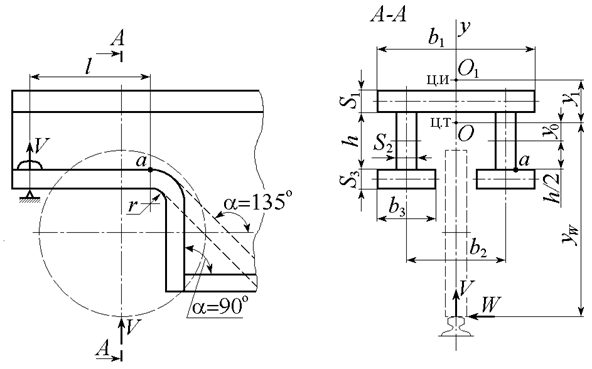Рис. 7.8. Расчетная схема надбуксовой части концевой балки четырехколесного крана
|
Расчетные нагрузки определяются для комбинации II B при расположении тележки с грузом у концевой балки:
V — вертикальная нагрузка на колесо от веса моста, тележки и груза; W — реакция от силы перекоса крана.
Обозначим площади элементов:
F 1= b 1 S 1; F 2= hS 2; F 3= b 3 S 3. (7.1)
Полагая толщину пластин малой по сравнению с их длиной, получим приблизительные геометрические характеристики сечения:
- координату центра тяжести сечения (т. О) относительно середины высоты стенки,
; (7.2)
- моменты инерции сечения при изгибе,
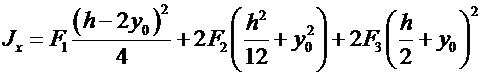; (7.3)
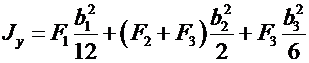; (7.4)
- момент инерции при кручении,
; (7.5)
- координату центра изгиба в горизонтальной плоскости (т. О1) (по аналогии с [20]),
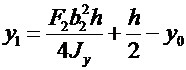. (7.6)
Проверка прочности производится [13] по приведенным напряжениям в месте перехода от прямолинейной к закругленной части нижнего листа (т. а на рис. 7.8) по формуле
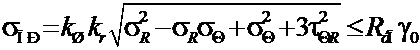, (7.7)
где k Ш — коэффициент формы шва, который учитывается только при расчетах на выносливость; при тавровом соединении двухсторонним швом (рис. 9.3, а) k Ш=1,0, при тавровом соединении односторонним швом (рис. 9.3, б) k Ш=1,4.