В одной культуре определённые числа могут считаются счастливыми, в других — наоборот, несчастными. Согласно китайскому поверию, каждому числу присущи своё индивидуальное значение, влияние и сила.
Чётные числа считаются в Китае более счастливыми, чем нечётные, поскольку чётные числа ассоциируются с энергией живых, а нечётные — энергией умерших. Исключение — четвёрка («4»): хоть это и чётное число, но оно, как и в Японии (см. выше), созвучно с иероглифом «смерть». Типичный китаец вряд ли пожелал бы стать владельцем квартиры №4, телефонного номера, оканчивающегося на четвёрку, или автомобиля, в номере которого присутствует цифра 4. Китайцы всячески избегают четвёрку.
Число 14 тоже считается негативным в плане энергетики, а также 13, так как сумма его разрядов сводится к цифре четыре: 1 + 3 = 4. Во многих бизнес-центрах, принадлежащих китайцам, которые исповедуют даосизм, в лифтах, как правило, отсутствуют соответствующие этажи; чаще всего они заменены следующими по счёту цифрами. В Гонконге введено за правило пропускать вообще все негативные номера этажей.
1.5. Значения каждой из цифр от 1 до 9 в Китае:
«1 » — мужественность, новое начало, одиночество.
«2 » — символизирует пары, считается благополучным числом. У китайцев даже есть выражение: «Всё хорошее удваивается». Двойка — однозначно положительная цифра для китайцев.
«3 » — ассоциируется с рождением. В целом благоприятная цифра.
«4 » — наиболее несчастливое, негативное число для китайцев (причина рассмотрена выше).
«5 » — символизирует 5 элементов: дерево, огонь, землю, металл и воду, которые имеют отношение к «небесным стволам» китайского циклического календаря. Именно поэтому пятёрка («5») — позитивная цифра, хоть и нечётная.
«6 » — ассоциируется у китайцев со счастьем и бизнесом, почитается как очень счастливое число.
«7 » — ассоциируется с чувством единства, но является нечётным, и поэтому рассматривается китайцами и как счастливое, и как несчастливое число; а вот японцы семёрку любят гораздо больше.
«8 ». Восьмёрка — наиболее счастливое число для всех китайцев. Звучит, как «богатство» и «процветание». Китайцы очень часто готовы платить огромные деньги за номер телефона, номер машины или номер квартиры, в которых присутствует цифра 8 (а также 9). Кроме того, форма восьмёрки напоминает знак бесконечности, и поэтому у китайцев восьмёрка ассоциируется с никогда не заканчивающимся потоком денег, которые поступают в бизнес или человеку, в зависимости от того, где эта цифра используется.
Показательный пример: летние Олимпийские игры 2008 года в Пекине были объявлены открытыми 08.08.08 в 08:08.08 (PM). Шесть восьмёрок! Китайцы верили, что это принесёт удачу их национальной команде (так и произошло: у Китая было больше всего золотых медалей и, как следствие, 1-е место в неофициальном командном зачёте).
«9 » — ассоциируется с бессмертием, долгожительством, счастьем; также очень счастливое число. Самой счастливой комбинацией считается 98.
Арифметические операции
Вероятно, уже со времени Сражающихся царств все фундаментальные арифметические действия (сложение, вычитание, умножение и деление) выполнялись с помощью счетных палочек на счетной доске и с использованием системы поместного значения, в которой пробелы были оставлены там, где мы помещаем нули. Хотя иероглифы в китайском письме традиционно писались сверху вниз, цифры на счетной доске всегда размещались по горизонтали слева направо. Сложение целых чисел и дробей обозначалось разными иероглифами – «бин» и «хэ». Вычитание обозначалось иероглифом «цзянь». Умножение считалось упрощенным сложением множества слагаемых. Данную операцию обозначал иероглиф «чэн». Его исходное значение – «упряжка», «колесница», «ехать на колеснице». Отсюда множители могли мыслиться как упряжка лошадей, управляемая возничим. Деление («чу», исходное значение «удалять») рассматривалось китайцами как упрощенное вычитание или как перевернутое умножение. Делитель назывался «фа» (букв. «норма») а делимое – «ши» (букв. «полнота»). Таблицы деления (использующие слова) были обычны начиная с эпохи Сун.
Действия по китайскому методу вычислений на счетной доске начинаются с высших разрядов, а затем поэтапно переходят на более низшие. Такой порядок предполагал корректирование промежуточных результатов, что было легко, поскольку достигалось перекладыванием счетных палочек. После каждого этапа предыдущий промежуточный результат заменялся на новый вплоть до получения окончательного результата. Это делало невозможным непосредственную проверку всей последовательности действий.
Ввиду простоты сложения и вычитания в математических текстах не приводятся правила их выполнения. Первое описание правил умножения и деления дано в книге Сунь-цзы «Сунь-цзысуаньцзин». Осуществление этих действий проводилось в трех позициях («вэй») на счетной доске – в верхней («шан»), средней («чжун») и нижней («ся»). При умножении множимое помещалось в верхней позиции, множитель – в нижней и их произведение – в средней. При делении делимое располагалось посередине, делитель – внизу, а их частное – вверху.
| Позиция | Умножение | Деление |
| Верхняя | Множимое | Частное |
| Средняя | Произведение | Делимое |
| Нижняя | Множитель | Делитель |
Вот один из примеров Сунь-цзы на умножение (рис.8).
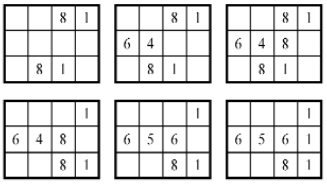
Рис.8
Изложение правила умножения Сунь-цзы начинает с указания на необходимость установить множимое и множитель таким образом, чтобы между их разрядами было прямое соответствие, чтобы они «друг на друга взирали» (сянгуань). Правда, вслед за этим, судя по приводимому Сунь-цзы примеру умножения 81 на 81, множитель передвигается вправо так, чтобы его низший разряд находился под высшим разрядом множимого (рис. 8). Затем надо осуществить ряд операций, которые лучше рассмотреть на примере Сунь-цзы. Первая их серия следующая: число в высшем разряде множителя (8) умножается на число из аналогичного разряда множимого (8); произведение (64 сотни) записывается в средней позиции; число в низшем разряде множителя (1) умножается на число из высшего разряда множимого (8); получившееся произведение (8 десятков) складывается с предыдущим произведением (648 десятков). Вторая серия операций начинается с перемещения («туй», буквально «отступать») множителя на одну клеточку вправо и удаления у множимого использованного высшего разряда. Затем число из высшего разряда множителя (8) умножается на число, оставшееся от множимого (1); получается 8 десятков, которые складываются с предыдущим результатом (80 + 6480 = 6560). Наконец на остаток множимого (1) умножается число из низшего разряда множителя (1); получается единица, которая складывается с предыдущим результатом, что дает число 6561.
Поскольку деление обратно умножению, Сунь-цзы не видит надобности в описании правила выполнения этого действия, а ограничивается примерами. Для начала приводится пример правильного соотнесения разрядов конкретных делителя и делимого – 6 и 100. Перед началом операций надо «выдвинуть» («цзинь») делитель под самый высокий разряд и посмотреть, возможно ли деление. В разряде сотен стоит число, меньшее делителя. Значит, деление не возможно, и нужно отступить на одну клеточку вправо. Деление 10 на 6 возможно.
Еще дается пример деления 6561 на 9 (рис. 9). Первая позиция делителя будет соответствовать сотням делимого. Делится 65 сотен на 9. Помимо остатка получатся 7 сотен, которые помещаются в верхнюю позицию. Из делимого вычитается 63 сотни (= 9 х 7 сотен). В средней позиции получается 261. Делитель перемещается в ячейку справа. Если разделить 26 десятков на 9, то помимо остатка получится 2 десятка, которые записываются в позиции частного, суммируясь тем самым с 7 сотнями. Из числа 261 вычитается 18 сотен (= 9 х 2 десятка). Получается число 81, которое записывается в средней позиции. После этого делитель передвигается еще на одну ячейку вправо. Совершается деление остатка делимого на делитель. Получается число 9, которое суммируется с числом в верхней позиции, что дает результат 729.
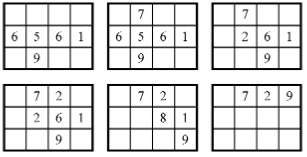
Рис.9
При рассмотрении операции деления Сунь-цзы вводит важное дополнительное правило, касающееся деления с остатком. В этом случае последняя комбинация палочек на счетной доске должна рассматриваться как «запись» частного, состоящего из целого числа и дроби: делитель берется в качестве знаменателя, а остаток делимого – в качестве числителя. Например, при делении 100 на 6 получится 164/6 (рис. 10).