- 1. Следующие задачи нелинейного программирования:
а) Привести к стандартному и унифицированному виду (прямые ограничения представлены в виде функциональных).
б) Изобразить допустимое множество и линии уровня целевой функции. Определить, выполняются ли условия теоремы Вейерштрасса о существовании решения?
в) Вычислить и изобразить на рисунке направления градиентов целевой функции и функций, описывающих активные ограничения, в указанных и угловых точках.
г) На рисунке проверить выполнение условий Якоби и Куна-Таккера в указанных и угловых точках.
д) В точках, где выполняются условия Якоби и Куна-Таккера, разложить градиент целевой функции по градиентам функций, задающих активные ограничения в этих точках, и найти множители Лагранжа.
е) Изобразить линии уровня целевой функции и проверить наличие или отсутствие в этих точках локального и глобального максимумов.
ж) Оценить графически, существуют ли еще точки, в которых выполняются условия Куна-Таккера, и найти эти точки. Определить (графически) наличие или отсутствие локального максимума в них.
1) 
 , (3/4; 1/4); (1/2; 1/4);
, (3/4; 1/4); (1/2; 1/4);
2)  , (0;1), (2;3);
, (0;1), (2;3);
3)  ; 4)
; 4)  ; 5); 6)
; 5); 6) 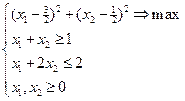 .
.
2. Определить с обоснованием, являются ли множества, заданные указанными ограничениями, выпуклыми и изобразить их.
а) 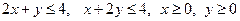 ;
;
б)  ;
;
в)  ;
;
г) 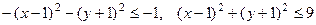 ;
;
д)  ;
;
е)  .
.
3. Определить, будут ли выпуклы (вогнуты) заданные функции на заданных множествах.
а) функция  на E2;
на E2;
б) функция  на E2;
на E2;
в) функция  на E2;
на E2;
г) функция  на E2;
на E2;
д) функция  на множестве
на множестве  =
=  ;
;
е) функция  на квадрате с вершинами
на квадрате с вершинами  ;
;
ж) функция  на множестве
на множестве  ;
;
з) функция  на прямоугольнике с вершинами {(0;0),(1;0),(0;4),(1;4)};
на прямоугольнике с вершинами {(0;0),(1;0),(0;4),(1;4)};
и) функция  на прямоугольнике с вершинами
на прямоугольнике с вершинами
{(1; 1), (1; -1), (-1; 1), (-1; -1)}.
-
- 4. Являются ли следующие задачи задачами выпуклого программирования? Ответ обосновать.
а)  при
при 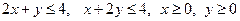 ;
;
б)  при
при  ;
;
в)  при
при  ;
;
г)  при
при  ;
;
д)  при
при  ;
;
е)  при
при  ;
;
ж)  при
при  ;
;
з)  при
при  .
.
5. В следующих задачах нелинейного программирования выполнить следующие задания и ответить на вопросы:
а) Привести задачу к стандартному и унифицированному виду (прямые ограничения представлены в виде функциональных).
б) Изобразить допустимое множество и линии уровня целевой функции. Определить, выполняются ли условия теоремы Вейерштрасса о существовании решения?
в) Является ли данная задача задачей выпуклого программирования?
г) Возможно ли применение теоремы Куна-Таккера в данной задаче? Почему?
д) Рассматривая различные наборы активных ограничений, увеличивая их количество, начиная с нуля, аналитически найти точку, в которой выполняются условия Куна-Таккера. Указать такую точку и продемонстрировать выполнение условий Куна-Таккера на рисунке.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  .
.
6. Фирма производит два вида товаров: А и В. Для производства  единиц товара А и
единиц товара А и  единиц товара В требуется заранее приобрести
единиц товара В требуется заранее приобрести  кг сырья. Из-за ограничений на объем склада количество сырья не должно превышать 2100 кг. Доход от реализации единицы товара А составляет $2000, а от реализации единицы товара В – $1000. Определить план выпуска, максимизирующий доход. Оценить, на сколько изменится доход, если объем склада увеличить на 1 кг.
кг сырья. Из-за ограничений на объем склада количество сырья не должно превышать 2100 кг. Доход от реализации единицы товара А составляет $2000, а от реализации единицы товара В – $1000. Определить план выпуска, максимизирующий доход. Оценить, на сколько изменится доход, если объем склада увеличить на 1 кг.
-
7. Решить задачу
а)  при
при  , x1 ≥0, x2 ≥0, x3 ≥0;
, x1 ≥0, x2 ≥0, x3 ≥0;
б)  при
при  , x1 ≥0, x2 ≥0, x3 ≥0;
, x1 ≥0, x2 ≥0, x3 ≥0;
в)  при
при  , x1 ≥0, x2 ≥0, x3 ≥0.
, x1 ≥0, x2 ≥0, x3 ≥0.
При этом:
1. Проверить, выполняется ли для данной задачи нелинейного программирования условия теоремы Вейерштрасса;
2. Проверить, является ли данная задача задачей выпуклого программирования;
3. Проверить возможность использования условий Куна-Таккера (необходимость и достаточность) в данной задаче;
4. Найти решение рассматриваемой задачи нелинейного программирования на основе проверки выполнения условий Куна-Таккера в градиентной форме для различных наборов активных ограничений;
5. Выписать функцию Лагранжа и условия Куна-Таккера в алгебраической форме с использованием функции Лагранжа; проверить выполнение условий Куна-Таккера в решении, найденном в предыдущем пункте.
1. Фирма производит продукцию трех видов: A, B, C. Для ее изготовления используются оборудование и трудовые ресурсы. Для изготовления единицы продукции A требуется одна единица оборудования в течение одного часа и два человеко-часа трудовых ресурсов, для изготовления единицы продукции B – две единицы оборудования в течение одного часа и один человеко-час трудовых ресурсов, продукции C – одна единица оборудования в течение одного часа и 3 человеко-часа. Прибыль от реализации продукции A и B пропорциональна ее количеству с коэффициентом пропорциональности $10 и $6 соответственно, а вида C – квадратному корню из ее количества с коэффициентом пропорциональности $440. В настоящее время фирма располагает 1210 часами работы оборудования и 2420 человеко-часами трудовых ресурсов в месяц. Определить план выпуска, максимизирующий прибыль. Проанализировать чувствительность максимальной прибыли к константам ограничений на ресурсы.