1. Привести задачи линейного программирования к стандартной и канонической формам:
а) 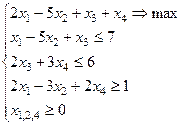 ; б)
; б)  ; в)
; в)  .
.
2. Составить задачи линейного программирования для следующих проблем и решить графически:
а) Озеро можно заселить двумя видами рыб: А и В. В озере имеется два вида пищи: Р1 и Р2. Средние потребности в пище рыбы вида А составляют 0,5 ед. корма Р1 и 1,5 ед. корма Р2 на 1 кг рыбы в день. Потребности в пище рыбы вида В составляют 2 ед. корма Р1 и 1 ед. корма Р2 на 1 кг рыбы в день. Ежедневный запас пищи поддерживается на уровне 500 ед. Р1 и 900 ед. Р2. Каковы должны быть массы отдельных видов рыб для того, чтобы максимизировать общую массу рыбы в озере?
б) Имеется 2 вида кормов А и B, которые можно купить по ценам $8 и $10 за килограмм. В одном килограмме корма А содержится 50 г питательного вещества М и 100 г питательного вещества N. Для корма В соответствующие цифры составляют 100 г и 50 г. Сколько требуется закупить кормов А и B, чтобы общее количество питательных веществ М и N составляло не менее 4 кг и 5 кг соответственно, а расходы были минимальны? Вычислить минимальные расходы.
в) Фабрика по производству мороженого может выпускать два сорта мороженого: молочное и сливочное. При производстве мороженого используют три вида сырья: молоко, дешевые наполнители и дорогие наполнители, запасы которых составляют 5 т, 3 т и 5,7 т соответственно. Известны удельные затраты сырья для каждого из сортов и цены продукции. Для молочного мороженого они составляют 0,5 кг,0,1 кг и 0,4 на 1 кг мороженого, а для сливочного – 0,2 кг, 0,3 и 0,5 кг на 1 кг мороженого. Цена молочного мороженого составляет 200 рублей за 1 кг, а сливочного – 300 рублей за 1 кг. Требуется построить план производства, который обеспечивает максимум дохода, и найти оптимальный доход.
3. Составить математические задачи оптимизации для следующих проблем и решить их. Дать интерпретацию оптимальных значений двойственных переменных. Провести анализ чувствительности оптимального значение критерия по отношению к изменениям объемов используемого сырья. Найти пределы, в которых данные значения двойственных переменных могут быть использованы для расчета влияния изменения объемов сырья.
а) Имеется два вида сырья: S1 и S2 в количествах 800 и 1400 кг. Можно изготовить три вида продукции: Р1, Р2 и Р3. Затраты сырья на кг продукции составляют соответственно: 4;2;5 и 2;6;5. Цена готовых изделий: $8; $14; $10. При планировании максимизируется доход.
б) На заводе имеется запас олова и свинца в объеме 3 тонн и 5 тонн соответственно. Из этих металлов завод может изготовить три вида сплавов этих металлов: с содержанием олова 20 %, 30 % и 50 %. Сплав первого вида завод может реализовать по цене $80 за кг, второго – $140, третьего – $200. Составить план производства, максимизирующий доход, и вычислить этот доход.
-
в) Фирма по производству творожной пасты может выпускать два сорта пасты, используя три вида сырья – молоко, наполнители и специальные добавки. Затраты молока на килограмм пасты первого вида составляют 0.1 кг, а второго вида – 0.5 кг. Затраты наполнителей на килограмм пасты первого вида составляют 0.2 кг, а второго вида – 0.1 кг. Наконец, затраты добавок на килограмм пасты первого вида составляют 0.1 кг, а при производстве второго вида пасты не используются. Запасы молока составляют 350 кг, наполнителей – 160 кг, добавок – 60 кг. Цена 1 кг первого вида пасты составляет 200 рублей, а второго вида – 300 рублей. Найти план производства, максимизирующий доход от продажи творожной пасты, и соответствующее значение дохода. Записать двойственную задачу, найти ее решение и дать интерпретацию двойственным переменным. Провести анализ чувствительности к малым изменениям запасов.
4. При каких значениях параметра задача линейного программирования 
- а) не имеет решений; б) имеет единственное решение; в) имеет бесконечное множество решений? Найти эти решения.
5. Для каждой из следующих задач ЛП перейти к двойственной задаче, решить ее графически и найти решение исходной задачи.
а)  ; б)
; б)  .
.