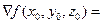Контрольная работа
Теоретические вопросы
Вопрос 1 (1 балл)
Отметьте (галочкой в отведенном поле) все требования, входящие в систему достаточных условий существования единственной точки глобального максимума функции f на множестве Х. Избыточныхтребований не указывать.
 |
1. 
Выпуклость множества Х 2. Ограниченность множества Х
3. Замкнутость множества Х 4. Открытость множества Х
5.Непустота множества Х 6. Строгая вогнутость функции f
7. Непрерывность функции f 8. Строгая выпуклость функции f
 |
Оценка: не заполнять!
Вопрос 2 (1 балл)
Отметьте (галочкой в отведенном поле) все требования, входящие в систему достаточных условий строгой выпуклости дважды непрерывно-дифференцируемой функции f на множестве 
с непустой внутренностью. Избыточных требований не указывать.
 | |||
 | |||
1. Выпуклость множества Х 6. Положительная определенность матрицы Гессе на Х
2.Непустота множества Х 7. Неотрицательная определенность матрицы Гессе на Х
3. Ограниченность множества Х 8. Отрицательная определенность матрицы Гессе на Х
4. 
Замкнутость множества Х 9. Неположительная определенность матрицы Гессе на Х
5. Открытость множества Х 10. Знаконеопределенность матрицы Гессе на Х
 |
Оценка: не заполнять!
Вопрос 3 (1 балл)
Известно, что дифференцируемая функция f задана на множестве 
, 
дифференцируемы на 
, причем в точке 
выполняется условие Куна-Таккера, но не выполняется условие Якоби. Другой информации нет. Какие выводы из перечисленных ниже можно сделать в этой ситуации? Отметьте (галочкой в отведенном поле) эти выводы.
-
В точке имеет место локальный максимум -
В точке имеет место глобальный максимум -
В точке нет локального максимума -
В точке может быть, но может и не быть локального максимума -
Такая ситуация невозможна
 |
Оценка: не заполнять!
Вопрос 4 (2 балла)
Известно, что в задаче нелинейного программирования 
функция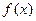 
дифференцируема и вогнута на , а функции 
, 
дифференцируемы и выпуклы на , причем в точке , 
, выполняется условие Куна-Таккера.Другой информации нет. Какой из перечисленных ниже выводов можно сделать в данной ситуации? Отметьте (галочкой в отведенном поле) этот вывод.
-
В точке имеет место локальный максимум, не являющийся глобальным - В точке имеет место глобальный максимум
- В точке нет локального максимума
- В точке может быть, но может и не быть локального максимума
- Такая ситуация невозможна
 |
Оценка: не заполнять!
Задача 1 (5 баллов)
Фирма наращивает три вида своих производственных мощностей. Получаемая ею прибыль 
определяется по формул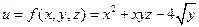е 
, где 
– нарастающие итоги средств, вложенных ею в указанные производственные мощности, которые предполагаются неамортизируемыми. В настоящее время накопленные фирмой инвестиции составляют 
единицу, 
единицу, 
единицу. Руководством фирмы было принято решение вложить имеющиеся относительно небольшие средства в развитие указанных мощностей в пропорции 1:5:1.
Оцените, будет увеличиваться или уменьшаться прибыль фирмы при таком распределении ресурсов в ближайшей перспективе.
В каком соотношении следовало бы вкладывать средства в развитие указанных мощностей, чтобы в ближайшей перспективе прибыль фирмы возрастала наиболее быстрыми темпами?
Этапы решения
1.1. (1 балл) Вычислить градиент функции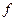 
в общем виде
1.2. (1 балл) Вычислить градиент функции 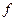в заданной точке
|
1.3. (2 балла) Вычислить производную по направлению
|
(1 балл) Указать правильный ответ
 |
Будет повышаться Будет понижаться
Оптимальные пропорции вложения средств: 
Оценка: не заполнять!
Задача 2 (10 баллов)
Является ли функция 
выпуклой (вогнутой) на множестве 
?
Этапы решения
2.1. (1 балл) Выписать матрицу Гессе
 |
2.2. (3 балла) Выписать в терминах главных миноров матрицы Гессе необходимые и достаточные условия выпуклости и вогнутости дважды дифференцируемой функции двух переменных на выпуклом множестве 