 |  |
2.3. (4 балла) Изобразить области выпуклости и вогнутости заданной функции в пространстве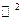 
, а также заданное множество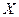 
2.4. (1 балл) Обосновать выпуклость множества 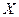аналитически
 |
2.5. (1 балл) Отметить галочкой правильный ответ
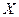Выпукла на Вогнута на 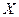Не выпукла и не вогнута на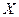
 |
Оценка: не заполнять!
Задача 3 (12 баллов)
Фирма может производить три вида продукции: А, В и С. Для производства 
единиц продукции А,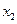 
единиц продукции В и 
единиц продукции С требуется 
единиц ресурса, запасы которого равны 6 единицам. Прогнозируемая цена на рынке для продукции вида А составляет 1 тыс. рублей, вида В – 2 тыс. рублей, вида С – 2 тыс. рублей.
Составить оптимальный план производства продукции, максимизирующий доход от ее продажи на рынке, в предположении полного расходования запасов ресурса. Как изменится максимальный доход, если запас ресурса увеличить на 0,01 единицы?
Решить задачу методом Лагранжа как классическую задачу математического программирования с оценкой чувствительности (решения, не соответствующие физическому смыслу переменных, отбросить в конце решения задачи).
Этапы решения
3.1. (1 балл) Составить математическую модель задачи
3.2. (1 балл) Проверить выполнение условия Якоби
Вывод
3.3. (1 балл) Выписать функцию Лагранжа
 |
3.4. (1 балл) Выписать необходимые условия первого порядка
3.5. (1 балл) Найти стационарные точки
Вычисления
Стационарные точки
3.6. (1 балл) Выписать окаймленную матрицу Гессе
 |
3.7. (3 балла) Путем исследования окаймленной матрицы Гессе установить наличие и вид локальных экстремумов в найденных стационарных точках
Вычисления
Выводы
3.8. (2 балла) Найти решение задачи (точку глобального максимума, максимальное значение целевой функции) с обоснованием
Оптимальная точка
(1 балл)
Максимальное значение
 |
Обоснование
(1 балл)
3.9. (1 балл) Оценить, как изменится оптимальный доход, если запас ресурсов увеличить на 0,01 единицы
 |
Вычисления
Вывод
|
Оценка: не заполнять!
Задача 4 (18 баллов) Исследовать задачу нелинейного программирования
при 
Этапы решения
4.1. (1 балл) Привести задачу к стандартному видуи к виду, удобному для графического анализа (прямые ограничения представлены в форме функциональных)
Стандартный вид задачи Вид задачи, удобный для графического анализа
 | |||
 | |||
4.2. (2 балла) Изобразить допустимое множество и линии уровня целевой функции
4.3. (1 балл) Обосновать существование или отсутствие решения задачи
 |
4.4. (1 балл) Является ли данная задача задачей выпуклого программирования? Ответ обосновать и подтвердить расчетами.
4.5. (1 балл) Вычислить градиенты целевой функции и всех функций, описывающих ограничения
4.6. (1 балл) Найти точки, в которых не выполняется условие Якоби, или обосновать их отсутствие
4.7. (4 балла) Найти графически все точки, в которых выполняются условия Куна-Таккера (изобразить направления градиентов на рисунке из п.4.2 и обозначить их), вычислить их координаты и выписать разложения градиента целевой функции по градиентам функций, описывающих активные ограничения
| Точка (координаты) | Разложение (без вычисления коэффициентов) |
4.8. (2 балла) На основании известных Вам необходимых или достаточных условий (а где невозможно, – на основе графического анализа) сделать вывод о наличии или отсутствии локального максимума во всех угловых точках, а также в других точках, в которых выполняется условие Куна-Таккера
| Точка | ||||||
| Наличие локального максимума (+), отсутствие (–) |
4.9. (4 балла) С помощью функции Лагранжа проверить аналитически выполнение условий Куна-Таккера в точке (3;0)
а) Выписать функцию Лагранжа для данной задачи (1 балл)
б) Выписать систему условий Куна-Таккера для задачи с двумя переменными и 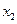и двумя функциональными ограничениями, используя символ функции Лагранжа 
(1 балл)
 |
в) Выписать систему условий Куна-Таккера для заданной точки, решить ее и сделать вывод
(2 балла)
 | |||
 |
Указать верный вывод: Условие Куна-Таккера выполняется
Условие Куна-Таккера не выполняется
4.10. Найти (с обоснованием) глобальный максимум (1 балл)
| 
| Обоснование |
Оценка: не заполнять!
Экзаменационная работа
Задача 1. (7 баллов). Некий гражданин хочет извлечь доход из имеющейся у него суммы в 100 тыс. руб. Он рассматривает три возможности – положить все деньги в банк на срочный вклад, или вложить их в инвестиционный фонд, или приобрести на них акции. Доход от этих действий, однако, не во всех случаях известен заранее, поскольку зависит от мировой цены на нефть. В то время как банк гарантирует 5 % годовых при любых ценах на нефть, доход от вложений в инвестиционный фонд зависит от этих цен: при высоких ценах он составит 25 % от вложенной суммы за год, при средних ценах составит 15 % за год, а при низких ценах будут иметь место потери, которые составят 10 %. В случае приобретения акций, доходы составят 40 % за год при высоких ценах на нефть и 1 % при средних ценах, а при низких ценах на нефть будут иметь место потери в 20 %. Найти максимальную гарантированную оценку прибыли и гарантирующее решение, а также наилучшие решения по критериям Байеса-Лапласа (равной вероятности), Гурвича, Сэвиджа (минимизации сожалений).
Этапы решения
1 балл 1.1. Формализация задачи
Обозначив возможные решения через x 1, x 2 и x 3, а возможные значения неопределенности через ξ 1, ξ 2 и ξ 3, составить матрицу доходов (платежную матрицу) aij= f (xi, ξj)
| ξ 1 | ξ 2 | ξ 3 | |||||
| x 1 | |||||||
| x 2 | |||||||
| x 3 |
|
|
и гарантирующего решения 
для матрицы доходов общего вида (f (xi, ξj) = aij, i = 1,… n; j = 1,… m), а также найти такой результат и такое решение для матрицы п. 1.1.
 | |||
 | |||
= =
 |  | ||
= =
|
|
| |||
| |||
= =
| |||
 | |||
= =
1 балл 1.4. Дать определение наилучшего решения по критерию Гурвичаи найти такое решение с параметром 
для матрицы п. 1.1.
|
|
| |||
| |||
= =
| |||
| |||
= =
2 балла 1.5. Дать определения наилучшего решения по критерию Сэвиджа и найти такое решение для матрицы п. 1.1.
|
|
| |||
| |||
= =
| |||
| |||
= =
|
(не заполнять!!!)
Задача 2. (8 баллов).
Фабрика по производству мороженого может выпускать пять сортов мороженого. При производстве мороженого используется два вида сырья: молоко и наполнители, запасы bj, j =1,2, которых точно известны. Планирование производства осуществляется в условиях неопределенности – неточно известны удельные затраты сырья 
, j =1,2, i =1,2,..,5, а также цены 
продукции, i =1,2,..,5. Для неопределенных параметров известны диапазоны их возможных значений (см. таблицу). Требуется построить план производства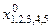 
, который был бы выполним при любых значениях неопределенных параметров и обеспечивал максимум гарантированной оценки дохода в условиях, когда информация о связях между неопределенными параметрами отсутствует.
| Объемы производства |
|
|
| 
| 
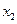
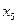
| bj - запасы сырья |
 – удельные затраты сырья 1
| 0,8 - 1 | 1,8 - 2 | 5 - 6 | 2,5 - 3 | 2,8 - 3 | 4 000 |
 – удельные затраты сырья 2
| 0,7 - 1 | 6 - 7 | 1,7 - 2 | 10 - 12 | 4 - 5 | 2 000 |
 – цены продукции
| 4 - 5 | 14 - 15 | 12 - 13 | 18 - 20 | 15 - 16 |
Этапы решения
1 балл 2.1. Сведение к детерминированной задаче линейного программирования
1 балл 2.2. Запись двойственной задачи
4 балла 2.3. Графическое решение двойственной задачи
2 балла 2.4. Решение прямой задачи (с обоснованием и проверкой оптимальности)
Ответ: =; =.
|
(не заполнять!!!)
Задача 3. (10 баллов).
В задаче двухкритериальной максимизации множество допустимых решений задается неравенствами 
и 
, а критерии заданы соотношениями 
. Отклонение от целевого множества задается функцией
.
ЛПР задал целевую точку 
=(3,4). Требуется:
- найти и изобразить множество достижимых критериальных векторов Z, его паретову границу P(Z) и идеальную точку 
;
- изобразить целевое множество G;
- изобразить линии уровня функции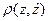 
; графически решить задачу нахождения достижимой точки 
, дающей минимум отклонения от целевого множества;
- аналитически записать задачу минимизации отклонения от целевой точки в виде задачи линейного программирования.
Этапы решения
1 балл 3.1. Изобразить множество допустимых решений и найти его вершины.
Вершины множества допустимых решений:
 |
3 балла 3.2. Найти образы вершин в пространстве критериев; найти и изобразить множество достижимых критериальных векторов Z, его паретову границу P(Z) и идеальную точку z*.
Вершины множества достижимых критериальных векторов:
 |
Множество достижимых критериальных векторов, его паретова граница P(Z) и идеальная точка z*
|
|
4 балла 3.3. Изобразить целевое множество G, линии уровня функции 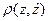и множество Z; графически решить задачу нахождения достижимой критериальной точки , дающей минимум отклонения от целевого множества.
<
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-02 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |