Все первичные погрешности, возникающие при механической обработке на станках можно представить как случайные и систематические.
Систематические погрешности (упругие отжатия, тепловые деформации, размерный износ и другие) возможно прогнозировать по соответствующим аналитическим и эмпирическим зависимостям.
Случайные погрешности (неравномерность снимаемого припуска, разброс по твердости материала обрабатываемой партии и другие) возможно учитывать лишь на основе методов теории вероятности и математической статистики.
В технологии машиностроения нашли применение следующие законы распределения, учитывающие возникающие погрешности:
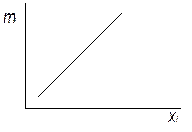
| Закон нормального распределения (распределение Гаусса); | Закон равномерного возрастания, |
| 
|
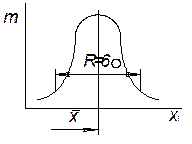
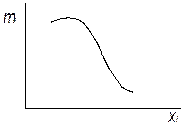
| Закон распределения Симпсона (закон треугольника); | Закон эксцентриситета |
| 
|
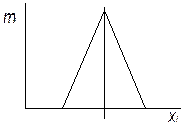
| Закон равной вероятности | |
| |
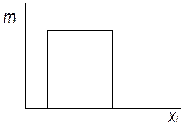
| Рисунок 4.1. Примеры основных законов распределения |
В практике может наблюдаться также и композиция (сочетание) различных законов распределения. Но чаще всего имеет место нормальный закон распределения.
Точечные и точностные диаграммы.
Если технологический процесс или операция являются достаточно стабильными и, влияние всех первичных погрешностей име ет примерно один порядок - для учета и анализа наилучшим образом подходит нормальный закон распределения (закон Гаусса), описывающий поведения различных случайных величин, к которым в совокупности может быть отнесен в том числе и размер детали после механической обработки.
Наиболее простым подходом к оценке точности обработки является подход онованный на использовании точечных или точностных диаграмм.
|
|
В этом случае, по оси абсцисс показывают № измерения (или № измеренной детали), а по оси ординат - значение контролируемого параметра (фактический размер соответствующей детали); также показывают верхнюю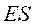 
и нижнюю 
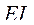границы поля допуска.
|
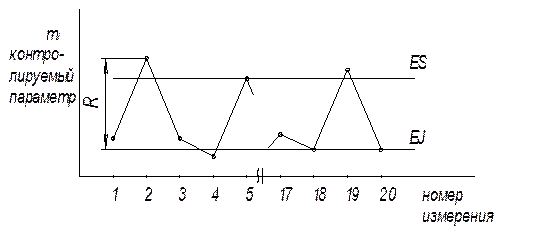
| Рисунок 4.2.Точечная диаграмма |
В том случае, если на одном графике приведены несколько точечных диаграмм, тогда ее называют точностной, так как она периодически (через определенные интервалы времени) дает информацию о фактической точности. Величина объема выборки для точечных диаграмм - не превышает 20 измерений (обычно до 7-10).
Закон Гаусса.
При анализе технологических процессов по точности изготовления деталей допуск по чертежу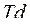 
сравнивается с полем рассеяния 
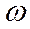. Величина же поля рассеивания зависит от вида закона распределения.
|
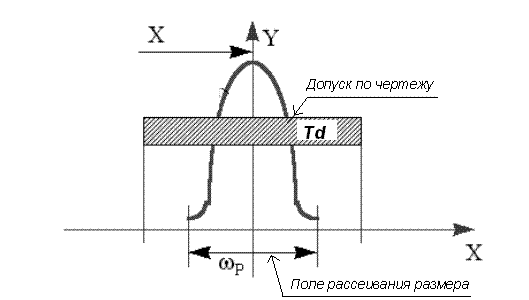
| Рисунок 4.3 Схема нормального распределения и поле допуска на выдерживаемый размер |
Законы распределения характеризуют плотностью распределения вероятностей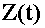 
и параметрами распределения: средним значением 
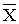и среднеквадратическим отклонением, обозначаемым через 
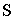(или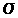 
).
Плотность вероятностей для нормального распределения описывается уравнением Лапласа:
,
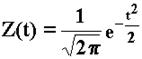где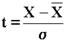 
- параметр распределения;
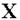- переменная (случайная) величина;
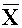- среднеарифметическое отклонение (центр группирования);
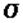- среднеквадратичное отклонение случайной величины;
|
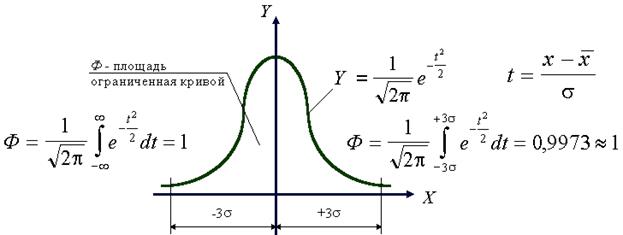
| Рисунок 4.4 Параметры нормального закона распределения |
Величину площади, ограниченной кривой нормального распределения и концами отрезка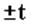 
, можно определить по формуле:
|
|
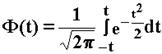- интеграл (функция) Лапласа
Площадь, ограниченная кривой плотности распределения и осью абсцисс, равна:
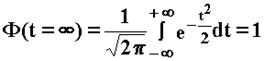
Кривая нормального распределения асимптотически приближается к оси абсцисс. Однако на расстоянии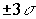 
от вершины кривой ее ветви так близко подходят к оси абсцисс, что в этих пределах находится 99,73% площади, ограниченной кривой и осью абсцисс:
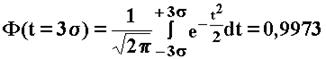
При практическом использовании нормального распределения считают, что вся площадь сосредоточена на расстоянии 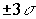. При этом допускается погрешность равная 0,27%.
Тогда поле рассеивания будет равно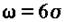 
, то есть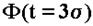 
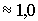(или 100%).