1. n – мерные векторные пространства
Упорядоченная совокупность 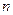 действительных чисел, записанных в виде
действительных чисел, записанных в виде 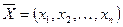 , называется
, называется 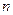 – мерным вектором, где
– мерным вектором, где 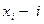 -я компонента. Два
-я компонента. Два 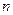 –мерных вектора
–мерных вектора 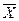 и
и 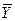 равны тогда и только тогда, когда равны их соответствующие компоненты:
равны тогда и только тогда, когда равны их соответствующие компоненты: 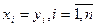 .
.
Операции над 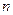 –мерными векторами
–мерными векторами
Пусть 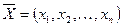 и
и 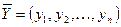 , тогда
, тогда
1) 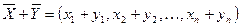 – сложение векторов;
– сложение векторов;
2) 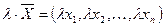 – умножение вектора на число.
– умножение вектора на число.
Операции 1–2 называются линейными и удовлетворяют следующим свойствам:
1) 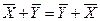 – коммутативность;
– коммутативность;
2) 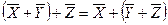 – ассоциативность;
– ассоциативность;
3) 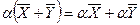 – дистрибутивность;
– дистрибутивность;
4) существует нуль–вектор 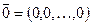 такой, что
такой, что 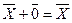 ;
;
5) для любого 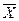 найдется противоположный
найдется противоположный 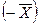 , такой, что
, такой, что 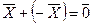 .
.
Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее свойствам 1–5, называется векторным пространством. Если под 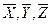 рассматривать объекты любой природы (например алгебраические многочлены степени не выше
рассматривать объекты любой природы (например алгебраические многочлены степени не выше 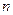 ), то соответствующее множество элементов называется линейным пространством. Линейное пространство
), то соответствующее множество элементов называется линейным пространством. Линейное пространство 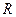 называется
называется 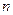 – мерным, если в нем существует
– мерным, если в нем существует 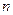 линейно независимых векторов, а любые
линейно независимых векторов, а любые 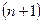 векторов уже линейно зависимы.
векторов уже линейно зависимы.
Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов, т.е. 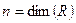 . Совокупность
. Совокупность 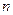 линейно независимых векторов
линейно независимых векторов 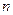 –мерного пространства
–мерного пространства 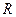 называется базисом.
называется базисом.
Замечание. Векторы 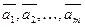 пространства
пространства 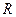 называются линейно зависимыми, если найдутся такие числа
называются линейно зависимыми, если найдутся такие числа 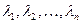 , неравные одновременно нулю, что
, неравные одновременно нулю, что
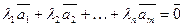 . .
| (18) |
В противном случае векторы 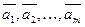 являются линейно независимыми, т.е. равенство (18) выполняется только при
являются линейно независимыми, т.е. равенство (18) выполняется только при 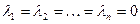 .
.
Любой вектор 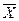 линейного пространства
линейного пространства 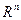 можно представить и при том единственным способом в виде линейной комбинации векторов базиса. Пусть
можно представить и при том единственным способом в виде линейной комбинации векторов базиса. Пусть 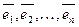 образуют базис в
образуют базис в 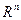 , тогда
, тогда 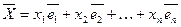 называется разложением вектора
называется разложением вектора 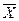 по базису
по базису 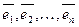 , а числа
, а числа 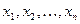 – координаты вектора относительно этого базиса.
– координаты вектора относительно этого базиса.
Пусть заданы два базиса: 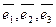 – «старый» и
– «старый» и 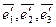 – «новый». Разложим вектор
– «новый». Разложим вектор 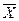 по этим базисам:
по этим базисам:
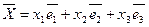 ,
,
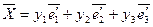 .
.
Найдем связь «старых» и «новых» координат вектора 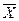 . Для этого запишем:
. Для этого запишем:
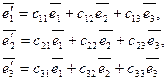
и подставим в 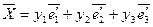 :
:
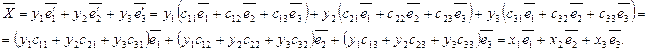 Из равенства векторов получим:
Из равенства векторов получим:
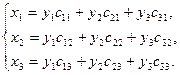
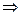
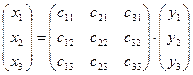 .
.
Отсюда замечаем, что матрица, по столбцам которой стоят координаты базисных векторов 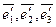 , является матрицей перехода от «старого» базиса к «новому» базису.
, является матрицей перехода от «старого» базиса к «новому» базису.
Обозначим ее через 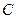 и получим замену «старых» координат «новыми»:
и получим замену «старых» координат «новыми»:
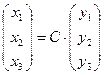 , где
, где 
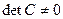 . Обратно, замена «новых» на «старые» координаты будет осуществляться с помощью обратной матрицы:
. Обратно, замена «новых» на «старые» координаты будет осуществляться с помощью обратной матрицы: 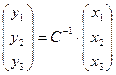 .
.
Линейные операторы
Если указано правило, по которому вектору 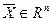 ставится в соответствие единственный вектор
ставится в соответствие единственный вектор 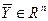 , то говорят, что задан оператор
, то говорят, что задан оператор 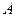 , такой, что
, такой, что
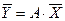 . .
|
Он обладает свойствами:
1. 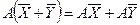 – аддитивность;
– аддитивность;
2. 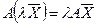 – однородность,
– однородность,
и называется линейным оператором.
При этом вектор 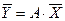 называют образом вектора
называют образом вектора 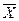 , а сам вектор
, а сам вектор 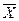 – прообразом вектора
– прообразом вектора 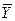 . Мы рассматриваем только случай, когда оператор
. Мы рассматриваем только случай, когда оператор 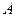 задается матрицей
задается матрицей 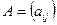 , где
, где 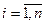 ,
, 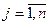 , поэтому для него справедливы свойства:
, поэтому для него справедливы свойства:
3. 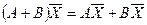 ;
;
4. 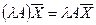 ;
;
5. 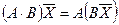 ;
;
6. существует нулевой оператор 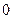 , такой, что
, такой, что 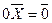 ;
;
7. существует тождественный оператор 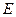 , такой, что
, такой, что 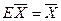 .
.
Если 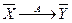 и
и 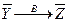 , то
, то 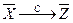 , где
, где 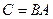 . Действительно,
. Действительно, 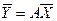 и
и 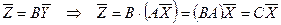 . Это есть свойство транзитивности линейного оператора.
. Это есть свойство транзитивности линейного оператора.
Теорема 3. Матрицы 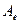 и
и 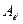 линейного оператора в базисах
линейного оператора в базисах 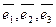 и
и 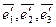 связаны соотношением
связаны соотношением
| (19) |
где 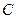 – матрица перехода от «старого» базиса
– матрица перехода от «старого» базиса 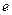 к «новому» базису
к «новому» базису 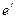 .
.
Доказать теорему самостоятельно.
Пример 13
В базисе 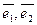 линейный оператор задан матрицей
линейный оператор задан матрицей 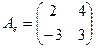 . Найти матрицу оператора в базисе
. Найти матрицу оператора в базисе 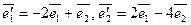 .
.
Решение
Составим матрицу 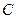 перехода от «старого» базиса
перехода от «старого» базиса 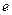 к «новому»
к «новому» 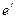 , по столбцам которой стоят координаты векторов
, по столбцам которой стоят координаты векторов 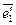 и
и 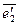 :
:
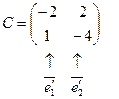 .
.
Тогда по формуле 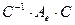 получим вид матрицы
получим вид матрицы 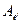 линейного оператора в «новом» базисе. Для этого построим обратную матрицу
линейного оператора в «новом» базисе. Для этого построим обратную матрицу 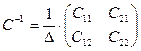 , где
, где 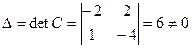 . Алгебраические дополнения:
. Алгебраические дополнения: 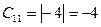 ,
, 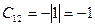 ,
, 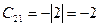 ,
, 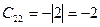 , отсюда
, отсюда 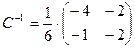 . Находим
. Находим 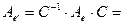
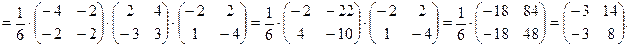
Ответ: матрица линейного оператора в «новом» базисе имеет вид 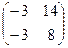 .
.
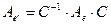 ,
,