Вектор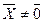 
называется собственным вектором линейного оператора 
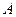, если действие этого оператора на 
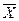сводится к растяжению вектора в 
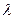раз, т.е.
 .
|
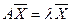Число 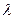при этом называют собственным значением оператора .
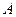Из данного определения следует схема получения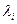 
и 
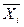. Перепишем 
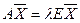или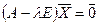 
и так как 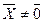, то
 .
|
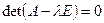В развернутом виде получим однородную систему:
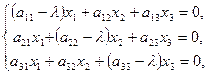
| (20) |
которая называется характеристической, и будет иметь ненулевое решение, если ее определитель обращается в нуль:
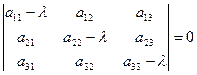
| (21) |
Уравнение (21) называется характеристическим (или вековым) и служит для получения собственных значений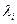 
. После раскрытия определителя приходим к алгебраическому уравнению 3-й степени вида:
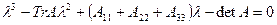
| (22) |
где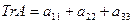 
– след матрицы 
; 
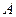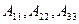– алгебраические дополнения, 
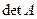– определитель матрицы .
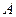Пусть уравнение (22) имеет три действительных корня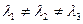 
. Тогда из системы (20) находим координаты собственных векторов 
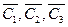. Составим матрицу 
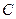, по столбцам которой стоят координаты этих векторов. Это матрица перехода от стандартного базиса 
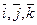к базису из собственных векторов и тогда линейный оператор 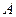в этом базисе будет иметь матрицу вида:
 ,
|
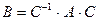причем диагональную, по главной диагонали которой стоят собственные значения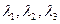 
, т.е.
.
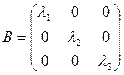Это справедливо только для случая различных действительных корней.
Предлагаем студентам проверить это самостоятельно.
Замечание. Если матрица линейного оператора симметрическая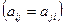 
, то ее собственные значения действительные и различные, а собственные векторы ортогональны.
Предлагаем студентам проверить это самостоятельно.
Пример 14
Найти собственные векторы и собственные значения линейного оператора, заданного в некотором базисе симметрической матрицей
|
|
.
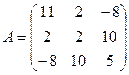Решение
Искомый собственный вектор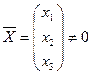 
удовлетворяет характеристической системе
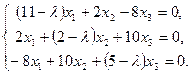
Собственные значения 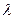удовлетворяют уравнению 
.
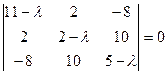После раскрытия определителя получаем алгебраическое уравнение 3-й степени: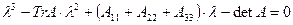 
, где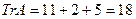 
,
, 
, 
,
.
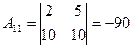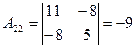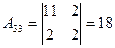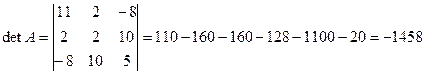Приходим к уравнению вида:
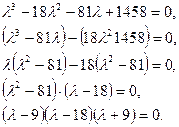
Получаем собственные значения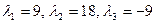 
– все действительные и различные.
Строим собственные векторы. Значение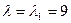 
подставляем в характеристическую систему:
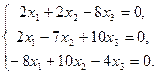
Ее определитель равен нулю, и, следовательно, ранг системы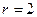 
(т.к. минор 
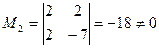). Система равносильна системе:
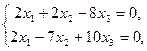или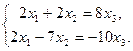 
, 
, 
.
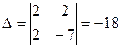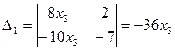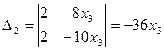По правилу Крамера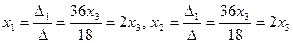 
. Полагаем 
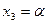и получаем 1-й собственный вектор 
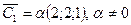. Можно взять 
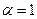и тогда 
.
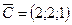Аналогично значение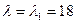 
подставляем в характеристическую систему:
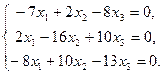
Вновь система равносильна двум уравнениям:
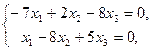т. к. минор 
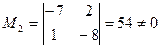и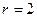 
. Находим решения системы 
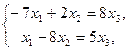по формулам Крамера:
; 
; 
.
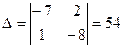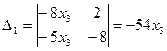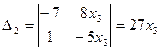Получаем координаты второго собственного вектора: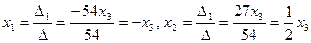 
. Полагаем 
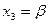и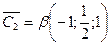 
, 
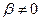. Можно взять 
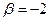и тогда 
.
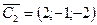Далее берем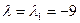 
и подставляем в характеристическую систему:
, 
, 
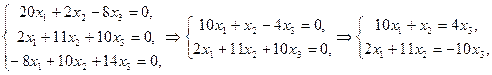
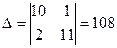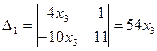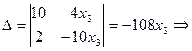
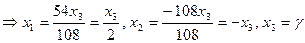. Получим 3-й собственный вектор 
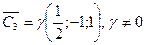. Можно взять 
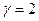, тогда 
.
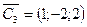Ответ: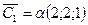 
, 
, 
, 
.
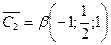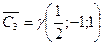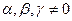Заметим, что построенные векторы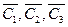 
взаимно перпендикулярны в пространстве, т. к. 
, 
, 
.
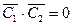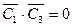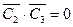Собственные векторы можно нормировать:
, 
, 
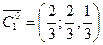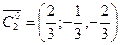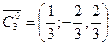– эти три вектора образуют ортонормированный базис в 3-х мерном пространстве.
Показать, что матрица линейного оператора в базисе из собственных векторов будет иметь диагональную форму: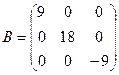 
.