I. ВВЕДЕНИЕ В ЛИНЕЙНУЮ АЛГЕБРУ. КРАТКИЙ ОБЗОР
A. Матрицы. Начальные сведения
Рассматриваем новый математический объект – матрицу. Это абстрактная таблица, состоящая из 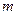 строк и
строк и 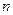 столбцов вида:
столбцов вида:
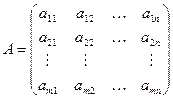 , ,
| (1) |
где 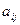 – элементы матрицы, стоящие на пересечении
– элементы матрицы, стоящие на пересечении 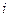 -ой строки и
-ой строки и 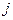 -го столбца. Элементы
-го столбца. Элементы 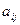 могут быть любой природы (числа, многочлены, функции и др.) При этом говорят, что матрица
могут быть любой природы (числа, многочлены, функции и др.) При этом говорят, что матрица 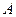 имеет размерность
имеет размерность 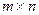 , и кратко записывают
, и кратко записывают 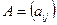 , где
, где 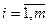 ,
, 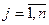 .
.
Если число строк равно числу столбцов, то матрица называется квадратной. Например, 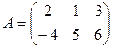 – прямоугольная, а
– прямоугольная, а 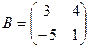 – квадратная матрица.
– квадратная матрица.
Элементы 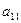 ,
, 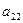 ,
, 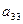 ,…,
,…, 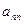 образуют главную диагональ в матрице
образуют главную диагональ в матрице 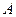 . Если ниже главной диагонали стоят нулевые элементы, то матрица называется треугольной, например
. Если ниже главной диагонали стоят нулевые элементы, то матрица называется треугольной, например
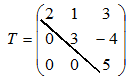
| ||
| Матрица вида | 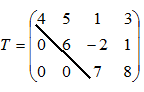
| называется трапециевидной. |
Если вне главной диагонали стоят нулевые элементы, то матрица называется диагональной, например
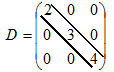
| ||
| Матрица вида | 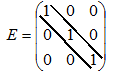
| является единичной. |
Матрица, состоящая только из нулевых элементов, называется нулевой матрицей: 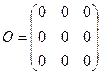
Если элементы матрицы, стоящие на симметричных местах относительно главной диагонали совпадают: 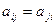 , то такая матрица называется симметрической.
, то такая матрица называется симметрической.
| Например | 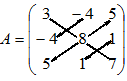
|
Матрица вида  называется матрицей-строкой, а матрица вида называется
называется матрицей-строкой, а матрица вида называется 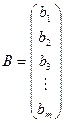 – матрицей-столбцом.
– матрицей-столбцом.
B. Операции над матрицами
Сложение матриц и умножение матрицы на число называются линейными операциями. Они выполняются по следующим правилам:
1) 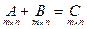 , где
, где 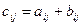 .
.
2) 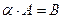 , где
, где 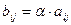 .
.
Пример 1
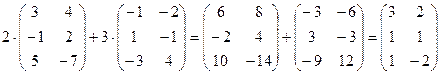 .
.
2. Умножение матриц выполняется по следующей схеме:
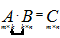 , где
, где 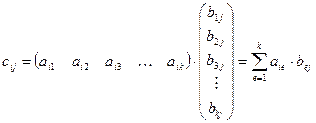 .
.
Заметим, что в левой матрице число столбцов совпадает с числом строк в правой матрице. Только в этом случае операция умножения возможна.
Пример 2
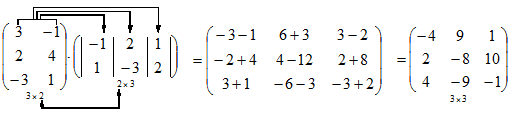
Пример 3
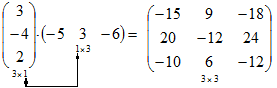
Замечание. В общем случае умножение матриц неперестановочно, т.е. 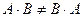 . Однако, можно подобрать две квадратные матрицы, чтобы
. Однако, можно подобрать две квадратные матрицы, чтобы 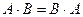 , в этом случае говорят, что матрицы коммутируют.
, в этом случае говорят, что матрицы коммутируют.
Пример 4
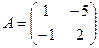 ,
, 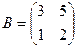 ,
,
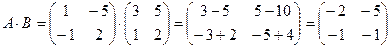 ;
;
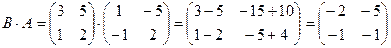 .
.
Матрицы можно возводить в степень, причем только квадратные, т.е. число столбцов должно соответствовать числу строк.
Рассмотрим еще одну операцию над матрицами – транспонирование. При транспонировании матрицы 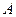 ее строки и столбцы меняются местами с сохранением порядка. Обозначается
ее строки и столбцы меняются местами с сохранением порядка. Обозначается 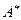 или
или 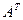 . Транспонировать можно матрицы любой размерности.
. Транспонировать можно матрицы любой размерности.
Пример 5
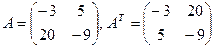 .
.
C. Определители квадратных матриц
Прежде чем ввести операцию обращения матриц 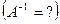 , необходимо дать понятие определителя квадратной матрицы. Для квадратной матрицы размера 2×2 определителем является число Δ, получающееся по формуле
, необходимо дать понятие определителя квадратной матрицы. Для квадратной матрицы размера 2×2 определителем является число Δ, получающееся по формуле
| (2) |
Таким образом, 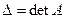 , где
, где  – первые три буквы от латинского determinantis (определитель). Так легко получается детерминант 2-го порядка.
– первые три буквы от латинского determinantis (определитель). Так легко получается детерминант 2-го порядка.
Пример 6
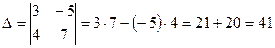 .
.
Однако для матрицы размера 3×3 определитель строится сложнее:
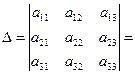
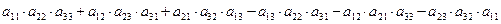
| (3) |
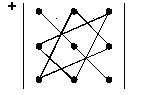
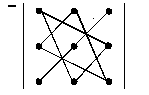
Для простоты запоминания пользуются следующими схемами:
| первые три суммы | последние три суммы |
| 
|
Схема называется правилом треугольников.
Модифицируем его, т.е. распрямим треугольники.
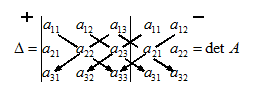
| – схема Саррюса. | (4) |
Если квадратная матрица имеет размер 4×4 и выше, то для вычисления ее определителя применяется правило Лапласа:
| (5) |
т.е. детерминант матрицы 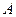 равен сумме произведений элементов
равен сумме произведений элементов 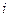 -ой строки (или
-ой строки (или 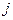 -го столбца) на соответствующие алгебраические дополнения.
-го столбца) на соответствующие алгебраические дополнения.
При этом 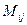 – минор (определитель
– минор (определитель 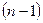 -го порядка), получающийся из матрицы
-го порядка), получающийся из матрицы 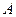 вычеркиванием
вычеркиванием 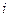 -ой строки и
-ой строки и 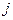 -го столбца,
-го столбца, 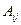 – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу 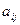 .
.
Заметим, что правило Лапласа позволяет определители 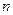 -го порядка вычислять через определители
-го порядка вычислять через определители 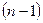 -го порядка.
-го порядка.
Пример 7
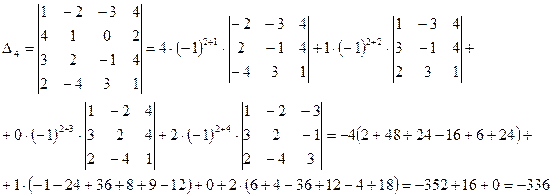
Замечание. Если определитель матрицы приведен к треугольному виду
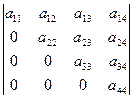 ,
,
то его значение равно произведению элементов, стоящих по главной диагонали, т.е. 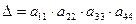 . Это автоматически следует из правила Лапласа.
. Это автоматически следует из правила Лапласа.
Отметим элементарные преобразования (Э.П.) над строками определителя, которые не меняют его значения:
2.3. вынесение общего множителя строки за знак определителя;
2.4. прибавление к одной строке элементов другой строки;
2.5. прибавление к одной строке элементов другой, умноженных на некоторое число.
Пример 8
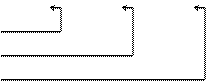
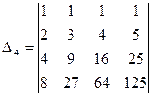




 + =
+ =

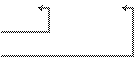
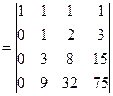
 +
+ 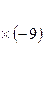

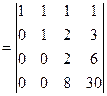
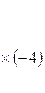

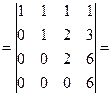
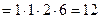
Замечание 1. Такие же Э.П. можно выполнять и над столбцами определителя.
Замечание 2. Определитель 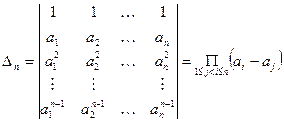
и называется определителем Вандермонда.
Студентам предлагается доказать это самостоятельно.
d. Нахождение обратной матрицы
Теперь можно перейти к обращению квадратных матриц. В этом случае 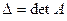 должен быть отличным от нуля, и матрица
должен быть отличным от нуля, и матрица 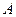 является невырожденной. Для такой матрицы существует обратная матрица
является невырожденной. Для такой матрицы существует обратная матрица 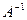 , причем
, причем 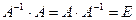 дает единичную матрицу. Легко показать, что обратная матрица имеет вид:
дает единичную матрицу. Легко показать, что обратная матрица имеет вид:
| (6) |
где 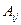 – алгебраические дополнения элементов
– алгебраические дополнения элементов  исходной матрицы:
исходной матрицы:
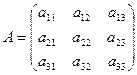
поскольку
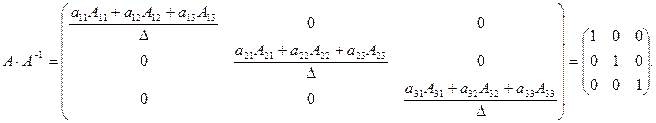 Предлагаем студентам самостоятельно это проверить.
Предлагаем студентам самостоятельно это проверить.
Замечание. Обратную матрицу можно построить с помощью элементарных преобразований по следующей схеме:
| (7) |
Пример 9
С помощью элементарных преобразований провести обращение матрицы
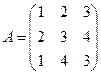 .
.
Решение


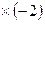 + – ~
+ – ~ 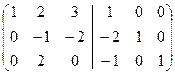
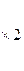 + ~
+ ~
 ~
~ 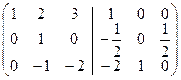 + ~
+ ~ 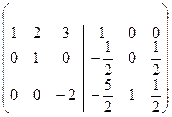
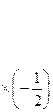 ~
~

 ~
~ 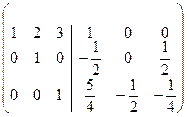
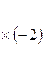 + ~
+ ~ 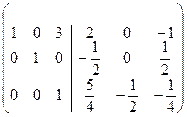
 + ~
+ ~
~ 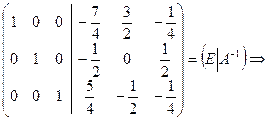
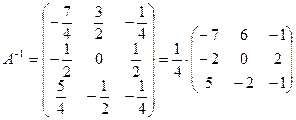 .
.
Действительно,
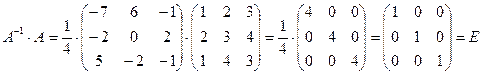 .
.
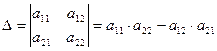
 где:
где: 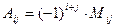 ,
,
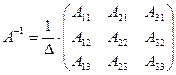 ,
,
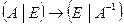 .
.