Механизм, состоящий из нескольких звеньев, совершает движение в плоскости чертежа. Ведущее звено механизма – кривошип OA – вращается вокруг неподвижной оси с постоянной угловой скоростью  и приводит в движение ведомые звенья AB, O 1 B, EF и т.д.
и приводит в движение ведомые звенья AB, O 1 B, EF и т.д.
1. На чертеже изобразить в соответствующем масштабе механизм в заданном положении ведущего звена (масштаб указать).
2. Выяснить вид движения каждого звена (поступательное, вращательное, плоскопараллельное).
В механизмах, рассматриваемых в различных вариантах зада-ния, встречаются ползуны, перемещающиеся вдоль своих направ-ляющих, т.е. совершающие поступательное движение. Кроме того, присутствуют кривошипы (на чертежах это стержни, имеющие неподвижную точку). Они совершают вращение вокруг неподвиж-ной оси, проходящей через неподвижную точку, перпендикулярно плоскости чертежа. И, наконец, остальные стержни (не имеющие неподвижной точки) перемещаются в плоскости чертежа, т.е. совершают плоскопараллельное движение.
3. Выбрать систему отсчета, с которой связать оси координат Oxyz так, чтобы ось  была направлена перпендикулярно плоскости чертежа на читателя.
была направлена перпендикулярно плоскости чертежа на читателя.
4. Определить скорость 
 точки A ведущего звена и изобразить этот вектор на чертеже в масштабе (масштаб указать). Вектор
точки A ведущего звена и изобразить этот вектор на чертеже в масштабе (масштаб указать). Вектор  направлен перпендикулярно отрезку OA в сторону вращения кривошипа.
направлен перпендикулярно отрезку OA в сторону вращения кривошипа.
5. Перейти к следующему звену - AB или ABF, совершающему плоскопараллельное движение, и найти для него положение мгновенного центра скоростей. Нам известны скорость точки A и линия действия скорости точки B (или точки F). Проведем перпендикуляры к скоростям. В точке пересечения перпендикуляров будет находиться мгновенный центр скоростей CAB звена AB (или ABF). Разделив  на расстояние ACAB, найдем угловую скорость
на расстояние ACAB, найдем угловую скорость  (или
(или  ) звена AB (или ABF). Направление вращения звена AB (или ABF) вокруг оси
) звена AB (или ABF). Направление вращения звена AB (или ABF) вокруг оси  найдем, зная направление скорости
найдем, зная направление скорости  . Зная
. Зная 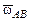 (или
(или  ) и положение точки CAB, определим скорости всех точек рассматриваемого звена. Для этого, соединив точки B, M, … с точкой CAB, измерим расстояния BCAB, MCAB, …. Умножив
) и положение точки CAB, определим скорости всех точек рассматриваемого звена. Для этого, соединив точки B, M, … с точкой CAB, измерим расстояния BCAB, MCAB, …. Умножив  (или
(или  ) на соответствующие расстояния, получим скорости
) на соответствующие расстояния, получим скорости  ,… Отложить скорости точек следует перпендикулярно отрезкам, соединяющим точки с мгновенным центром скоростей CAB, в направлении, определяемом поворотом рассматриваемого звена вокруг оси, проходящей через мгновенный центр скоростей.
,… Отложить скорости точек следует перпендикулярно отрезкам, соединяющим точки с мгновенным центром скоростей CAB, в направлении, определяемом поворотом рассматриваемого звена вокруг оси, проходящей через мгновенный центр скоростей.
6. Перейти к следующему звену. Если следующее звено, например O1B, совершает вращательное движение вокруг оси  , нужно определить его угловую скорость, разделив
, нужно определить его угловую скорость, разделив  на расстояние O 1 B от точки B до оси вращения. Направление вращения, т.е. направление
на расстояние O 1 B от точки B до оси вращения. Направление вращения, т.е. направление  , определится исходя из направления
, определится исходя из направления  .
.
7. Аналогично найти мгновенный центр скоростей второго звена, совершающего плоскопараллельное движение, и скорости отдельных его точек. При этом учесть, что скорости точек, принадлежащих звеньям, вращающимся вокруг неподвижных осей, направлены перпендикулярно радиусам вращения, а скорости
ползунов направлены по прямым, по которым перемещаются ползуны.
Все найденные скорости точек и угловые скорости звеньев изобразить на чертеже. Затем перейти к определению ускорений указанных на чертеже точек и угловых ускорений звеньев.
Ускорение точки A ведущего звена OA, вращающегося вокруг неподвижной оси, определить по формуле  , где
, где  – вращательное ускорение точки A. Так как кривошип OA вращается с постоянной угловой скоростью
– вращательное ускорение точки A. Так как кривошип OA вращается с постоянной угловой скоростью 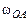 , то угловое ускорение
, то угловое ускорение  ,
,  и
и  , где
, где 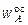 – осестремительное ускорение точки A.
– осестремительное ускорение точки A.
Звено OA приводит в движение ведомое звено (например, AB), совершающее плоскопараллельное движение. Найти ускоре-
ние точки B (или другой точки), которая либо является ползу-
ном, либо принадлежит звену O1B, вращающемуся вокруг неподвижной оси  . Ускорение искать по методу полюса, приняв за полюс точку A:
. Ускорение искать по методу полюса, приняв за полюс точку A:
 . (3.1)
. (3.1)
Ускорение полюса  строить в точке B. Определить
строить в точке B. Определить  – осестремительное ускорение точки B по отношению полюса A. Отложить
– осестремительное ускорение точки B по отношению полюса A. Отложить  в масштабе (масштаб указать), направляя его по звену от точки B к полюсу.
в масштабе (масштаб указать), направляя его по звену от точки B к полюсу.
Вращательное ускорение точки B по отношению к полюсу A:  определить нельзя, так как
определить нельзя, так как  неизвестно
неизвестно
и найти его дифференцированием  по времени нельзя
по времени нельзя
( известна только для данного положения механизма).
известна только для данного положения механизма).
Для  известна только его линия действия, перпендикулярная AB. По ней направить ось
известна только его линия действия, перпендикулярная AB. По ней направить ось  , считая, что вектор
, считая, что вектор  сонаправлен с
сонаправлен с  . Далее действовать в зависимости от того, чем является точка B. Если точка B – ползун, то направить ось
. Далее действовать в зависимости от того, чем является точка B. Если точка B – ползун, то направить ось  вдоль направляющей ползуна, ось
вдоль направляющей ползуна, ось  перпендикулярно
перпендикулярно  .
.
Проецируя (3.1) на оси  и
и  , найти
, найти  и
и  (углы снимаем с чертежа). Если они положительны, то направить векторы
(углы снимаем с чертежа). Если они положительны, то направить векторы  и
и  в сторону осей
в сторону осей  и
и  соответственно, если отрицательны, то в противоположную осям сторону.
соответственно, если отрицательны, то в противоположную осям сторону.
Величина углового ускорения  , а его направление определить из векторного равенства:
, а его направление определить из векторного равенства: 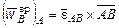 .
.
Если точка B принадлежит кривошипу, то записать ускорение точки B как точки O 1 B при вращательном движении:
 . (3.2)
. (3.2)
Осестремительное ускорение точки B по отношению к оси  найти по формуле
найти по формуле  и направить к оси вращения. Туда же направить ось
и направить к оси вращения. Туда же направить ось  .
.
Для вращательного ускорения 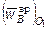 , зная линию действия (по линии действия
, зная линию действия (по линии действия  ), по ней направить ось
), по ней направить ось  .
.
Приравнять равенства (3.1) и (3.2):
 . (3.3)
. (3.3)
Спроецировать (3.3) на оси  и
и  и найти
и найти  и
и 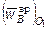 . По ним найти
. По ним найти  и
и  . Направления угловых ускорений определить из векторных равенств
. Направления угловых ускорений определить из векторных равенств  и
и  . По равенству (3.2) опреде-лить ускорение
. По равенству (3.2) опреде-лить ускорение  . Затем найти ускорение точек M, F, …, принадлежащих звену AB. Так как,
. Затем найти ускорение точек M, F, …, принадлежащих звену AB. Так как,  нам уже известно, то ускорение найти по методу полюса, геометрически складывая три составляющие.
нам уже известно, то ускорение найти по методу полюса, геометрически складывая три составляющие.
Затем перейти к ускорению точки, принадлежащей следую-щему звену, действуя при этом согласно изложенной выше схеме.
При определении касательного и нормального ускорения точки B следует учесть следующее. Если точка B – ползун, т.е. перемещается по прямой, то полное ускорение точки B равно касательному ускорению, а нормальное ускорение тождественно равно нулю. Если точка B принадлежит кривошипу, то осестремительное ускорение по отношению к оси  является нормальным ускорением точки B, а вращательное ускорение – касательным. Если точка B принадлежит звену, совершающему плоскопараллельное движение, то нужно разложить ее ускорение на две взаимно перпендикулярные составляющие, направив одну из них по скорости, – это касательное ускорение точки B, вторая составляющая - нормальное ускорение.
является нормальным ускорением точки B, а вращательное ускорение – касательным. Если точка B принадлежит звену, совершающему плоскопараллельное движение, то нужно разложить ее ускорение на две взаимно перпендикулярные составляющие, направив одну из них по скорости, – это касательное ускорение точки B, вторая составляющая - нормальное ускорение.
Если касательное ускорение точки B совпадает по направлению со скоростью, то движение точки B ускоренное, если противоположно скорости, то замедленное. Если скорость точки B в данном положении механизма равна нулю, то точка B совершает мгновенную остановку. Чертеж и все расчеты данной работы можно выполнить, используя графический редактор «Компас».
Исходные данные
| Вар. | OA | AB | O 1 B | O 1 E | EF | O 1 O | BE | AF | AM | a | b | c | α | φ | ω |
| м | град | град | рад∙с-1 | ||||||||||||
| 0,4 0,4 0,4 | 1,0 1,14 1,1 | 0,4 0,4 0,4 | - | 0,8 0,8 0,8 | 1,0 1,0 1,0 | - | - | 0,5 0,7 0,5 | - | - | - | 1,2 1,4 1,6 | |||
| 0,5 0,5 0,5 | 0,5 0,72 0,56 | 0,4 0,4 0,4 | - | 1,2 1,2 1,2 | - | - | - | 0,2 0,54 0,4 | 0,2 0,2 0,2 | 0,3 0,3 0,3 | 0,5 0,5 0,5 | 1,2 1,4 1,6 | |||
| 0,5 0,5 0,5 | 0,6 1,44 1,4 | 0,5 0,5 0,5 | - | - | - | 1,2 1,2 1,2 | - | 0,4 1,06 0,7 | 0,8 0,8 0,8 | 0,4 0,4 0,4 | - | - | 1,2 1,4 1,6 | ||
| 0,3 0,3 0,3 | 0,2 0,62 0,8 | - | - | - | - | 0,8 0,8 0,8 | 0,8 1,02 0,84 | 0,5 0,67 0,8 | - | - | - | 1,2 1,4 1,6 | |||
| 0,3 0,3 0,3 | 1,0 1,2 0,8 | 0,8 0,8 0,8 | - | 1,0 1,0 1,0 | 1,5 1,5 1,5 | 0,8 0,8 0,8 | - | 0,6 0,7 0,4 | 0,4 0,4 0,4 | - | - | 1,2 1,4 1,6 | |||
| 0,36 0,36 0,36 | 0,72 1,2 1,04 | - | - | 0,94 0,94 0,94 | - | - | 0,5 1,1 0,52 | 0,24 0,65 0,62 | 0,8 0,8 0,8 | - | - | 1,2 1,4 1,6 | |||
| 0,3 0,3 0,3 | 0,96 0,86 1,04 | 0,6 0,6 0,6 | - | 1,1 1,1 1,04 | - | - | 1,18 1,06 1,25 | 0,4 0,44 0,4 | 1,6 1,6 1,6 | 0,7 0,7 0,7 | - | - | 1,2 1,4 1,6 |
| Вар. | OA | AB | O 1 B | O 1 E | EF | O 1 O | BE | AF | AM | a | b | c | α | φ | ω |
| м | град | град | рад∙с-1 | ||||||||||||
| 0,4 0,4 0,4 | 1,0 1,32 0,65 | 0,6 0,6 0,6 | - | 1,0 0,9 0,95 | 0,8 0,8 0,8 | - | 0,8 1,14 0,46 | 0,2 1,0 0,24 | 0,3 0,3 0,3 | - | - | - | 1,2 1,4 1,6 | ||
| 0,6 0,6 0,6 | 1,12 1,28 1,06 | - | 0,7 0,7 0,7 | 0,7 0,7 0,7 | - | 0,6 0,6 0,6 | - | 0,5 0,5 0,5 | 2,0 2,0 2,0 | 0,5 0,5 0,5 | - | 1,2 1,4 1,6 | |||
| 0,3 0,3 0,3 | 0,6 0,64 0,42 | 0,7 0,7 0,8 | - | 0,2 0,2 0,2 | 1.0 1,0 1,0 | - | 0,7 0,77 0,54 | 0,2 0,2 0,2 | 0,8 0,8 0,8 | 0,4 0,4 0,4 | - | - | 1,2 1,4 1,6 | ||
| 0,27 0,27 0,27 | 0,6 0,5 0,76 | 0,6 0,6 0,6 | - | 0,6 0,54 0,62 | 1,0 1,0 1,0 | - | 0,5 0,5 0,57 | 0,3 0,3 0,41 | - | - | - | - | 1,2 1,4 1,6 | ||
| 0,4 0,4 0,4 | 0,5 0,55 1,15 | 0,6 0,6 0,6 | 0,6 0,6 0,6 | 1,2 1,2 1,2 | 0,8 0,8 0,8 | - | - | 0,25 0,25 0,25 | - | - | - | 1,2 1,4 1,6 | |||
| 0,4 0,4 0,4 | 0,4 0,3 0,37 | 0,5 0,5 0,5 | 0,3 0,3 0,3 | 0,7 0,7 0,7 | 0,6 0,6 0,6 | - | - | 0,2 0,12 0,15 | - | - | - | 1,2 1,4 1,6 | |||
| 0,3 0,3 0,3 | 0,5 0,42 0,52 | 0,7 0,7 0,7 | - | 0,6 0,6 0,6 | 0,9 0,9 0,9 | - | 0,2 0,13 0,22 | 0,3 0,3 0,3 | - | - | - | - | 1,2 1,4 1,6 |
| Вар. | OA | AB | O 1 B | O 1 E | EF | O 1 O | BE | AF | AM | a | b | c | α | φ | ω |
| м | град | град | рад∙с-1 | ||||||||||||
| 0,3 0,3 0,3 | 0,8 0,55 0,47 | 0,5 0,5 0,5 | - | 1,0 1,0 0,9 | 0,7 0,7 0,7 | 0,3 0,3 0,3 | - | 0,4 0,16 0,3 | - | - | - | - | 1,2 1,4 1,6 | ||
| 0,3 0,3 0,3 | 0,58 0,5 0,62 | - | - | - | - | 0,7 0,7 0,7 | 0,2 0,2 0,2 | 0,3 0,3 0,3 | 1,0 1,0 1,0 | 0,7 0,7 0,7 | - | 1,2 1,4 1,6 | |||
| 0,25 0,25 0,25 | 0,65 0,9 0,82 | - | - | 0,8 0,9 0,9 | - | - | 0,45 0,45 0,45 | 0,25 0,28 0,25 | 0,4 0,4 0,4 | - | - | - | 1,2 1,4 1,6 | ||
| 0,45 0,45 0,45 | 0,87 0,61 1,42 | 0,7 0,7 0,7 | 0,4 0,4 0,4 | 0,62 0,62 0,62 | 0,5 0,5 0,5 | - | - | 0,62 0,42 1,15 | - | - | - | 1,2 1,4 1,6 | |||
| 0,3 0,3 0,3 | 0,7 0,93 0,8 | 0,5 0,5 0,5 | 0,7 0,7 0,7 | 0,7 0,7 0,7 | - | - | - | 0,5 0,73 0,6 | 0,4 0,4 0,4 | 0,3 0,3 0,3 | 0,3 0,3 0,3 | - | 1,2 1,4 1,6 | ||
| 0,3 0,3 0,3 | 0,9 0,62 0,75 | 0,3 0,3 0,3 | - | 0,4 0,58 0,38 | 0,8 0,8 0,8 | - | 0,3 0,19 0,14 | 0,7 0,39 0,5 | 0,2 0,2 0,2 | - | - | - | 1,2 1,4 1,6 | ||
| 0,4 0,4 0,4 | 1.0 0,56 1,25 | 0,6 0,6 0,6 | 0,2 0,2 0,2 | 0,6 0,6 0,6 | 0,8 0,8 0,8 | - | - | 0,3 0,38 0,6 | - | 0,2 0,2 0,2 | - | - | 1,2 1,4 1,6 |
| Вар | OA | AB | O1B | O1E | EF | O1O | BE | AF | AM | a | b | c | α | φ | ω |
| м | град | град | рад∙с-1 | ||||||||||||
| 0,3 0,3 0,3 | 0,6 0,32 0,14 | 0,5 0,5 0,5 | - | 0,8 0,8 0,96 | 0,36 0,36 0,36 | - | 0,4 0,13 0,08 | 0,2 0,25 0,1 | - | 0,9 0,9 0,9 | - | - | 1,2 1,4 1,6 | ||
| 0,4 0,4 0,4 | 1,2 0,46 1,2 | 0,2 0,2 0,2 | - | 0,9 0,9 0,9 | 1,0 1,0 1,0 | - | 1,0 0,26 1,0 | 0,3 0,13 0,73 | - | 0,5 0,5 0,5 | - | - | 1,2 1,4 1,6 | ||
| 0,5 0,5 0,5 | 1,0 1,9 0,53 | - | - | 0,6 0,6 0,32 | - | - | 0,3 1,2 0,83 | 0,1 1,0 0,5 | - | 0,4 0,4 0,5 | - | - | 1,2 1,4 1,6 | ||
| 0,4 0,4 0,4 | 1,2 0,62 1,0 | 0,2 0,2 0,2 | - | 0,5 0,5 0,5 | 1,0 1,0 1,0 | - | 0,7 0,25 0,53 | 0,4 0,5 0,76 | - | 0,3 0,3 0,3 | - | - | 1,2 1,4 1,6 |
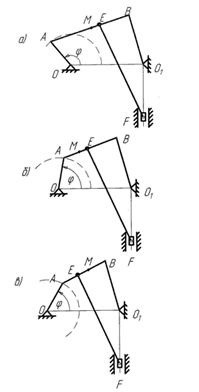
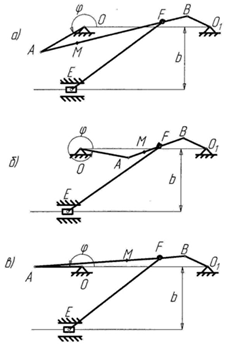
П р и м е ч а н и е. Рисунок (а) соответствует первой строке данных; рисунок (б) – второй; рисунок (в) – третьей.
Вариант 1Вариант 2


Вариант 3Вариант 4


Вариант 5Вариант 6

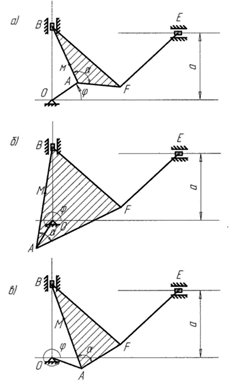
Вариант 7Вариант 8


Вариант 9Вариант 10


Вариант 11Вариант 12
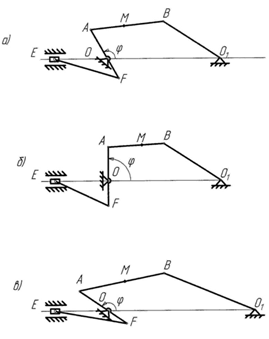

Вариант 13Вариант 14


Вариант 15Вариант 16

Вариант 17Вариант18


Вариант 19Вариант 20


Вариант 21Вариант 22


Вариант 23Вариант 24

Вариант 25

П р и м е р (см. рис. 3.1). Звено ОА и треугольник О 1 BF вра-щаются вокруг неподвижных осей  и
и  , перпендикулярных плоскости чертежа, ползун E перемещается вдоль вертикальной направляющей, совершая поступательное движение, звенья AB и FE совершают плоскопараллельное движение. Скорость точки A
, перпендикулярных плоскости чертежа, ползун E перемещается вдоль вертикальной направляющей, совершая поступательное движение, звенья AB и FE совершают плоскопараллельное движение. Скорость точки A  м/с,
м/с,  перпендикулярна отрезку OA и направлена в сторону вращения кривошипа. Найдем мгновенный центр скоростей звена AB. Перпендикуляром к скорости
перпендикулярна отрезку OA и направлена в сторону вращения кривошипа. Найдем мгновенный центр скоростей звена AB. Перпендикуляром к скорости  является звено O 1 B. Так как OA||O 1 B, то
является звено O 1 B. Так как OA||O 1 B, то  ||
||  и при этом
и при этом  не перпендикулярна отрезку AB, соединяющему точки, т.е. в данный момент времени звено AB совершает мгновенное поступательное движение,
не перпендикулярна отрезку AB, соединяющему точки, т.е. в данный момент времени звено AB совершает мгновенное поступательное движение,  и скорости точек B и M геометрически равны скорости
и скорости точек B и M геометрически равны скорости  . Откладываем их на чертеже. Найдем угловую скорость треугольника:
. Откладываем их на чертеже. Найдем угловую скорость треугольника:  рад /с.
рад /с.
 |
Рис. 3.1
По направлению  определим, что звено BO 1 F вращается по часовой стрелке. Так как O 1 F=O 1 B, то
определим, что звено BO 1 F вращается по часовой стрелке. Так как O 1 F=O 1 B, то  . Откладываем
. Откладываем  перпендикулярно отрезку O 1 F, соединяющему точку F с осью вращения
перпендикулярно отрезку O 1 F, соединяющему точку F с осью вращения  . Ищем точку СFE - мгновенный центр скоростей звена FE. Для этого продолжаем отрезок O 1 F и проводим горизонтальную прямую через точку Е (перпендикуляр к
. Ищем точку СFE - мгновенный центр скоростей звена FE. Для этого продолжаем отрезок O 1 F и проводим горизонтальную прямую через точку Е (перпендикуляр к  , которая направлена вдоль вертикальной образующей ползуна). Найдем угловую скорость звена FE:
, которая направлена вдоль вертикальной образующей ползуна). Найдем угловую скорость звена FE:  рад /с.
рад /с.
По направлению  определим, что звено FE поворачивается вокруг оси
определим, что звено FE поворачивается вокруг оси  по часовой стрелке. Скорость ползуна E найдем по формуле
по часовой стрелке. Скорость ползуна E найдем по формуле  м/с,
м/с,  направлена по вертикали вниз.
направлена по вертикали вниз.
Ускорение точки A ведущего звена OA определим по формуле  .
.
Вращательное ускорение 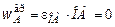 , так как звено OA вращается с постоянной угловой скоростью, т.е.
, так как звено OA вращается с постоянной угловой скоростью, т.е.  м/с2,
м/с2,  откладываем в масштабе и направляем от точки A к оси вращения
откладываем в масштабе и направляем от точки A к оси вращения  . Ищем ускорение точки B по методу полюса, приняв за полюс точку A:
. Ищем ускорение точки B по методу полюса, приняв за полюс точку A:
 , (3.4)
, (3.4)
 параллельным переносом строим в точке B:
параллельным переносом строим в точке B:  , так как
, так как  ;
;  , но ε AB нам не известно. Перпендикулярно AB проводим ось
, но ε AB нам не известно. Перпендикулярно AB проводим ось  и считаем, что
и считаем, что  сонаправлено с
сонаправлено с  . C другой стороны, ускорение точки B как точки кривошипа O 1 B равно:
. C другой стороны, ускорение точки B как точки кривошипа O 1 B равно:
 , (3.5)
, (3.5)
 м/с2,
м/с2,  отложим по О 1 B, направляя его из точки B к оси вращения
отложим по О 1 B, направляя его из точки B к оси вращения  . Туда же направим ось
. Туда же направим ось  .
.  , но
, но  нам также не известно. Будем считать, что
нам также не известно. Будем считать, что 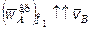 и направим по нему ось
и направим по нему ось  . Приравняем правые части (3.4) и (3.5):
. Приравняем правые части (3.4) и (3.5):
 . (3.6)
. (3.6)
Спроецируем (3.6) на оси  :
:
 ,
,
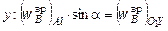 .
.
Из этих равенств находим:
 -0,984 м/с2,
-0,984 м/с2,  = -0,671 м/с2.
= -0,671 м/с2.
Направляем  и
и  .
.
Из формулы (3.5) находим ускорение точки B по теореме Пифагора:
 =0,743 м/с2.
=0,743 м/с2.
По формуле (3.4) проверяем правильность нахождения  . Находим угловые ускорения звеньев:
. Находим угловые ускорения звеньев:
 =0,728 рад/с2,
=0,728 рад/с2,  =1,342 рад/с2.
=1,342 рад/с2.
Направления векторов  и
и  определяем по правилу векторного произведения:
определяем по правилу векторного произведения:
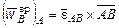 ,
,  направлен на читателя
направлен на читателя
 ,
,  направлен на читателя.
направлен на читателя.
Затем определяем ускорение точки F:
 ,
,
 ,
,  ,
,  , так как O 1 F=O 1 B.
, так как O 1 F=O 1 B.
Строим вектор  на чертеже.
на чертеже.
Теперь ищем ускорение точки M, приняв за полюс точку A:  ,
,  параллельным переносом строим в точке M,
параллельным переносом строим в точке M, 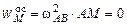 ,
,  м/с2.
м/с2.
Направление вектора  определяем из векторного произведения:
определяем из векторного произведения:  .
.  находим по теореме косинусов:
находим по теореме косинусов:
 =0,34 м/с2.
=0,34 м/с2.
Затем находим ускорение точки E, приняв за полюс точку F:
 . (3.7)
. (3.7)
 параллельным переносом строим в точке E:
параллельным переносом строим в точке E: 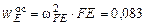 м/с2,
м/с2,  направляем по звену к точке F;
направляем по звену к точке F;  , но
, но  нам не известно. Перпендикулярно FE проводим ось
нам не известно. Перпендикулярно FE проводим ось 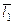 и считаем, что
и считаем, что  сонаправлено с
сонаправлено с 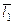 .
.
По направляющей ползуна направляем ось  , к точке СFE направляем ось
, к точке СFE направляем ось  .
.
Спроецируем равенство (3.7) на оси  ,
,  :
:
 ,
,
 .
.
Из этих равенств находим
 = -0,27 м/с2,
= -0,27 м/с2,  = 0,53 м/с2.
= 0,53 м/с2.
Угловое ускорение  определяем по формуле
определяем по формуле  =0,25 рад/с2, направление вектора
=0,25 рад/с2, направление вектора  - из векторного произведения:
- из векторного произведения:  , угловое ускорение
, угловое ускорение  направ-лено на читателя.
направ-лено на читателя.
З А Д А н и е К4