Движение точки задано кинематическими уравнениями в соответствии с номером варианта задачи (см. таблицу «Исходные данные» с. 10-14).
1. Определить траекторию точки и изобразить ее на чертеже. Указать на ней положение точки в заданные моменты времени, обозначив их М 0 и М 1 (М 0 – в момент времени t = 0; М 1 - в момент t = t 1).
2. Определить алгебраические величины проекций скорости точки в общем виде, а затем для момента времена t = t 1. По найденным алгебраическим величинам проекций скорости построить вектор на чертеже и вычислить его величину.
3. Определить алгебраические величины проекций ускорений точки на оси координат в общем виде, а затем для момента времени t = t 1. Построить вектор ускорения на чертеже и вычислить его величину.
4. Для определения касательного ускорения необходимо иметь проекцию вектора скорости точки на касательную в виде функции времени: 
, тогда касательное ускорение точки опреде-ляется по формуле 
. Определить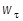 
для момента време-ни t = t 1 и построить этот вектор на чертеже.
5. Установить характер движения точки в момент времени t = t 1 (по направлениям векторов 
и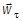 
). Если векторы сонаправлены, то движение точки ускоренное, если они противоположны по направлению, то – замедленное.
6. Нормальное ускорение точки в момент времени определяется из равенства
,
в котором каждый из векторов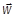 
и 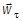вычислен в этот момент времени. Вектор 
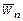построить на чертеже.
7. Радиус кривизны траектории точки в момент времени t = t 1 определить по формуле (1.4).
Исходные данные
| № вар. | x = x (t) | y = y (t) | z = z (t) | t 1, с |
| м | ||||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| |||
| 
| 
| ||
| 
| 
|
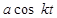
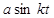
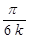
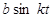
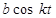
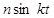
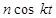
| № вар. | x = x (t) | y = y (t) | z = z (t) | t 1, с |
| м | ||||
| 
| |||
| 
| 
| ||
|
| 
| 
| ||
| 
| 
| ||
| 
| |||
| 
| 
| ||
| 
| |||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| |||
| 
|
| ||
| 
| |||
| 
| 
|
|
|
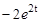
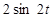
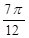
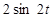
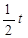
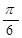
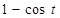
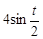
| № вар. | x = x (t) | y = y (t) | z = z (t) | t 1, с |
| м | ||||
| 
| 
| ||
| 
| |||
| 
| 
| ||
| 
| 
| ||
|
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
|
| ||
| 
| 
| ||
|
| |||
| 
| |||
| 
| 
|
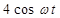
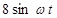
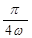
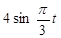
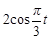
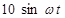
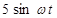
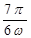
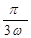
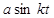
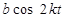
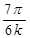
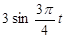
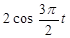
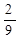
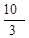
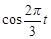
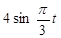
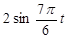
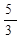
| № вар. | x = x (t) | y = y (t) | z = z (t) | t 1, с |
| м | ||||
| 
| 
| ||
| 
| |||
|
|
| ||
|
| 
| ||
|
|
| 
| ||
| 
| 
| ||
| 
| |||
|
| 
| |||
| 
| 
| ||
|
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| |||
| 
|
| ||
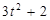
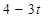
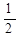
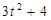
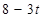
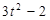
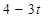
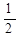
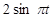
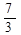
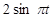
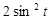
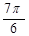
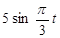
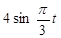
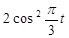
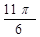
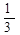
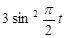
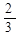
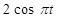
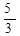
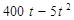
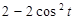
| t | 
| |||
| 
| 
| ||
| 
|
| ||
| 
|
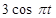
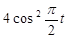
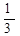
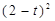
| № вар. | x = x (t) | y = y (t) | z = z (t) | t 1, с |
| м | ||||
| 
| 
| ||
|
|
|
| ||
| 
| 
| ||
| 
|
| ||
| 
| |||
|
| 
|
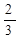
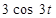
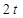
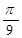
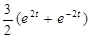
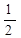
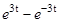
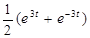
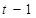
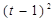
П р и м е р. Движение точки задано кинематическими урав-нениями: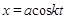 
; 
; 
; 
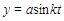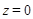, где x и y в м,
а t - в с.
1. Определить траекторию точки и построить её на чертеже. Указать на ней положения точки в заданные моменты времени, обозначить их 
и 
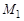( – в момент времени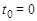 
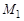; – в момент 
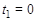с) - pис. 1.4. Исключив параметр 
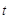из уравнений, получим
.
Так как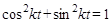 
, то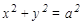 
- это уравнение окруж-ности с радиусом 
.
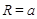При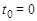
 |
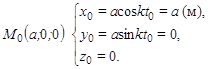
Рис. 1.4
При 
с,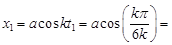 
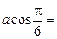
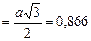а (м),
,
.
; 
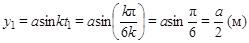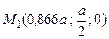, так как 
.
2. Для момента времени 
определить и построить на чертеже:
- скорость точки :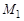
,
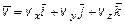(м/с),
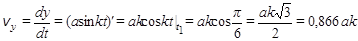(м/с),
,
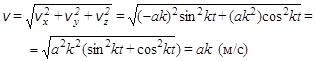
- модуль вектора скорости.
Направляющие косинусы вектора скорости:
,
,
.
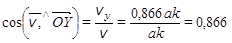- ускорение точки :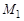
,
.
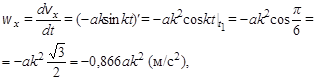
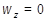Модуль вектора ускорения точки :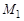
|
|
.
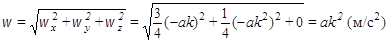Направляющие косинусы вектора ускорения точки:
,
,
.
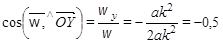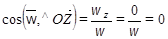3. Определить касательное и нормальное ускорения точки 
,
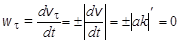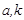- постоянные величины;
,
.
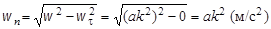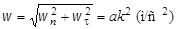Полное ускорение точки 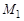равно нормальному ускорению, так как скорость по величине постоянна: 
.
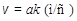4. Определить характер движения точки: точка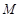 
движется по окружности равномерно!
5. Определить радиус кривизны траектории точки в момент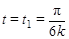 
:
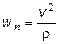- нормальное ускорение;
отсюда
- радиус окружности траектории точки .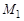
З А Д А Н И Е К2
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ВОКРУГ (ОКОЛО) НЕПОДВИЖНОГО ПОЛЮСА
Цель – определить кинематические элементы: векторы угловой скорости, углового ускорения абсолютно твердого тела при его вращении вокруг неподвижного полюса, а также векторы скоростей и ускорений некоторых точек тела при указанном движении.