Задача сформулирована отдельно для каждого варианта, чертежи к задачам помещены на схемах, необходимые данные –
в таблице «Исходные данные», с. 33-36 (кроме вариантов, отмеченных звездочкой, с №№ 14, 15, 18, 19, 20, которые содержат исходные данные в условии задачи). Во всех вариантах рассматривается регулярная прецессия твердого тела.
1. Найти неподвижную точку вращения тела, выбираемую за начало отсчета неподвижной (инерциальной) и связанной коорди-натных систем. Выбрать оси прецессии  , ротации
, ротации  .
.
2. Определить угловые скорости нутации, прецессии, ротации, мгновенную угловую скорость  и мгновенную ось вращения
и мгновенную ось вращения  . В зависимости от движения твёрдого тела вектор
. В зависимости от движения твёрдого тела вектор  можно найти двумя путями: 1) определением
можно найти двумя путями: 1) определением  по ее составляющим (2.1);
по ее составляющим (2.1);
2) использованием мгновенной оси вращения.
По известной скорости 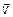 какой-либо точки М твердого тела и положению оси
какой-либо точки М твердого тела и положению оси  найти величину
найти величину 
 , где
, где  - кратчайшее расстояние от точки М до мгновенной оси
- кратчайшее расстояние от точки М до мгновенной оси  .
.
3. Определить угловое ускорение  твердого тела. Как известно,
твердого тела. Как известно,  , где точка k – конец вектора
, где точка k – конец вектора  . В случае регулярной прецессии
. В случае регулярной прецессии  является закрепленным в точке О векто-ром и определяется по формуле (2.2).
является закрепленным в точке О векто-ром и определяется по формуле (2.2).
4. Определить скорости произвольных точек твёрдого тела по формуле (2.3).
5. Определить ускорения произвольных точек твёрдого тела. Ускорение  любой точки твёрдого тела определить по формуле
любой точки твёрдого тела определить по формуле  , где осестремительное ускорение определяется по (2.4), а его величина
, где осестремительное ускорение определяется по (2.4), а его величина  , вращательное ускорение - по (2.5), его величина
, вращательное ускорение - по (2.5), его величина 
Так как  всегда направлено по
всегда направлено по  к оси
к оси  , можно не пользоваться векторной формой для
, можно не пользоваться векторной формой для  . Наоборот,
. Наоборот,  следует находить только в векторной форме.
следует находить только в векторной форме.
Поскольку при вращении около полюса (в отличие от вращения около неподвижной оси)  не коллинеарен
не коллинеарен  , то
, то  и
и  , вообще говоря, не являются перпендикулярными векторами. Поэтому
, вообще говоря, не являются перпендикулярными векторами. Поэтому  следует находить после построения векторов на чертеже, и величина ускорения будет определяться по (2.6).
следует находить после построения векторов на чертеже, и величина ускорения будет определяться по (2.6).
Для точек, лежащих на оси ротации твёрдого тела, справедливы и следующие зависимости:
 и
и 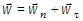 ,
,
где  - нормальное ускорение;
- нормальное ускорение;  - касательное ускорение; при регулярной прецессии
- касательное ускорение; при регулярной прецессии  ;
;  - кратчайшее расстояние от точки, лежащей на оси ротации, до оси прецессии
- кратчайшее расстояние от точки, лежащей на оси ротации, до оси прецессии  .
.
Задание выполняется с приведением эскизных чертежей. Величины, приводимые в таблицах «Исходные данные», считаются точными. Все векторы, лежащие в плоскости xOy (плоскости чертежа), должны быть изображены в этой плоскости; направление других векторов должно быть указано в тексте.
Варианты заданий (условия задач)
Вариант 1.
Прямой круговой конус с углом 2α при вершине катится по плоскости без скольжения таким образом, что ускорение точки С – центра основания конуса – направлено по нормали к ее траектории и равно постоянной величине  . Высота конуса
. Высота конуса  .
.
Определить:
1) алгебраические величины проекций угловых скоростей прецессии, ротации и мгновенной угловой скорости на оси  ,
,  ,
,  соответственно;
соответственно;
2) угловое ускорение конуса;
3) скорости точек А, В и С;
4) ускорения точек А и В (чему равен  , составленный векторами
, составленный векторами 
 ).
).
Вариант 2.
Прямой круговой усеченный конус катится без скольжения по неподвижной горизонтальной плоскости. Высота конуса  , радиусы большого и малого оснований равны R и r.
, радиусы большого и малого оснований равны R и r.
Движение конуса происходит так, что скорость центра большего основания постоянна и равна  .
.
Определить:
1) алгебраические величины проекций угловых скоростей прецессии, ротации и мгновенной угловой скорости на оси  ,
,  ,
,  соответственно;
соответственно;
2) алгебраическую величину проекции углового ускорения на ось  ;
;
3) скорости точек А и В;
4) ускорения точек В и С.
Вариант 3.
Прямой круговой конус с углом 2α при вершине катится без скольжения по неподвижной плоскости, делая n оборотов в минуту около вертикальной оси  . Высота конуса
. Высота конуса  .
.
Определить:
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси  и
и  соответственно, а также мгновенную угловую скорость конуса;
соответственно, а также мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорости точек В и С;
4) ускорение точки В, а также осестремительное и вращатель-ное, нормальное и касательное ускорения точки С.
Вариант 4.
Конус 1 с углом 2α при вершине катится без скольжения
по неподвижному конусу 2 с углом 2β при вершине. Высота конуса  . Движение конуса происходит так, что осестремительное ускорение центра С основания конуса
. Движение конуса происходит так, что осестремительное ускорение центра С основания конуса 
постоянно и равно 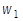 .
.
Определить:
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси  и
и  , соответственно, и мгновенную угловую скорость конуса;
, соответственно, и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) ускорения точек В и С (найти вращательное, а также нормальное и касательное ускорения точки С).
Вариант 5.
Конус 1 с углом 2α при вершине катится без скольжения по неподвижному конусу 2 с углом 2β при вершине так, что скорость точки С центра основания конуса постоянна и равна  ,
,  в данный момент времени. Высота конуса
в данный момент времени. Высота конуса  .
.
Определить:
1) угловую скорость прецессии, нутации и ротации и мгновенную угловую скорость конуса 1;
2) угловое ускорение конуса;
3) скорости точек А и В;
4) ускорения точек А и С (найти нормальное и осестреми-тельное ускорения точки С).
Вариант 6.
Прямой круговой конус 1 с углом 2α при вершине катится без скольжения по неподвижному конусу 2, обегая его n раз в минуту. Угол при вершине неподвижного конуса равен 2β, радиус основания конуса 1 равен R.
Определить:
1) угловые скорости прецессии, нутации, ротации и мгновенную угловую скорость конуса 1;
2) алгебраическую величину проекции углового ускорения конуса на ось  в данный момент времени;
в данный момент времени;
3) скорости точек В и С;
4) ускорение точки С – центра основания конуса. Указать нормальную и касательную составляющие, а также вращательное и осестремительное ускорения точки С. Какой угол γ составляют между собой  и
и  ?
?
Вариант 7.
Конус 1 с углом 2α при вершине катится без скольжения по неподвижному конусу 2 с углом 2β при вершине, совершая за время Т один оборот вокруг вертикальной оси  против часовой стрелки. Высота конуса
против часовой стрелки. Высота конуса  .
.
Определить:
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси  и
и  соответственно и мгновенную угловую скорость конуса;
соответственно и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) полное ускорение точки А; вращательное и осестремительное ускорения точки С; какой угол составляют между собой эти векторы?
Вариант 8.
Прямой круговой конус 1 высотой  с углом при вершине 2α равномерно катится без скольжения по неподвижному конусу 2 с углом при вершине 2β. Вращательное ускорение центра основания конуса
с углом при вершине 2α равномерно катится без скольжения по неподвижному конусу 2 с углом при вершине 2β. Вращательное ускорение центра основания конуса  .
.
Определить:
1) угловое ускорение конуса;
2) угловые скорости прецессии и ротации и мгновенную угловую скорость конуса;
3) скорости точек В и С;
4) осестремительное и полное ускорение точки С, а также касательную и нормальную составляющие ускорения этой точки.
Вариант 9.
Прямой круговой конус 1 высотой  с углом при вершине 2α равномерно катится без скольжения по неподвижному конусу 2 с углом при вершине 2β. Ускорение точки М конуса, лежащей на середине его образующей, равно:
с углом при вершине 2α равномерно катится без скольжения по неподвижному конусу 2 с углом при вершине 2β. Ускорение точки М конуса, лежащей на середине его образующей, равно: 
 .
.
Определить:
1) угловое ускорение конуса;
2) угловые скорости прецессии, ротации и мгновенную угловую скорость конуса;
3) скорости точек С и В;
4) ускорение точки С и точки N, лежащей на середине обра-зующей ОВ.
Вариант 10.
Прямой круговой конус 1 с углом при вершине 2α и радиусом основания R перекатывается без скольжения по неподвижному конусу 2 с углом при вершине 2β. Подвижный конус совершает n оборотов в минуту вокруг своей оси симметрии  .
.
Определить:
1) угловые скорости прецессии, нутации и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорости точек В и С;
4) вращательное, осестремительное и полное ускорения точки С, а также ее касательное и нормальное ускорения; ускорение точки А.
Вариант 11.
Прямой круговой конус 1 с углом при вершине 2α и радиусом основания R перекатывается без скольжения по неподвижному конусу 2 с углом при вершине 2β. Центр основания конуса С описывает полную окружность 90/π раз в минуту.
Для данного положения конуса (сечение OAB совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорости точек A и B;
4) ускорение точки С (указать нормальную и касательную составляющие, а также вращательное и осестремительное ускорения точки С). Определить угол γ, который составляют между собой 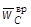 и
и  .
.
Вариант 12.
Прямой круговой конус 1 высотой  с углом 2α при вершине равномерно катится без скольжения по внутренней поверхности конуса 2 с углом 2β при вершине. Ускорение точки М, лежащей на половине образующей ОА, равно:
с углом 2α при вершине равномерно катится без скольжения по внутренней поверхности конуса 2 с углом 2β при вершине. Ускорение точки М, лежащей на половине образующей ОА, равно: 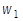
 .
.
Определить:
1) Угловые скорости прецессии, нутации, ротации и мгновенную угловую скорость конуса;
2) Угловое ускорение конуса;
3) Скорости точек А, В и С;
4) Ускорения точек В и С.
Вариант 13.
Прямой круговой конус 1 с углом 2α при вершине и радиусом основания R катится без скольжения по внутренней поверхности неподвижного конуса 2 с углом 2β при вершине. Скорость точки С основания конуса постоянна и равна  ;
;  в данный момент времени.
в данный момент времени.
Определить:
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси  и
и  соответственно и мгновенную угловую скорость конуса;
соответственно и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) ускорение точки А;
5) ускорение точки N, лежащей на середине образующей ОВ конуса. Под каким углом γ к образующей конуса ОВ направлен вектор  ?
?
Вариант 14.
Конический каток равномерно вращается вокруг полюса О так, что точка С описывает окружность со скоростью  = 2 м/с. Размеры катка: ОС = СА = СВ = 2 м, СK = KM = KN = 1 м.
= 2 м/с. Размеры катка: ОС = СА = СВ = 2 м, СK = KM = KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угол нутации, угловые скорости прецессии, ротации и мгновенную угловую скорость катка;
2) угловое ускорение катка;
3) скорости точек A и B;
4) ускорение точек N и C (найти также вращательную и осестремительную, нормальную и касательную составляющие ускорения точки С).
Вариант 15.
Конический каток равномерно вращается вокруг полюса О так, что точка C описывает окружность за π с. Размеры катка: OC = CA = CB = 2 м, CK = KM = KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации и мгновенную угловую скорость катка.
2) угловое ускорение катка.
3) скорости точек В и N.
4) ускорения точек M и C (найти также вращательную и нормальную составляющие ускорения точки С).
Вариант 16.
Коническая зубчатая шестерня радиуса r, находясь в зацеплении с плоской неподвижной шестерней радиуса R, движется таким образом, что величина ускорения центра С шестерни постоянна и равна  .
.
Определить:
1) угловые скорости прецессии, ротации, нутации и мгновенную угловую скорость шестерни;
2) угловое ускорение шестерни;
3) скорости точек А, В и С;
4) ускорения точек А и В.
Вариант 17.
Кривошип ОС равномерно вращается против часовой стрелки около вертикальной оси  , делая n оборотов в минуту. В точке С на него свободно насажена коническая шестерня радиуса r, перекатывающаяся по зубчатому основанию радиуса R.
, делая n оборотов в минуту. В точке С на него свободно насажена коническая шестерня радиуса r, перекатывающаяся по зубчатому основанию радиуса R.
Пренебрегая высотой зубьев, определить:
1) алгебраические величины проекций угловых скоростей прецессии, ротации и мгновенной угловой скорости шестерни на оси  ,
,  и
и  соответственно;
соответственно;
2) угловое ускорение шестерни;
3) скорости точек А и В;
4) ускорения точек С и В.
Вариант 18.
Конический каток равномерно вращается вокруг полюса О, имея скорость в центре основания конуса в точке С  = 2 м/с. Размеры конуса: ОС = СА = СВ = 2 м, СK = KM = KN = 1 м.
= 2 м/с. Размеры конуса: ОС = СА = СВ = 2 м, СK = KM = KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации и мгновенную угловую скорость катка;
2) угловое ускорение катка;
3) скорости точек B и K;
4) ускорение точек M и С.
Вариант 19.
Конический каток равномерно вращается вокруг полюса О так, что точка C описывает окружность за π с. Размеры катка: OC = CA = CB = 2 м, CK = KM = KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации и мгновенную угловую скорость катка;
2) угловое ускорение катка;
3) скорости точек N и B;
4) ускорения точек B и C (указать величины составляющих ускорений точки С:  ,
,  ).
).
Вариант 20.
Конический каток равномерно вращается вокруг полюса О, имея скорость в центре С основания конуса  = 2 м/с. Размеры конуса: OC = CA = CB = 2 м, CK = KM = KN = 1 м.
= 2 м/с. Размеры конуса: OC = CA = CB = 2 м, CK = KM = KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации, нутации и мгновенную угловую скорость катка;
2) угловое ускорение катка;
3) скорости точек N и C;
4) ускорения точек B и C.
Исходные данные
| № вар | 2α | 2β | h | r | R | vС | w 1 | n | T |
| град | м | м/с | м/с2 | об/мин | с | ||||
| - | 0,12 | - | - | - | 0, 
| - | - | ||
| - | 0,12 | - | - | - | 0, 
| - | - | ||
| - | 0,10 | - | - | - | 0, 
| - | - |
| № вар. | 2α | 2β | h | r | R | vC | w 1 | n | T |
| град | м | м/с | м/с2 | об/мин | с | ||||
| - | - | 0,40 | 0,40 | 0,80 | 2,00 | - | - | - | |
| - | - | 0, 
| 0,30 | 0,50 | 
| - | - | - | |
| - | - | 0,50 | 0,50 | 1,00 | 1,00 | - | - | - | |
| - | 0,20 | - | - | - | - | - | |||
| - | 0,40 | - | - | - | - | - | |||
| - | 0,30 | - | - | - | - | - | |||
| 0,18 | - | - | - | 0,36 | - | - | |||
| 0,16 | - | - | - | 0,32 | - | - | |||
| 0,15 | - | - | - | 0,30 | - | - | |||
| 0,10 | - | - | 0,20 | - | - | - | |||
| 0.15 | - | - | 0,45 | - | - | - | |||
| 0,20 | - | - | 0,80 | - | - | - | |||
| - | - | 0,30 | - | - | 30/π | - | |||
| - | - | 0,25 | - | - | 60/π | - | |||
| - | - | 0,20 | - | - | 90/π | - | |||
| 0,20 | - | - | - | - | - | ||||
| 0,30 | - | - | - | - | - | ||||
| 0,40 | - | - | - | - | - |
| № вар. | 2α | 2β | h | r | R | VC | w 1 | n | T |
| град | м | м/с | м/с2 | об/мин | с | ||||
| 0,12 | - | - | - | 0, 
| - | - | |||
| 0,16 | - | - | - | 0, 
| - | - | |||
| 0,20 | - | - | - | 0, 
| - | - | |||
| 0,12 | - | - | - | 0,48 | - | - | |||
| 0,16 | - | - | - | 0,72 | - | - | |||
| 0,20 | - | - | - | 0,80 | - | - | |||
| - | - | 0,18 | - | - | - | ||||
| - | - | 0,24 | - | - | - | ||||
| - | - | 0,30 | - | - | - | ||||
| - | - | 0,10 | 0,30 | - | - | - | |||
| - | - | 0,12 | 0,36 | - | - | - | |||
| - | - | 0,14 | 0,42 | - | - | - | |||
| 0,12 | - | - | - | 0,24 | - | - | |||
| 0,15 | - | - | - | 0,30 | - | - | |||
| 0,18 | 0,36 | - | |||||||
| - | - | 0,12 | 0, 
| - | - | - | |||
| - | - | 0,15 | 0, 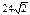
| - | - | - | |||
| - | - | 0,18 | 0, 
| - | - | - | |||
| 14* | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| 15* | - | - | |||||||
| - | |||||||||
| - | - | - | - |
| № вар. | 2α | 2β | h | r | R | vC | w 1 | n | T |
| град | м | м/с | м/с2 | об/мин | с | ||||
| 0,20 | 0,40 | - | 0,90 | - | - | ||||
| - | - | - | 0,30 | 0,60 | - | 1,20 | - | - | |
| - | - | - | 0,20 | 0, 
| - | 0,60 | - | - | |
| - | - | - | 0,10 | 0, 
| - | - | - | ||
| - | - | - | 0,15 | 0, 
| - | - | - | ||
| - | - | - | 0,20 | 0, 
| - | - | - | ||
| 18* | |||||||||
| 19* | |||||||||
| 20* | |||||||||
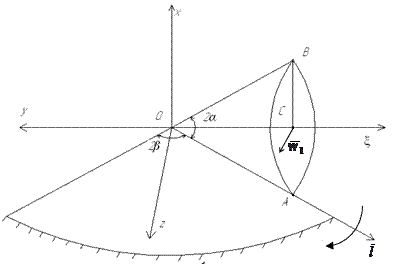
Рисунки к вариантам 1-20
Стр. 37-41
 |
П р и м е р. Конус 1 с углом 2a при вершине катится без скольжения (в указанном стрелкой направлении) по неподвижному конусу с углом 2b при вершине. Высота конуса 1 OC = h. Движение конуса происходит так, что осестремительное ускорение центра С основания конуса
 постоянно и равно
постоянно и равно 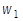 . Исходные данные - в таблице и на рис. 2.5.
. Исходные данные - в таблице и на рис. 2.5.
Рис. 2.5
Определить:
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси  , и
, и  соответственно и мгновенную угловую скорость конуса;
соответственно и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) ускорение точек В и С (найти вращательное, а также нормальное и касательное ускорения точки С).
Исходные данные: 
 0,36 м/с2.
0,36 м/с2.
Решение. Осестремительное ускорение точки С определяется по формуле (2.4)  , а модуль вектора
, а модуль вектора  , где w - мгновенная угловая скорость конуса, а
, где w - мгновенная угловая скорость конуса, а  - расстояние по перпендикуляру от точки С до мгновенной оси вращения конуса
- расстояние по перпендикуляру от точки С до мгновенной оси вращения конуса  , (pис. 2.6). На рисунке
, (pис. 2.6). На рисунке 
 .
.

Рис. 2.6
Тогда можно определить
 ,
,  .
.
Стрелка на pис. 2.6 указывает, что вращение конуса 1 происходит по ходу часовой стрелки, если смотреть с положительного конца оси прецессии  , поэтому
, поэтому  противоположна по направлению оси
противоположна по направлению оси  .
.
2. Далее по теореме синусов для векторного треугольника OMP (см. рис. 2.6) можно записать:
 . (2.7)
. (2.7)
Векторный треугольник построен так, что  (оси прецессии), а
(оси прецессии), а  (оси ротации),
(оси ротации),  (мгновенной оси вращения).
(мгновенной оси вращения).
Из (2.7)
 ,
,
 .
.
Определили угловые скорости прецессии 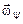 и ротации
и ротации  , соответственно, причем
, соответственно, причем  .
.
Проанализируем результат:
 (2.8)
(2.8)
Имеем регулярную прецессию, так как выполняется условие (2.8).
3. При регулярной прецессии вектор углового ускорения конуса  определяется по формуле (2.3)
определяется по формуле (2.3)  .
.
Величину углового ускорения конуса определить по формуле
 ,
,
 (см. рис. 2.6).
(см. рис. 2.6).
Вектор углового ускорения  ; в силу (2.2)
; в силу (2.2) 
4. Вектор скорости точки В определяется по формуле (2.3):  .
.
Тогда величина вектора скорости  , где
, где  - кратчайшее расстояние от точки В до мгновенной оси вращения
- кратчайшее расстояние от точки В до мгновенной оси вращения  .
.

Вектор скорости точки В по направлению совпадает с осью 
 (см. формулу (2.3)).
(см. формулу (2.3)).
5. Вектор ускорения точки В определить по формуле  как векторную сумму осестремительного и вращательного ускорений точки В.
как векторную сумму осестремительного и вращательного ускорений точки В. 
 (м/с2) - величина осестремительного ускоре-
(м/с2) - величина осестремительного ускоре-
ния точки В. (направление всегда известно по наименованию
(см. рис. 2.6)).
Вектор вращательного ускорения 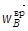 определить из
определить из
векторного произведения (2.5)  , тогда
, тогда 

 (м/с2).
(м/с2).
Вектор  и направлен в силу (2.5), как показано на рис. 2.6.
и направлен в силу (2.5), как показано на рис. 2.6.
Полное ускорение точки В, вектор  определить по теореме косинусов (2.6):
определить по теореме косинусов (2.6):  . Угол
. Угол  =60°, cos60°=0,5.
=60°, cos60°=0,5.
Тогда  (м/с2) (с точностью до трех значащих цифр).
(м/с2) (с точностью до трех значащих цифр).
Направление вектора  (см. рис. 2.6) построить как диагональ параллелограмма со сторонами
(см. рис. 2.6) построить как диагональ параллелограмма со сторонами  . Обратить внимание на то, что угол между
. Обратить внимание на то, что угол между  не равен 90°, как это бывает при вращении тела вокруг неподвижной оси.
не равен 90°, как это бывает при вращении тела вокруг неподвижной оси.
6. Точка  , поэтому вектор ускорения
, поэтому вектор ускорения  можно определить как векторную сумму касательного
можно определить как векторную сумму касательного  и нормального
и нормального  ускорений точки С, т.е.
ускорений точки С, т.е. 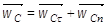 .
.
Касательное ускорение 
 м/с2 = const,
м/с2 = const,  , расстояние от точки С до оси
, расстояние от точки С до оси  ,
,  .
.
Тогда вектор ускорения точки С совпадает с ее нормальным ускорением  , а величина
, а величина 
= 0,18 (м/с2),  м/с2 - ускорение точки С (см. pис. 2.6).
м/с2 - ускорение точки С (см. pис. 2.6).
Вектор  , направлен к центру О окружности радиуса
, направлен к центру О окружности радиуса  , по которой движется точка С в результате прецессии.
, по которой движется точка С в результате прецессии.
Вращательное ускорение точки С определить по формуле (2.5) векторного произведения  .
.
Величина  (м/с2),
(м/с2),  =
= 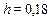 м.
м.
Вектор  и направлен, как на рис. 2.6, - см. форму-
и направлен, как на рис. 2.6, - см. форму-
лу (2.5).
З А Д А н и е К3