К кинематическим характеристикам твердого тела, вращаю-щегося вокруг (около) неподвижного полюса, относятся угловая скорость 
и угловое ускорение 
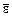. Угловой скоростью вращения твердого тела вокруг (около) неподвижного полюса называется векторная физическая величина, изображаемая закрепленным вектором, имеющим начало в неподвижном полюсе, и полностью характеризующая вращение данного тела вокруг (около) этого полюса. В проекциях на оси ротации, прецессии и нутации (рис. 2.2) угловая скорость записывается в виде
,
где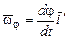 
– угловая скорость ротации или собственного вращения; 
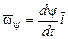– угловая скорость прецессии; 
– угловая скорость нутации; 
– орты осей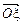 
(ротации), 
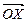(прецессии), 
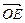(нутации), соответственно.
П р и м е ч а н и е: 
– орты неподвижной системы координат Oxyz, 
- орты связанной системы координат Oξηζ.
 |
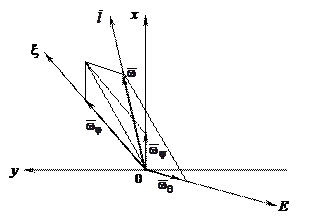Рис. 2.2
Величина и направление угловой скорости определяются по алгебраическим величинам ее проекций на оси:
- неподвижной системы координат Oxyz:
;
; (2.1)
;
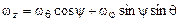- связанной системы координат Oξηζ:
;
;
.
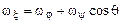Величина угловой скорости
,
ее направление в системе координат Oxyz определяется направ-ляющими косинусами:
, 
, 
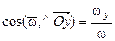(аналогично определяется направление в системе координат Oξηζ).
Ось, проходящая через неподвижный полюс и коллинеарная с вектором угловой скорости твердого тела, называется мгновенной осью вращения твердого тела. Уравнение мгновенной оси вращения в системе координат Oxyz
,
в системе координат Oξηζ
.
Коническая поверхность с вершиной в неподвижной точке, представляющая геометрическое место мгновенных осей враще-ния в неподвижной системе координат Oxyz, называется непод-вижным аксоидом, в подвижной системе координат Oξηζ – подвижным аксоидом.
|
|
Угловым ускорением твердого тела, вращающегося около неподвижного полюса, называется векторная физическая вели-
чина, изображаемая закрепленным вектором, имеющим начало
в этом полюсе, и характеризующая изменение угловой скорости
в данный момент времени как по величине, так и по направле-
нию.
Вектор углового ускорения тела определяется как первая производная вектора угловой скорости по времени: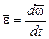 
.
Величина и направление углового ускорения могут быть
найдены через алгебраические величины проекций на оси коорди-
нат:
, 
, 
,
здесь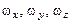 
определяются по формулам (2.1):
,
направление вектора 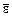определяется направляющими косинусами углов:
, 
, 
.
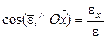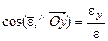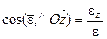П р и м е ч а н и е. Аналогично можно было бы определить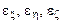 
.
Частный случай – регулярная прецессия – вращение твердого тела около неподвижного полюса, при котором во все время движения остаются постоянными угол нутации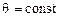 
и величины угловых скоростей прецессии (
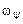) и собственного вращения (ротации) (
):
, 
, 
.
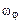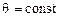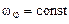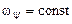В этом случае абсолютная величина угловой скорости
и вектор во все время движения находится в плоскости нутации xOξ (рис. 2.3).
Угловое ускорение 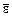определяется формулой
, (2.2)
 |
а его линия действия во все время движения твердого тела будет совпадать с линией узлов (осью нутации)
.
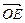Рис. 2.3