КИНЕМАТИКА
Контрольные задания
для выполнения расчетных
и курсовых работ
Министерство образования и науки Российской Федерации
Балтийский государственный технический университет «Военмех»
КИНЕМАТИКА
Контрольные задания
для выполнения расчетных
и курсовых работ
Под редакцией Г.Т. Алдошина
Санкт- Петербург
Составители: Т.Н. Рябинина, канд. техн. наук, доц. (задания К1
и К2); Н.Е. Рупасова, канд. техн. наук, доц. (задания К3 и К4)
УДК 531.1(075:8)
|
 |
К41
УДК 531.1(075:8)
Р е ц е н з е н т канд. техн. наук, проф. В.Ф. Федоров
Утверждено
редакционно-издательским
советом университета
© БГТУ, 2011
© Составители, 2011
 |
Общие требования к оформлению
расчетной работы
1. Работа должна содержать сформулированное (в соответствии с номером варианта) задание с указанием данных величин и искомых параметров.
2. Чертежи и графики к задачам должны быть четкими и ясными. Там, где это требуется, необходимо соблюдать масштаб, указывая его.
3. Решение должно быть полным и обоснованным.
4. Числовые расчеты проводятся с точностью до трех значащих цифр.
5. Образец титульного листа расчетной (курсовой) работы приведен в приложении.
6. Расчетная работа должна быть оформлена в соответствии с указанными требованиями. Небрежно оформленные работы к защите не принимаются.
7. Срок приема расчетной работы определен учебным графиком, разработанным деканатом по согласованию с кафедрой.
8. При защите расчетной работы студент обязан ответить на любой вопрос по теории или методам решения задач, относящийся к теме работы.
З А Д А Н И Е К1
КИНЕМАТИКА ТОЧКИ
Цель – определить положение точки относительно выб-ранной системы отсчета в заданный момент времени, а также векторы скорости и ускорения точки и радиус кривизны траектории в тот же момент времени:
1. Определить и построить на чертеже траекторию точки, показав на ней ее положении в начальный момент времени (t = 0) и в момент времени (t = t 1).
2. Для момента времени t = t 1определить и построить на чертеже:
- скорость и ускорение точки;
- касательное и нормальное ускорения.
3. Установить характер движения точки (ускоренное, замед-ленное).
4. Определить радиус кривизны траектории точки в момент времени t = t 1.
Краткие сведения из теории
Определение положения точки
1. При векторном способе задания (рис. 1.1, а) - ее радиусом-вектором как функцией времени: 
- кинематическое уравнение движения точки;
2. При координатном способе задания (рис. 1.1, б) – ее коор-динатами как функциями времени:
(1.1)
- кинематические уравнения движения точки в декартовых координатах;
3. При траекторном способе задания (рис. 1.1, в) – ее траекторной координатой (дугой) s, отсчитываемой от выбранного начала отсчета траекторных координат и зависящей от времени:
(1.2)
- кинематическое уравнение движения точки в траекторной форме.
 |
Для получения уравнения траектории, по которой движется точка, следует исключить параметр времени t из кинематических уравнений движения точки в координатной форме (1.1). При этом следует установить область изменения координат x, y, z с траектор-ной координатой s:
,
где s 0 - начальное значение траекторной координаты s.
Определение скорости точки
1. При координатном способе задания движения точки – урав-нение (1.1). Разложение вектора скорости по осям декартовой системы координат имеет вид
,
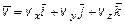где 
- орты осей декартовых координат.
Компоненты вектора скорости представляют собой произ-водные соответствующих координат точки:
.
Абсолютная величина скорости 
.
Направление вектора скорости определяется ее направ-ляющими косинусами:
.
2. При траекторном способе задания движения точки. Известно кинематическое уравнение движения точки в траекторной форме: s = f (t).
Скорость точки в данный момент времени определяется по формуле
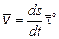или 
,
где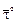 
- орт касательной к траектории в данной точке, направленной в сторону увеличения траекторных координат,
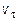- алгебраическая величина проекции скорости на касатель-
ную:
.
Скорость точки всегда направлена по касательной в данной точке траектории в сторону движения точки. Если 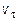> 0, то точка движется в сторону возрастания траекторной координаты s, 
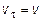(рис. 1.2, а), а при 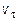< 0 - в сторону убывания значений s, 
(рис. 1.2, б).
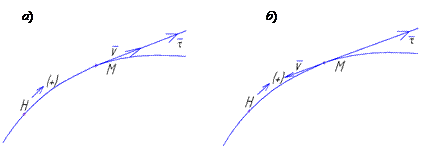
Рис. 1.2
Определение ускорения точки
1. При координатном способе задания движения - уравнение (1.1). Разложение вектора ускорения точки по осям декартовой системы координат имеет вид
.
Компоненты вектора ускорения представляют собой произ-водные соответствующих компонент вектора скорости или вторые производные соответствующих координат точки:
.
Абсолютная величина ускорения - 
.
Направление вектора ускорения определяется направляющими косинусами:
.
2. При траекторном способе задания движения точки - уравнение (1.2). Ускорение точки в данный момент времени определяется как векторная сумма касательного и нормального ускорений:
.
Нормальное ускорение характеризует изменение скорости по направлению. Величина нормального ускорения определяется формулой
, (1.3)
где r - радиус кривизны траектории в данной точке.
Нормальное ускорение всегда направлено в сторону вогнутости траектории по нормали к траектории, к центру кривизны (рис. 1.3). Касательное ускорение характеризует изменение скорости по величине. Алгебраическая величина касательного ускорения равна:
.
При ускоренном движении касательное ускорение направлено в сторону скорости (рис. 1.3, а); при замедленном движении - в сторону, противоположную направлению скорости (рис. 1.3, б). Абсолютная величина ускорения равна:
.
Определение радиуса кривизны траектории точки
В том случае, когда движение задано координатным способом, радиус кривизны траектории определяется следующим образом:
- по формулам координатного способа задания движения (1.1) определяются скорость и полное ускорение точки:
;
- по формулам траекторного способа задания движения (1.2) определяются нормальное и касательное ускорения:
,
и далее - радиус кривизны траектории по формуле (1.3):
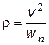. (1.4)