Текст задачи сформулирован в соответствии с номером варианта задания, чертежи к задаче (в соответствии с номером варианта) помещены на схеме, необходимые исходные данные – в таблице. Во всех вариантах система отсчета Oxyz является основной (неподвижной), ось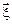 
принадлежит подвижной системе отсчета.
1. Установить относительное и абсолютное движения точки M. Установить переносное движение. Во всех вариантах данной задачи переносное движение является вращательным.
2. Изобразить рисунок согласно заданной строке числовых данных.
3. Определить кинематические величины (положение, скорость и ускорение) относительного движения точки. Для этого следует воспользоваться формулами задания К1.
При определении параметров относительного движения пере-носное движение мысленно останавливаем, т.е. считаем, что диск D или стержень AOB неподвижны.
Найти положение точки M для заданного момента времени t = t 1. Если в относительном движении точка движется по окружности (варианты 1–15), то нужно определить траекторную координату s. Отношение траекторной координаты к радиусу окружности R, по которой движется точка, дает угол ψ между прямыми OH и OM. Относительная скорость точки M определится по формуле
,
где 
– орт касательной в данной точке траектории, направлен-ный в сторону возрастания траекторной координаты.
Если 
, то 
, если 
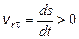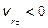, то 
.
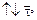Относительное ускорение точки M определить по формуле
,
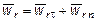где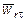 
– касательное (направлено по касательной к траектории), а 
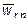– нормальное (направлено к точке O 1) ускорения точки:
, 
,
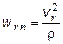где 
– радиус кривизны траектории в данной точке, r = R.
Все векторы определить в момент времени t = t 1 и изобразить на чертеже 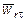и 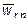(не определяя 
).
|
|
Если в относительном движении точка движется по прямой (варианты 16–25), то определить траекторную координату s и в зависимости от знака s отложить по оси 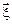отрезок длиной HM в направлении, совпадающем с 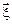или в противоположном.
Относительное ускорение = 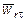, так как нормальное ускорение при движении точки по прямой равно нулю.
4. Определить кинематические величины (скорость и ускорение) точки в переносном движении. При определении параметров переносного движения относительное движение мысленно останавливаем.
Так как переносное движение является вращением твердого тела вокруг неподвижной оси, то можно использовать формулы соответствующего раздела кинематики.
Если по условию задачи задано уравнение вращательного движения диска или пластинки (варианты 1–10), то следует найти проекции угловой скорости и углового ускорения на ось вращения по формулам
, 
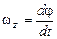для момента времени t = t 1.
Есл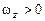и 
и 
, то векторы угловой скорости и углового ускорения направлены по оси вращения в сторону оси 
. При отрицательных значениях проекций векторы направлены в противоположную сторону.
Для вариантов 11–20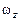 
и 
заданы по условию. Для вариантов 21–25 найти .
Переносная скорость точки M определится по формуле
,
где h – расстояние точки M до оси вращения тела D, w – модуль его угловой скорости.
Вектор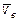 
направлен перпендикулярно радиусу вращения в сторону вращения тела, связанного с подвижной системой отсчета.
Переносное ускорение точки
,
где 
– осестремительное ускорение точки,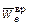 
– враща-тельное ускорение точки.
, 
.
– всегда направлено к оси вращения, 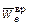– перпендикулярно радиусу вращения. Если 
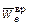
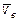, то , если 
,
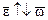то ¯ .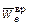
|
|
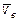Все векторы определить в момент времени t = t 1 и изобразить на чертеже 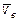, , 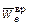(не определяя 
).
5. Определить направление вектора ускорения Кориолиса по формуле
и модуль ускорения Кориолиса 
. Если 
или один из векторов 
или обращается в ноль, то 
.
В противном случае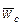 
перпендикулярен плоскости, проходящей через и , и направлен таким образом, чтобы поворот от к на кратчайший угол казался происходящим против хода часовой стрелки, если смотреть с конца резуль-тирующего вектора .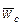
Определить 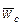в момент времени t = t 1 и изобразить 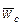на чертеже.
6. Определить скорость точки M относительно неподвижной системы координат (абсолютную скорость)
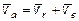. (4.1)
Если 
, то абсолютную скорость определять алгебраи-ческим сложением и 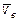, если 
, то по теореме Пифагора:
.
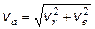В противном случае абсолютную скорость определять по теореме косинусов:
.
Абсолютное ускорение - по формуле
. (4.2)
Чтобы определить модуль абсолютного ускорения, нужно спроецировать равенство (4.2) на оси неподвижной системы координат и найти
.
Варианты заданий (условия задач)
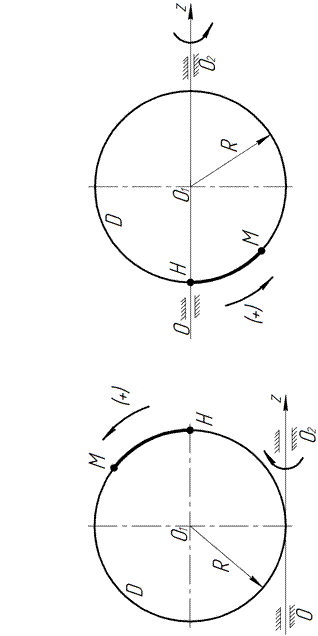
Варианты 1–5. Диск D вращается вокруг неподвижной оси так, что уравнение её вращательного движения имеет вид: 
, 
, где k – заданная постоянная величина.
По пластинке, по дуге ABC окружности радиусом R, движется точка M так, что траекторная координата этого движения изменяется согласно уравнению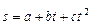 
, где a, b, c – заданные постоянные величины (траекторная координата отсчитывается от точки H). Определить скорость и ускорение точки M относительно неподвижной системы отсчёта Oxyz
в момент времени t = t 1.
|
|
Варианты 6–10. Диск D вращается вокруг неподвижной оси , перпендикулярной плоскости чертежа, так, что уравнение её вращательного движения имеет вид 
, .
По ободу диска движется точка M, траекторная координата этого движения, отсчитываемая от точки H, изменяется согласно уравнению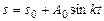 
, где s 0, A 0, k – заданные постоян-
ные величины. Определить скорость и ускорение точки M
в момент времени t = t 1 относительно неподвижной системы отсчёта Oxyz.
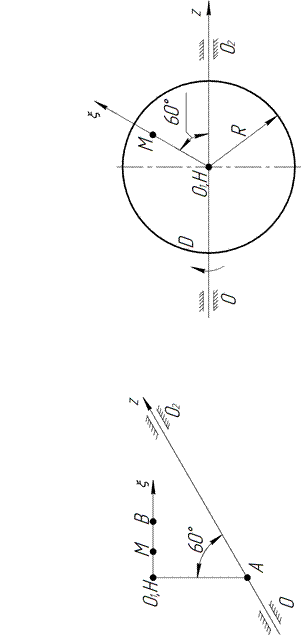
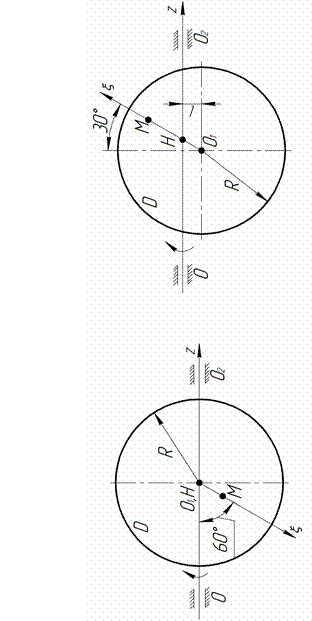
Варианты 11–15. По окружности диска D радиусом R движется точка M так, что траекторная координата s, отсчиты-ваемая от точки H изменяется согласно уравнению 
, где a и b – заданные постоянные величины. Диск D ускоренно (или замедленно) вращается вокруг неподвижной оси , расположенной в плоскости диска, имея в момент времени t 1 проекции на ось вращения угловой скорости 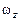и углово-
го ускорения . Определить скорость и ускорение точки M
в момент времени t = t 1 относительно неподвижной системы отсчета Oxyz.
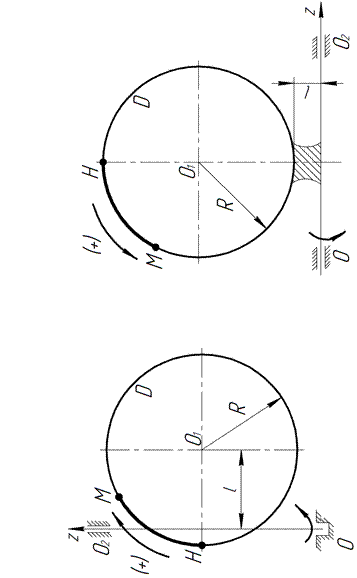
Варианты 16–20. Стержень AOB вращается ускоренно
(или замедленно) вокруг неподвижной оси , имея в момент времени t 1 проекции на ось вращения угловой скорости 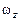и углового ускорения . По стержню движется точка M так, что уравнение её движения имеет вид: 
(отсчет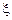 
производится от точки O), где 
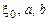– заданные постоянные величины. Определить скорость и ускорение точки M в момент времени t = t 1 относительно неподвижной системы отсчёта Oxyz.
Варианты 21–25. Диск D вращается вокруг неподвижной оси , расположенной в плоскости диска, с угловой скоростью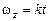 
рад/с. По радиусу диска в направлении оси 
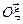движется точка M. Траекторная координата этого движения, отсчитываемая от точки H, изменяется согласно уравнению 
,
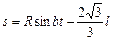где R, k, b, l – заданные постоянные величины. Определить скорость и ускорение точки M в момент времени t = t 1 относительно неподвижной системы координат Oxyz.
Исходные данные
| № вар. | a | l | R | k | b | c | t 1 |
| м | рад с-2 | м/с | м/с2 | с | |||
| 0,5 π -0,2 π | 4,0 2,0 1,6 | 2,0 1,0 0,8 | 0,007 0,5 π 0,5 | 0,1π 0,8 | -0,5 π 0,4 | 10,0 1,0 0,5 | |
| -0,8 π 0,2 π | 3,2 0,8 2,4 | 1,6 0,4 1,2 | 0,5 1,25 2,0 | 0,1π -0,6 π | 0,2 π 0,1π -1,2 π | 2,0 1,0 0,5 | |
| 0,2 π -0,8 π | 0,4 1,2 1,6 | 0,4 1,2 1,6 | 0,5 π 2,0 1,0 | 0,1π -0,6 π | 0,1π -1,2 π 0,2 π | 1,0 0,5 2,0 | |
| -0,6 π 1,2 π | - - - | 2,4 4,8 1,6 | 1,0 1,0 1/32 | 0,6π -1,2 π | 1,2 π 2,4 π π/60 | 1,0 1,0 4,0 | |
1,5
| 2,0 3,0 1,0 | 0,5 π 0,125 π 0,25 π | π -1,5 π 0,5 π | 1,0 1,0 1,0 |
| № вар. | a | R | l | b | ω z | ε z | t 1 |
| м | c-1 | рад/с | рад/с2 | с | |||
π
2 π
0,4π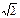 
| 2,0 4,0 1,2 | - - - | π/6 π/3 7π/4 | -1 -3 | -1,0 0,5 -1,0 | 1,0 0,5 1,0 | |
0,4π
0,6π
1,2π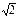 
| 0,6 1,2 2,4 | - - - | π/3 π/6 7π/4 | -4 | 1,0 -0,5 2,0 | 0,5 1,0 1,0 | |
3π 
1,2 π
1,5π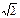
| 9,0 1,8 3,0 | 0,7 0,9 1,0 | π/3 π/2 7π/2 | -1 | -2,0 1,0 0,5 | 1,0 1/3 0,5 | |
| 0,6 π
1,6 π
0,8π
| 1,2 2,4 0,8 | 0,6 1,0 0,8 | π π/6 10π/3 | -4 -3 | 1,0 1,0 2,0 | 1/6 1,0 0,5 | |
| 1,6 π
5 π
2π
| 3,2 5,0 6,0 | 1,0 5,0 3,0 | π/3 π/6 10π/3 | -2 | 2,0 -1,0 1,0 | 0,5 1,0 0,5 |
| № вар. | l | R | S 0 | A 0 | k | α | t1 |
| м | с-1 | рад с-3 | с | ||||
3,6 
| 7,2 | 3,6 π | π/6 | 1/3 | 1,0 | ||
1,0
2,7 
| 2,4 5,4 | -1,2 π | 2,4 π 1,8 π | π/3 2π/3 |
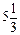
| 0,5 0,25 | |
| - - - | 6,0 1,8 3,6 | 3,5 π | 3,0π
0,4 π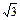 
0,8 π
| 11π/3 π/3 5π/3 | 2/3 | 0,5 1,0 1,0 | |
| 0,6
2,4
4,2
| 1,2 4,8 8,4 | -3,6 π | 0,6π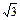
2,4 π
4,2 π
| π 0,5π π/3 | 4,5 1/25 | 1/3 2/3 | |
| - - - | 4,8 2,4 3,6 | 3,6 π | 2,4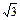π
1,2π
1,8π
| π π/3 11π/6 | 9/25 | 5/3 0,5 1,0 | |
| 2,25 1,8 4,0 | 4,5 3,6 8,0 | 6 π | 1,5π 1,2π 4π | π/6 11π/3 11π/6 | 1/3 | 1,0 0,5 1,0 |
| № вар. | a | AO | OB | ξ0 | b | ω z | εz | t 1 |
| м | с-1 | рад с-1 | рад с-2 | с | ||||
| 0,20 0,80 0,05 | 1,0 0,8 0,4 | 1,0 0,8 0,4 | -0,5 0,2 | π π/4 2π | 1,0 0,5 -0,5 | 0,5 -0,5 -1,0 | 1/3 2/3 4/3 | |
| 0,2 0,1 0,3 | 2,0 1,6 3,0 | 1,0 0,8 1,5 | 0,5 0,4 1,0 | π π/4 2 π | 2,0 -1,0 0,5 | 1,0 1,0 -1,0 | 1/3 2/3 4/3 | |
0,3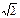
0,45 
0,5
| 1,2 1,8 2,0 | 0,6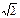
0,9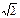
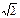
| 0,3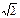
0,45
0,5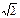
| 0,5 π 0,5 π 0,5 π | 2,0 0,5 4,0 | -1,0 -1,0 2,0 | 3,0 1,0 2,0 | |
| 0,5 0,8 0,6 | 0,4 0,6 0,8 | 1,0 1,6 1,2 | 0,5 0,8 0,6 | 3π π π/4 | 2,0 -2,0 0,5 | 1,0 2,0 -0,5 | 0,5 1,0 2,0 | |
| 0,2 0,3 0,2 | 0,8 /3
1,2
/3
| 1,2 1,2 0,5 | 0,4 0,6 0,2 | 3 π π π/2 | 3,0 -1,0 0,5 | 1,0 2,0 -0,5 | 0,5 1,0 1,0 |
| № вар. | R | l | b | k | t 1 |
| м | с-1 | рад c-2 | с | ||
| 2,0 4,0 1,2 | π/6 π/3 7π/4 | 1,0 0,5 1,0 | |||
| 0,6 1,2 2,4 | π/3 π/6 7π/4 | 0,5 1,0 1,0 | |||
| 9,0 1,8 3,0 |
0,3
0,5
| π/3 π/2 7π/2 | 1,0 1/3 0,5 | ||
| 1,2 2,4 0,8 | π π/6 10π/3 | 1/6 1,0 0,5 | |||
| 3,2 5,0 6,0 | 0,2
0,8
| π/3 π/6 10π/3 | 0,5 1,0 0,5 |
  |
  |
  |
  |
  |
  |
  |
  |
  |
  |
  |
  |
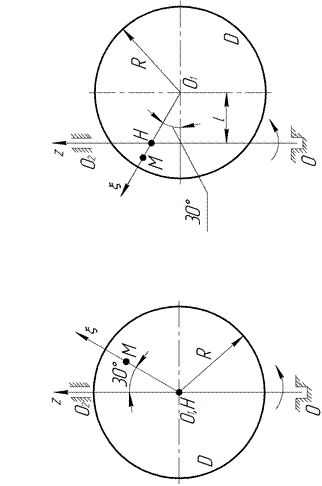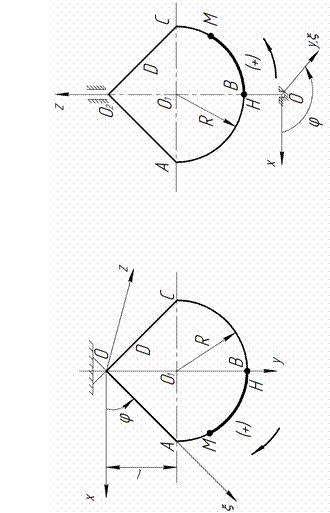
П р и м е р (см. рис. 4.1).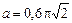 
м, R = 2,4 м, 
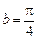с-1, 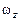= 2 рад/с, =- 1 рад/с2, t 1 = 1,0 с.
 |
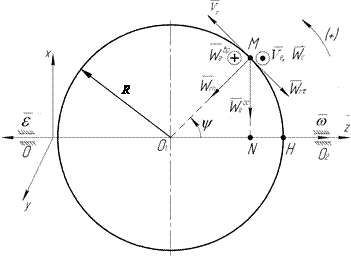Рис. 4.1
Определим положение точки M в заданный момент времени.
Траекторная координата при t = t 1:
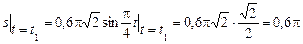м.
Найдем угол ψ, на который повернется радиус O 1 M из начального положения (O 1 H) в данное:
.
Изобразим текущее положение точки M.
1. Относительное движение – движение точки M по окружности радиуса R.
Относительная скорость точки M:
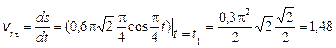м/с.
Так как проекция относительной скорости на направление касательной к траектории положительна, то вектор относительной скорости направлен по касательной к окружности в сторону положительного отсчета дуги.
Относительное ускорение при движении точки по окружности складывается из нормального и касательного ускорений:
.
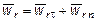Нормальное ускорение
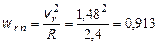м/с2.
Нормальное ускорение направляем к точке O 1 – центру окружности.
Касательное ускорение
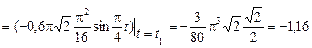м/с2.
Так как проекция относительного ускорения на направление касательной к траектории отрицательна, то вектор касательного ускорения 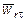направлен по касательной к окружности в сторону отрицательного отсчета дуги, т.е. относительное движение точки замедленное.
2. Переносное движение – вращение диска D вокруг неподвижной оси .
Так как 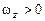, то вектор угловой скорости направлен в сторону оси ; так как 
, то вектор углового ускорения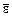 
направлен в сторону, противоположную оси , т.е. переносное движение замедленное.
Точка M перемещается по окружности радиусо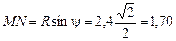м 
м.
Переносная скорость точки M
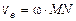
м/с.
Если смотреть с конца вектора , то диск D поворачивается против часовой стрелки, т.е. вектор переносной скорости 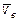направлен на нас.
Переносное ускорение точки M при вращении диска вокруг неподвижной оси складывается из осестремительного и вращательного:
.
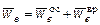Осестремительное ускорение
м/с2.
Вектор 
направлен по перпендикуляру MN к оси вращения .
Вращательное ускорение
м/с2.
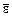Так как и направлены в противоположные стороны, то 
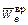направлено в сторону, противоположную 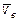, т.е. за чертеж.
3. Ускорение Кориолиса.
Направление вектора ускорения Кориолиса 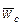определяется по формуле 
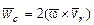, т.е. 
направлен перпендикулярно плоскости чертежа на нас. Величина ускорения Кориолиса опреде-ляется по формуле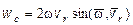 
= 4,19 м/с2.
4. Абсолютное движение – движение точки M относительно неподвижной системы отсчета Oxyz (сложное).
Абсолютная скорость
.
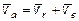Так как и 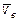взаимно перпендикулярны, то модуль абсолютной скорости определим по теореме Пифагора:
.
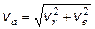Абсолютное ускорение
.
В нашей задаче
.
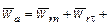
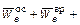
Проецируя это равенство на оси неподвижной системы координат Oxyz, получим:
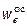
-8,27 м/с2;
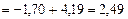м/с2;
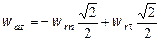
м/с2;
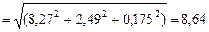м/с2. Строить векторы 
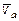и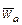 
на рисунке не нужно.