Тема 2.
Реализация случайного выбора.
- Реализация случайного выбора.
- Распределение качественных и количественных признаков.
- Выборочные характеристики и их свойства.
- Распределение выборочных характеристик.
Реализация случайного выбора.
Реализация эмпирической функции распределения.
Совокупность (Х1, Х2, …. Хп) п независимых случайных величин Хi, распределенных по одному и тому же закону, совпадающему с законом распределения случайной величины Х, называется выборкой объема п из генеральной совокупности Х (величины Хi представляют собой п экземпляров одной и той же случайной величины Х).
Если (Х1, Х2, …. Хп) – выборка, то последовательность чисел (х1, х2, …. хп) называется реализацией этой выборки.
Важнейшее значение для описания некоторой случайной переменной Х имеет функция распределения вероятностей F (Х) = 
.
Если функция распределения неизвестна, можно на основе реализации (Х1, Х2, …. Хп) выборки объема п из генеральной совокупности Х построить некоторое приближение к F(Х) с помощью функции 
, где n (x) – число значений Хi, меньших чем х). Эта функция представляет собой реализацию эмпирической функции распределения Wn(х).
Если (Х1, Х2, …. Хп) некоторая выборка, а (х1, х2, …. хп) – её реализация, тогда выборочная функция 
называется выборочным средним, а 
реализацией выборочного среднего.
Если выборка извлекается из генеральной совокупности случайной переменной Х с математическим ожиданием 
, тогда Е (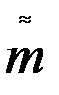
)= 
.
Реализация выборочной дисперсии составляет 
.
Если выборка извлекается из генеральной совокупности с математическим ожиданием 
и дисперсией
, тогда Е(
) = 
Статистическая оценка параметров.
Рассмотрим вопрос о том, как на основе некоторой выборки (Х1, Х2, …. Хп) найти оценку определенного параметра (например, математического ожидания или дисперсии) распределения случайной переменной Х.
Истинное значение некоторого параметра «а» обозначим через 
, его оценку с помощью некоторой выборочной функции через «
», а реализацию выборочной функции через 
.
1. Оценка = 
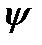(х1, х2, …, хп) некоторого параметра «а» называется симметричной, если выборочная функция 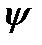(х1, х2, …, хп) является симметричной.
2. Оценка = 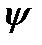(х1, х2, …, хп) некоторого параметра «а» называется несмещенной, если Е 
= .
3. Оценка = 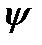(х1, х2, …, хп) некоторого параметра «а» называется состоятельной, если её значение при n 
0 с вероятностью 1 сходится к истинному значению , т.е. Р 
=1.
4. Оценка = 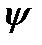(х1, х2, …, хп) некоторого параметра «а» называется эффективной, если среди всех других возможных оценок она обладает наименьшей дисперсией:
D () = Е 
= min.
Оценка 
для математического ожидания некоторой случайной переменной Х является симметричной, состоятельной и несмещенной, а для случая, когда величина Х распределена по нормальному закону, также и эффективной.
Оценка 
для дисперсии случайной переменной Х является симметричной, состоятельной и несмещенной, а в случае нормального распределения величины Х также и эффективной.
5. Пусть Х – нормально распределенная случайная величина, неизвестное математическое ожидание и дисперсию которой требуется оценить. Обозначим а1= 
, а2=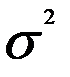 
и введем эти обозначения в выражение 
плотности вероятностей нормального распределения
= 
= 
:
; 
.
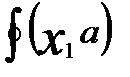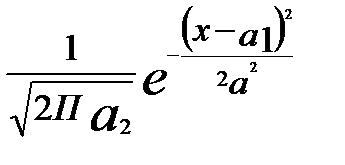Полученная с помощью некоторой выборочной функции = 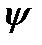(х1, х2, …, хп) конкретная оценка 
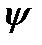= (х1, х2, …, хп) параметра «а» не дает, однако, возможности судить о том, как точно найденная оценка воспроизводит истинное значение параметра «а», даже если она является несмещенной и эффективной. Разумеется, величину разности 
нельзя определить точно, если распределение Х и величина 
не известны, так как 
есть всего лишь реализация случайной величины 
. Однако можно найти некоторую область, которая с вероятностью Р содержит истинное значение параметра «а». Если, например, F(Х) – функция распределения величины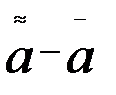 
, то можно рассчитать вероятность
Р = Р 
Если 
задано, то Р определяет вероятность того, что случайная переменная отличается от 
менее чем на 
, или вероятность того, что истинное значение параметра менее чем на отличается от оценки .
Истинное значение с вероятностью Р, задаваемой выражением Р = 
, находится между - и + , то есть в интервале 
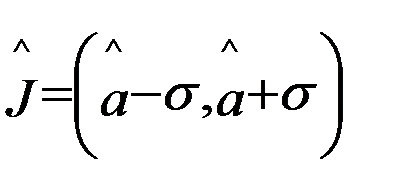, представляющем собой реализацию интервала
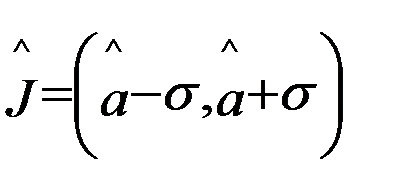
интервал 
называется обычно доверительным, а вероятность Р – доверительной вероятностью.
6. Если с 95%-ной надежностью, требуется обеспечить ошибку 
, возникает вопрос о том, какой минимальный объем выборки (n) для этого потребуется.
Задача здесь может быть поставлена так:
Найти минимальное целое число «n», для которого с вероятностью Р = 0,95 отклонение .
Для всякой заданной вероятности Р с помощью таблицы нормированного нормального распределения можно найти соответствующее значение 
.
При Р/2=0,95/2=0,475 находим Е = 1,96.
С учетом этого 
: При известной 
Таким образом, для достижения требуемой точности здесь потребуется сделать около 100 опытов.
Тема 3.