Оценка точности технологического процесса по производству изделий может быть осуществлена на основе сопоставления параметров эмпирического распределения, соответствующего рассматриваемому процессу, с заданным допуском на конкретный параметр изделия.
Оценим точность изготовления валиков диаметром ф 12 - 0,07(ф 12 h 10), обработанных на токарном станке. Для этого из большой партии возьмем выборку объемом N = 200 шт. Измерим диаметры валиков на приборе с ценой деления шкалы 0,01 мм. Считаем, что точность отсчета равна 0,005, т.е. половине цены деления шкалы. Измерения диаметров валиков необходимо выполнять в одном сечении (расположенном на определенном расстоянии от торца детали), соблюдая постоянство условий измерения. Расположив полученные действительные размеры di в порядке возрастания их значения, получим ряд случайных дискретных величин. Разность между наибольшим и наименьшим размерами валиков определит значения размаха “R” действительных размеров. R = dmax– dmin= 12,005 – 11,915 = 0,09 мм. (табл.).
Для упрощения расчетов разность dmax– dmin при N>50 разбивают на “K” интервалов. Рекомендуется применять К = 8…15. Для рассматриваемого примера К = 9.
Подсчитывают число деталей, имеющих размеры, ограниченные пределами каждого интервала: m1, m2,…, mК.
Случайными величинами считают размеры хi, равные среднему арифметическому из диаметров каждого интервала.
Среднее арифметическое значение действительных размеров может быть определено по формуле:
| № | Интервалы действительных размеров di, мм | Среднее значение интервала, мм | Число mi деталей в интервале | ti = xi - x | U = | mi u | miu2 |
| 11,915 – 11,925 | 11,920 | - 0,04 | - 4 | - 8 | |||
| 11,925 – 11,935 | 11,930 | - 0,03 | - 3 | - 18 | |||
| 11,935 – 11,945 | 11,940 | - 0,02 | - 2 | - 40 | |||
| 11,945 – 11,955 | 11,950 | - 0,01 | - 1 | - 48 | |||
| 11,955 – 11,965 | 11,960 | ||||||
| 11,965 – 11,975 | 11,970 | 0,01 | |||||
| 11,975 – 11,985 | 11,980 | 0,02 | |||||
| 11,985 – 11,995 | 11,990 | 0,03 | |||||
| 11,995 – 12,005 | 12,00 | 0,04 | |||||
| Итого | – | – |
|
|
При группировке данных по интервалам (табл.), среднее арифметическое значение действительных размеров определяется по следующей формуле:
где х0 – середина интервала с наибольшей частотой, мм.
∆ - широта интервала, мм.
х = 11,96 + 0,01 · 8/200 ≈ 11,96 мм.
Сумма квадратов отклонений может быть определена по формуле:
Среднее квадратическое отклонение равно:
Размерность S совпадает с размерностью случайной величины, для которой они определены. Чем меньше значение S, тем выше точность изготовления, т.е. меньше случайные погрешности изготовления.
Характер рассеяния значений случайной величины, которой в рассматриваемом примере является действительный размер валика представляется в виде гистограммы, приведенной на рис.
Параметры х, S и S2, определенные по данным выборки, дают лишь приближенную характеристику теоретического распределения. Между математическим ожиданием М (х), средним квадратическим отклонением σх, дисперсией D (x) и их эмпирическими аналогами х,S и S2 необходимо проводить четкое разграничение: первые следует рассматривать как постоянные, но неизвестные величины, характеризующие теоретическое распределение (генеральную совокупность), а вторые как случайные величины, которые будучи определенными из выборочных наблюдений, дают лишь
|
|
приближенную оценку М (х), σХ и D (x). Чем больше объем выборки, тем меньше разница между М (х) и х, σХ и S, D (x) и S2.
По результатам выборок и их объему можно установить границы, внутри которых с определенной, заданной из эксплуатационных требований, вероятностью будут находится значения М (х), σХ и D (x), характеризующие результаты многократных измерений. Эти границы определяют так называемый доверительный интервал. Соответствующую этому интервалу заданную вероятность называют надежностью или доверительной вероятностью “β”.
При законе нормального распределения (когда N> 30) доверительные интервалы, например, для М (х) с вероятностью β = 0,9973 определяются границами х ± 3 σХ, где σХ – среднее квадратическое отклонение для распределения средних арифметических величин х, определенное по формуле σХ = Si / √ N – 1.
Следовательно, границы доверительного интервала х =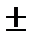 
3Si / √ N – 1.
В общем случае при большом объеме выборки и различной вероятности β доверительные интервалы для М (х) определяют по формуле:
x – z σХ<M (x) <x + z σХ.
Обычно задаются доверительной вероятностью β, равной 0,90; 0,95; 0,99 или 0,999, что соответствует значениям z = 1,645; 1,960; 2,576 и 3,291.
Пример. Считаем распределение погрешностей изготовления валиков при N= 200 (табл.) нормальным. Тогда σХ = Si / √ N – 1 = 0,015 / √ 199=0,001 мм.
При β = 0,90 доверительный интервал для М (х) составит: 11,96 – 1,645·0,001 < М (х) < 11,96 + 1,645·0,001, т.е. 11,958 < М (х) < 11,962.
Из рис следует, что часть деталей имеют размеры, выходящие за пределы допуска. Найдем относительное число А валиков, размеры которых могут иметь погрешности, выходящие за пределы допуска, т.е.число бракованных валиков. Выразив допуск в долях σ (приняв σ = 3), получим 0,07/0,015= 4,66. Примем z1 = - 2,33, z2 = 2,33.
|
|
Пользуясь таблицей нормального распределения получим ф0 (2,33) = 0,4901. Так как ф0 (- 2,33) = - ф0 (2,33), получим:
А = 100 - [ф0 (2,33) – ф0 (- 2,33)] 100 = 100 – 2 · 0,4901 · 100 = 1,98 %
При изготовлении валиков имелось смешение центра настройки
Е = х – с = - 0,005 (с – значение середины поля допуска, принимаемое за центр настройки).
С учетом смещения центра настройки (систематической погрешности) число бракованных деталей будет несколько большим.
Статистическое управление технологическим процессом и корректирование его параметров осуществляют путем предупредительного выборочного контроля изготовляемой продукции с целью обеспечения требуемого качества и предупреждения брака. При этом систематически дополняют контрольные карты, которые позволяют в любой момент времени оценить состояние технологического процесса, определяющий тот или иной параметр качества продукции, а в случае выхода его за границы регулирования – осуществить корректирование этого процесса.
Основным преимуществом статистического управления качеством перед сплошным контролем является то, что статистические методы позволяют обнаружить дефектные изделия не только, когда на их изготовление уже затрачены материальные средства и время, но когда изделия находятся еще в процессе производства и еще есть время его скорректировать.
Статистические методы управления в большей степени поддаются механизации с помощью средств вычислительной техники, чем сплошной контроль.
Эти методы позволяют при малых затратах средств обеспечивать не только точность технологического процесса в пределах заданного технологического допуска, но и создавать технологический запас точности.
Технологическим называют допуск, значения которого определяют с учетом экономически достижимой точности изготовления при выбранном технологическом процессе.
Технологический допуск определяется в виде:
Т2 = ωlim + Σ ∆i сист. (а)
где ωlim – практически предельное поле рассеяния контролируемого параметра,
Σ ∆i сист. – алгебраическая сумма неустранимых систематических погрешностей при данном технологическом процессе.
Формула (а) применима для определения технологического допуска только при непрерывном и надежном регулировании точности изготовления и контроле большой выборки деталей.
Другой метод определения технологического допуска основан на оценке рассеяния размеров по установочной (случайной) выборке – статистические характеристики в генеральной совокупности могут быть другими.
Технологический допуск должен быть таким, чтобы наименьшее и наибольшее значения действительных размеров деталей в генеральной совокупности не выходили за границы нижнего хmin = x – l·s и верхнего
хmax = x + l·s размеров, где х и s определяют по данным выборки,
l – коэффициент (табл), зависящий от объема выборки, допускаемой вероятности получения брака 2 β (или требуемой вероятности получения годных деталей (1 – 2 β)) и вероятности Р того, что (1 – 2 β) · 100 % деталей генеральной совокупности имеют размеры, лежащие в пределах назначенного допуска.
Тогда Т2=[(х + ls) – (x – ls)]+Σ ∆i сист.
Для технологического процесса, указанного по формуле (а)
Т2 = 6 · 0,015 + 0,005 = 0,095 мм. По формуле (б) Т2=[(11,96+3,47·0,015)-(11,96-3,47·0,015)]=0,109 мм.
Здесь значение Σ ∆i сист. принято равным смещению центра настройки “E”.
Таким образом, в рассматриваемом примере необходимо увеличить допуск квалитета 10 до допуска квалитета 11 (h11) или же применить более точный технологический процесс изготовления деталей.
Целесообразно создавать технологический запас точности, который можно характеризовать коэффициентом
Кт·т = ТF / Тч
Технологическим запасом точности называют положительную разность между функциональным допуском ТF параметра и технологическим допуском Тч , который обеспечивается при выбранном технологическом процессе. Для функциональных размеров ответственных деталей коэффициент Кт·т не должен быть меньше 1,2. В этом случае создается дополнительный ресурс точности, обеспечивающий более длительное сохранение заданной точности изделия в процессе его эксплуатации и повышенную его долговечность, а также запас точности настройки станка.
В процессе производства можно управлять качеством машин, их составных частей и деталей статистическими методами и обеспечивать заданное значение Кт·т. Статистическое управление качеством, выполненное с помощью контрольных карт, заключается в своевременном установлении возможности появления брака по ограниченному числу наблюдений (выборок) и немедленном принятии мер по обеспечению требуемого качества изделий.
Применяют несколько методов управления: метод средних арифметических, метод размахов, метод медиан, метод средних квадратических отклонений и др.
Внедрение статистического управления точностью технологических процессов дает большой экономический эффект в результате сокращения потерь от брака, повышения точности и долговечности изделий, более рационального использования оборудования и материалов.
4.Контрольные карты для качественных признаков. Способы наглядного представления качества процесса.
Существуют следующие виды контрольных карт:
- средних арифметических значений (х – карта).
- медиан (х – карта)
- средних квадратических отклонений (S – карта)
- размахов (R – карта)
- числа дефектных единиц продукции (nP – карта)
- доли дефектных единиц продукции (P – карта)
- числа дефектов (с – карта)
- числа дефектов на единицу продукции (U – карта)
Первые четыре вида контрольных карт применяют при контроле по количественному признаку, последние четыре – при контроле по альтернативному признаку.
Контрольную карту х – R рекомендуется применять для процессов с высокими требованиями к точности, для продукции, связанных с обеспечением безопасности потребителя, для управления процессами и т.д.
Контрольная карта Р применяется для контроля и регулирования технологического процесса на основе использования доли дефектных изделий, полученной делением числа обнаруженных дефектных изделий на число проверенных изделий. Контрольная карта nP применяется для контроля в случаях, когда контрольным параметром является число дефектных изделий при постоянном объеме выборки “n”. Эта контрольная карта соответствует контрольной карте “P” с вариантом постоянного “n” и по существу одинакова с ней.
Статистический контроль большей частью производится непосредственно в ходе технологического процесса, предохраняя производство от возникновения брака, давая возможность правильной наладки и своевременного регулирования производственных операций.
Состояние производственного процесса отражается на контрольном графике, на который в виде точек в определенном масштабе наносятся действительные размеры проверенных деталей.
Для заполнения графиков берутся пробы. Пробой называют несколько деталей, взятых для измерения или испытания непосредственно после их изготовления. Пробы должны браться через равные промежутки времени. В каждой пробе должно быть одинаковое количество деталей. Результаты измерения по каждой детали, входящей в пробу, отмечается на графике отдельной точкой.
1 – верхний предел чертежного допуска
2 – нижний предел чертежного допуска
Б1 – верхняя граница крайних значений в пробах
Б2 – нижняя граница крайних значений в пробах
А1 – верхняя граница для средних арифметических
А2 – нижняя граница для средних арифметических
На контрольном графике наносятся две внешние границы (Б1, Б2) и две внутренние (А1, А2).
Крайние точки пробы не должны переходить за внешние границы Б1 и Б2, средние арифметические должны располагаться между внутренними границами А1 и А2. Контрольные границы не являются произвольными, они определяются расчетным путем. При этом внешние границы всегда должны получаться более узкими, чем границы поля допуска, с тем чтобы исключить возможность выхода обрабатываемых деталей за пределы поля допуска.
Расчет контрольных границ будет различным для кривых разного типа. При получении распределения по кривой Гаусса перед расчетом контрольных границ необходимо вычислить основные статистические характеристики: математическое ожидание и среднее квадратическое отклонение.
Процесс установления соответствия распределения результатов измерений нормальному закону, рассмотрим на основе данных, приведенных в табл. и гистограммы, соответствующий этим данным (рис).
1. Среднее арифметическое значение результатов измерения (х) определяется по формуле:
Х = ∆ + х0 = 0,01 + 40,045 ≈ 40,045 мм.
где Ui =; х0 – середина интервала с наибольшей частотой
хi – середина “ i ” – го интервала.
Значения Ui и miUi, соответствующие каждому интервалу приведены в табл.2.
2. Определяем дисперсию μ (х) по формуле:
3. Среднее квадратическое отклонение равно:
S = √ μ (х) = √ 1,635 · 10 – 4 = 1,28 / 100 = 0,0128 мм.
4. Соответствие эмпирического распределения предполагаемому теоретическому распределению устанавливают с помощью критерия λ2 – критерия Пирсона. При этом параметры х, S и μ (х). определенные по результатам выборки применяются в качестве характеристик теоретического распределения: математического ожидания М (х), среднего квадратического отклонения σх и дисперсии D (х).
6. Приняв значение статистической надежности
Р = 1 – α = 0,9 и α / 2 = 0,05 определим значения
λ20,95; 9 = 16,919 и λ20,05; 9 = 3,325.
3,325 < 6,113 < 16,919
Это свидетельствует о том, что рассматриваемые результаты измерений и, соответствующая гистограмма может быть представлена нормальным законом распределения.
7. При получении распределения по нормальному закону внутренние контрольные границы А1 и А2 подсчитываются:
- для метода средних арифметических по формулам:
где n – число деталей в пробе.
- для метода медиан по формулам:
Внешние контрольные границы Б1 и Б2 подсчитываются по формулам:
Б1 = х + 2,5 σ; Б2 = х – 2,5 σ.
Чертежное поле допуска составляет х ± 3σ.
По данным рассмотренного примера:
Б1 = х + 2,5 σ = 40,045 + 2,5 · 0,0128 = 40,077 мм. Б2 = 40,013 мм.
Чертежные поля допуска:
Е1 = х + 3 · σ = 40,045 + 3 · 0.0128 = 40,083 мм.
Е2 = х – 3 · σ = 40,045 – 3 · 0.0128 = 40,007 мм.
Контрольная карта позволяет не только обнаруживать разладку процесса, но и помогает выяснить причины возникновения разладки.
Кроме того, она служит документом, который может быть использован для принятия обоснованных решений по улучшению качества продукции.
Тема 7.