Исходные данные для корреляционно-регрессионного анализа представлены в таблице 3.1.
Таблица 3.1
Данные о среднегодовой численности занятых в экономике и основных фондах по полной учетной стоимости на конец 2015г. по Центральному и Северо-Западному ФО
| № п/п | Среднегодовая численность занятых в экономике, тыс. человек (y) | Основные фонды в экономике (по полной учетной стоимости на конец года), млн. руб. (x) |
| 698,1 | ||
| 522,2 | ||
| 693,2 | ||
| 1051,7 | ||
| 481,5 | ||
| 487,5 | ||
| 296,2 | ||
| 491,9 | ||
| 482,2 | ||
| 500,2 | ||
| 570,3 | ||
| 742,9 | ||
| 622,3 | ||
| 289,6 | ||
| 425,3 | ||
| 589,1 | ||
| 571,9 | ||
| 473,9 | ||
| 743,2 | ||
| 397,8 | ||
| 303,4 | ||
| 318,3 |
На рисунке 3.1 представлено корреляционное поле зависимости среднегодовой численности занятых в экономике (y) от стоимости основных фондов в экономике (х).
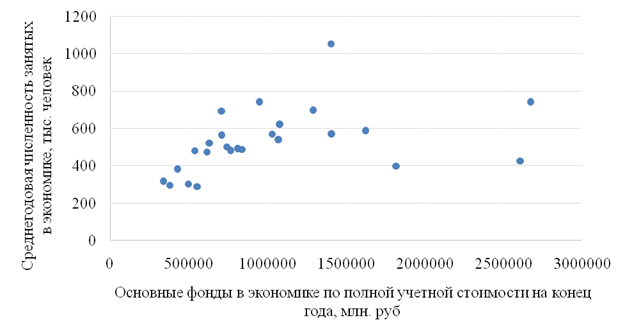
Рисунок 3.1 Поле корреляции
Исходя из характера расположения точек поля корреляции можно сделать вывод о наличии прямой связи между признаками х и у.
Эмпирический коэффициент детерминации  характеризует долю факторной дисперсиив общей дисперсии результативного признака и рассчитывается по формуле:
характеризует долю факторной дисперсиив общей дисперсии результативного признака и рассчитывается по формуле:

где 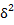 - межгрупповая дисперсия, характеризующая систематическую вариацию результативного признака под влиянием признака-фактора, положенного в основание группировки;
- межгрупповая дисперсия, характеризующая систематическую вариацию результативного признака под влиянием признака-фактора, положенного в основание группировки;
 - общая дисперсия результативного признака, измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.
- общая дисперсия результативного признака, измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.
Для расчета общей дисперсии 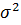 по несгруппированным данным строится таблица 3.2.
по несгруппированным данным строится таблица 3.2.
Таблица 3.2
Расчёт общей дисперсиисреднегодовой численности занятых в экономике(у – результативный признак)
| № п/п | Среднегодовая численность занятых в экономике, тыс. человек (yi) | 
| 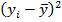
|
| 698,1 | 168,4 | 28358,56 | |
| 522,2 | -7,5 | 56,25 | |
| 693,2 | 163,5 | 26732,25 | |
| 1051,7 | 522,0 | 272484,00 | |
| 481,5 | -48,2 | 2323,24 | |
| 487,5 | -42,2 | 1780,84 | |
| 296,2 | -233,5 | 54522,25 | |
| 35,3 | 1246,09 | ||
| 11,3 | 127,69 | ||
| -146,7 | 21520,89 | ||
| 491,9 | -37,8 | 1428,84 | |
| 482,2 | -47,5 | 2256,25 | |
| 500,2 | -29,5 | 870,25 | |
| 570,3 | 40,6 | 1648,36 | |
| 742,9 | 213,2 | 45454,24 | |
| 622,3 | 92,6 | 8574,76 | |
| 289,6 | -240,1 | 57648,01 | |
| 425,3 | -104,4 | 10899,36 | |
| 589,1 | 59,4 | 3528,36 | |
| 571,9 | 42,2 | 1780,84 | |
| 473,9 | -55,8 | 3113,64 | |
| 743,2 | 213,5 | 45582,25 | |
| 397,8 | -131,9 | 17397,61 | |
| 303,4 | -226,3 | 51211,69 | |
| 318,3 | -211,4 | 44689,96 | |
| Итого | 13241,7 | X | 705236,48 |
| Средняя | 529,7 | X | 28 209,5 |
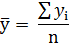

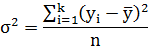
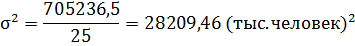
Для расчета межгрупповой дисперсии использована таблица 3.3:
Таблица 3.3
Расчёт межгрупповой дисперсии среднегодовой численности занятых в экономике (у - результативный признак)
| № п/п | Группы субъектов РФ по размеру основных фондов в экономике (по полной учетной стоимости на конец года), млн. руб. | Число субъектов РФ | В среднем на один субъект РФ среднегодовой численности занятых в экономике, тыс. человек | 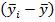
| 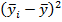
| 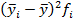
|
| 337 713 – 921 013 | 449,2 | -80,5 | 6 480,25 | 90 723,5 | ||
| 921 013 – 1 504 313 | 685,5 | 155,8 | 24 273,64 | 169 915,5 | ||
| 1 504 313 – 2 087 613 | 493,5 | -36,2 | 1 310,44 | 2 620,88 | ||
| 2 087 613 – 2 670 913 | 584,3 | 54,6 | 2 981,16 | 5 962,32 | ||
| Итого: | Х | Х | 269 222,2 |

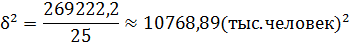
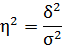

Эмпирическое корреляционное отношение  характеризует тесноту связи между признаками и рассчитывается по формуле:
характеризует тесноту связи между признаками и рассчитывается по формуле:
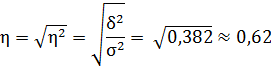
Эмпирическое корреляционное отношение 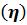 изменяется в пределах от 0 до 1 и характеризует степень влияния группировочного признака (основных фондов в экономике по полной учетной стоимости на конец года) на вариацию результативного признака (среднегодовой численности занятых в экономике).
изменяется в пределах от 0 до 1 и характеризует степень влияния группировочного признака (основных фондов в экономике по полной учетной стоимости на конец года) на вариацию результативного признака (среднегодовой численности занятых в экономике).
Для классификации связи используется шкала Чеддока, согласно которой характеристика связи в данном случае заметная.
Для оценки тесноты предполагаемой линейной связи линейный коэффициент корреляции Пирсона ( можно рассчитать по формуле:
можно рассчитать по формуле:
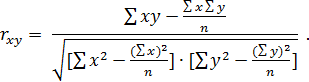
Для удобства вычислений составляется расчетная таблица 3.4:
Таблица 3.4
Расчет линейного коэффициента корреляции и параметров линейного уравнения регрессии
| № п/п | Основные фонды в экономике (по полной учетной стоимости на конец года), млн. руб. (xi) | Среднегодовая численность занятых в экономике, тыс. человек (yi) | 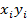
| 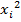
| 
|
| 698,1 | 900351437,7 | 487343,6 | |||
| 522,2 | 327626191,2 | 272692,8 | |||
| 693,2 | 488800275,2 | 480526,2 | |||
| 1051,7 | 1106072,9 | ||||
| 481,5 | 258439828,5 | 231842,3 | |||
| 487,5 | 237656,3 | ||||
| 296,2 | 87734,4 | ||||
| 319225,0 | |||||
| 292681,0 | |||||
| 146689,0 | |||||
| 491,9 | 397246142,5 | 241965,6 | |||
| 482,2 | 368613450,2 | 232516,8 | |||
| 500,2 | 369809864,8 | 250200,0 | |||
| 570,3 | 587045718,9 | 325242,1 | |||
| 742,9 | 703274456,9 | 551900,4 | |||
| 622,3 | 669460383,2 | 387257,3 | |||
| 289,6 | 159290425,6 | 83868,2 | |||
| 425,3 | 180880,1 | ||||
| 589,1 | 955147888,8 | 347038,8 | |||
| 571,9 | 802824641,5 | 327069,6 | |||
| 473,9 | 290660878,2 | 224581,2 | |||
| 743,2 |  7132926928516 7132926928516
| 552346,2 | |||
| 397,8 | 721942954,2 | 158244,8 | |||
| 303,4 | 150021591,2 | 92051,6 | |||
| 318,3 | 107494047,9 | 101314,9 | |||
| Итого: | 13241,7 | 14483399105,2 | 35209865567676,0 | 7718941,2 |
По данным таблицы 2.3.4 рассчитаем линейный коэффициент парной корреляции:
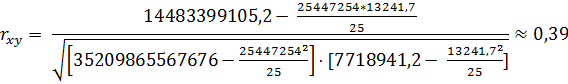
Линейное уравнение связи имеет вид 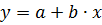 .
.
В линейном уравнении парной регрессии:
· параметр а показывает усреднённое влияние на результативный признак неучтённых факторов, может не иметь экономической интерпретации;
· параметр b называется коэффициентом регрессии и показывает, на сколько единиц в среднем изменится значение результативного признака при увеличении факторного на единицу.
Для нахождения его параметров методом наименьших квадратов можно воспользоваться формулами:
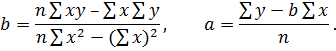
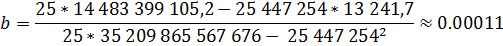
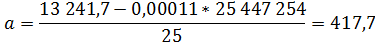
Таким образом, линейное уравнение парной регрессии имеет вид:
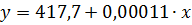
Для удобства, график построенной зависимости представлен на рисунке 2.3.2 в той же системе координат, что и поле корреляции.

Рисунок 3.2 Линейное уравнение парной регрессии на поле корреляции
Вывод:Значение линейного коэффициента корреляции находится в границах 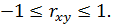 Т. к в данном случае
Т. к в данном случае 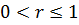 , то связь прямая.
, то связь прямая.
Чем ближе абсолютное значение 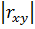 к 1, тем теснее линейная связь, и тем лучше линейная зависимость согласуется с данными наблюдений. Для классификации связи по значению линейного коэффициента корреляции используется шкала Чеддока. Т.к.
к 1, тем теснее линейная связь, и тем лучше линейная зависимость согласуется с данными наблюдений. Для классификации связи по значению линейного коэффициента корреляции используется шкала Чеддока. Т.к.  , то по шкале Чеддока связь междуразмеромсреднегодовойчисленностизанятыхвэкономикеиосновнымифондамивэкономикепополнойучетнойстоимостинаконецгодаумеренная.
, то по шкале Чеддока связь междуразмеромсреднегодовойчисленностизанятыхвэкономикеиосновнымифондамивэкономикепополнойучетнойстоимостинаконецгодаумеренная.