Вариант №
Тема:……………………………………………………………………………………………………………………………………………………………………………
Выполнил: студент гр. Епанчинцев Сергей
Проверил профессор: Корщиков В.Д.
Г. Екатеринбург 2002 г.
РАСТЯЖЕНИЕ (СЖАТИЕ) ПРЯМОГО БРУСА - ЗАДАНИЕ №1
Деформация центрального растяжения (сжатая) обусловлена возникновением в любом поперечном сечении деформируемого стержня одного внутреннего усилия – ПРОДОЛЬНОЙ СИЛЫN. Она -равна алгебраической сумме проекций внешних сил на ось стержня (ось Z) действующих на оставленную часть бруса (слева или справа от рассматриваемого сечения).
Максимальные нормальные напряжения действуют в поперечном сечении, распределены равномерно по сечению и равны:

где N – продольная сила, Н;
F – площадь поперечного сечения, мм2
Единица измерения напряжения – МЕГАПАСКАЛЬ – МПа, IМПа=IН/мм2
Прочность деформируемого элемента конструкций обеспечивается, если
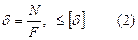
где  - допускаемое напряжение для материала стержня.
- допускаемое напряжение для материала стержня.
Оно равно  (пластичные материалы)
(пластичные материалы)
Или  (хрупкие материалы)
(хрупкие материалы) 
Здесь  и
и  - соответственно предел текучести и предел прочности материала;
- соответственно предел текучести и предел прочности материала;
К – требуемый коэффициент запаса прочности.
Относительная (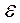 ) или абсолютная (
) или абсолютная ( ) продольная деформация определяется по закону Гука
) продольная деформация определяется по закону Гука
 и
и 
где Е – модуль продольной упругости, величина постоянная для каждого материала, для сталей Е=2*105 МПа.
l- длина стержня, мм.
Поперечная относительная деформация равна

где  - коэффициент поперечной деформации (коэф. Пуассона), для сталей
- коэффициент поперечной деформации (коэф. Пуассона), для сталей  .
.
Примеры решения задач.
Задача №1
 Для заданного ступенчатого стержня (рис.1.) построить эпюры продольных сил и нормальных напряжений, определить перемещения сечения АА, если Р1=50 кН; Р2=150 кН; Р3=30 кН; а=0,4 м; F=2,5 см2.
Для заданного ступенчатого стержня (рис.1.) построить эпюры продольных сил и нормальных напряжений, определить перемещения сечения АА, если Р1=50 кН; Р2=150 кН; Р3=30 кН; а=0,4 м; F=2,5 см2.
Рис. 1.
Решение
1. Разбиваем стержень на участки 1,2,3,4, границами которых являются сечения, где приложены внешние силы и меняются размеры сечения.
2. Применяя метод сечения, определяем продольные силы по участкам. Построение эпюры ведём справа, со свободного конца. Проведя произвольное сечение на 1 участке и рассматривая условие равновесия правой оставленной части, можем записать (см.рис.2а)


Поступая аналогично для второго участка, будем иметь (см.рис.2б)

Рис.2
Продольные силы и нормальные напряжения, направленные от сечения и вызывающие деформацию растяжения будем считать положительными, направленными к сечению и вызывающим деформацию сжатия – отрицательными.
Эпюра продольных сил N представлена на рис. 1а. В сечениях, где приложены внешние силы, получили скачки, равные этим словам.
3. Зная величину продольной силы на каждом участке и используя формулу (1), определяем нормальные напряжения, действующие в поперечных сечениях (рис. 1б):

4. Перемещение сечения А-А определяется деформацией части стержня, расположенного между неподвижным сечением (заделкой) и рассматриваемым сечением А-А.

Сечение А-А переместиться влево на 1,65 мм.
Задача №2
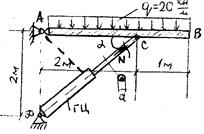 Определить диаметр d штока гидроцилиндра ГЦ, поддерживающего жесткую плиту АВ стенда для мойки тракторов (рис.3.) если он изготовлен из стали 45, имеющей
Определить диаметр d штока гидроцилиндра ГЦ, поддерживающего жесткую плиту АВ стенда для мойки тракторов (рис.3.) если он изготовлен из стали 45, имеющей 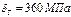 , а необходимый запас по прочности К=3.
, а необходимый запас по прочности К=3.
Рис.3.
Решение.
- Делаем сечение, обозначаем усилие в штоке при N. Из условия равновесия системы определяем усилие в штоке. Он испытывает деформацию сжатия.
-

- Применив условие прочности (2) при растяжении (сжатии) определяем диаметр штока

Округляем до ГОСТовских значений d=30мм.
Задача №3

Для заданного стального ступенчатого стержня, защемлённого с обеих сторон (рис 4.), построить эпюр продольных сил и определить максимальное нормальное напряжение в опасном сечении, если
Р=300кН; а=0,25 м; F=2 см2, Е=2*105 МПа.
Определить также величину полной потенциальной энергии деформации.
Рис.4.
Решение
- Обозначим опорные реакции Ra и Rb и составив уравнение равновесия системы в виде

-Ra+P-Rb=0 Ra+Rb=P (1)
видим, что реакции определить не можем. Не зная реакции, мы не сможем определить с помощью метода сечений внутренние усилия- продольные силы. Следовательно, заданная система является статически неопределимой. Для её расчёта необходимо составить дополнительное уравнение перемещений. Превращаем заданную систему в статически определимую, отбросив одну из опор, например опору В (см. рис 4а). действие опоры В заменяем реакцией Rв. Отбросив опору В, мы дали возможность сечению В под действием сил Р и Rв перемещаться, но в заданной системе сечение В не имеет перемещений (жёсткая заделка).
Отразив этот факт, мы получаем необходимое уравнение перемещения

Используя закон Гука, можем записать (см. рис. 4б.в.)

Поставив значения перемещения (3) в уравнение (2), и решив его, получим

Тогда из (1) RA=P-RB =300-100=200кН.
- Строим эпюры продольных сил по участкам (см. рис. 5)

 Нормальные напряжения в поперечных сечениях равны
Нормальные напряжения в поперечных сечениях равны
Рис.5.

- Полная потенциальная энергия деформации стержня равна сумме энергий, накапливаемых на каждом участке

Задача №4
 Жесткая плита АВ поддерживается двумя стальными стержнями одинакового сечения (рис.6.)
Жесткая плита АВ поддерживается двумя стальными стержнями одинакового сечения (рис.6.)
Определить, какие возникнут температурные напряжения в обоих стержнях, если будет нагреваться только 1 стержень на 800. Коэф. температурного расширения стали а=12*10-6, Е=2*105 МПа.
Рис.6.
Решение.
- Вследствие нагрева 1 стержень, стремясь расширится (удлиниться) будет воздействовать на второй стержень, вызывая в нём сжимающее усилие N2. Второй стержень, сопротивляясь, будет тоже воздействовать на 1 стержень, вызывая в нём сжимающее усилие N1. Для определения этих усилий составим уравнение равновесия системы в виде

Таким образом, имеем одно уравнение с 2-мя неизвестными усилиями. Следовательно, система является статически неопределимой. Для её расчёта составляем уравнение перемещений из следующих рассуждений (см. рис. 7): если бы в конструкции не было второго стержня, то 1 стержень за счёт нагрева получил бы температурное удлинение 
 В действительности же второй стержень, сопротивляясь, будет ограничивать температурное удлинение 1 стержня. Точка приложения усилия N1 получит перемещение
В действительности же второй стержень, сопротивляясь, будет ограничивать температурное удлинение 1 стержня. Точка приложения усилия N1 получит перемещение  , которое очевидно будет равно
, которое очевидно будет равно

Точка приложения усилия N2 получает перемещение 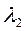 , которое, спроектировав на направление действия усилия N2 , можем выразить через его деформацию
, которое, спроектировав на направление действия усилия N2 , можем выразить через его деформацию 

Используя подобие прямоугольных треугольников с катетами  ,
, 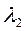 , 5 и 3 м, запишем
, 5 и 3 м, запишем

с учётом выражений (2) и (3) будем иметь

Из рис.6. видно, что 
Решая совместно уравнение (1) и (4), определяем усилия в стержнях

- Температурные нормальные напряжения, возникающие в стержнях будут равны

Задача №5
 Жёсткая плита АВ должна поддерживаться двумя стальными стержнями 1 и 2, у которых сечения равны F1=F; F2=0,8F (рис.8). При изготовлении 1 стержень оказался короче требуемой длины на величину
Жёсткая плита АВ должна поддерживаться двумя стальными стержнями 1 и 2, у которых сечения равны F1=F; F2=0,8F (рис.8). При изготовлении 1 стержень оказался короче требуемой длины на величину 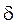 . Определить, какие монтажные напряжения возникнут в стержнях при сборке конструкции, если
. Определить, какие монтажные напряжения возникнут в стержнях при сборке конструкции, если
Рис.8.

Решение
- При сборке конструкции (рис. 8.) зазор
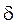 мы будем «закрывать» очевидно за счёт деформации растяжения 1 стержня -
мы будем «закрывать» очевидно за счёт деформации растяжения 1 стержня -  и перемещения
и перемещения 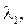 обусловленного деформацией сжатия стержня 2 (рис. 9). Составим уравнение равновесия системы в виде
обусловленного деформацией сжатия стержня 2 (рис. 9). Составим уравнение равновесия системы в виде 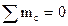
 =0, т.е. N1 = 0.866 N2 (1)
=0, т.е. N1 = 0.866 N2 (1)

Рис.9
Отсюда следует, что система статически неопределима. Дополнительное уравнение перемещений составим, рассматривая характер деформации конструкции (см.рис.9).
Очевидно, что  , но из подобия треугольников видим, что
, но из подобия треугольников видим, что
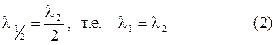
Перемещение 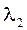 точки приложения усилия N2 выразим через деформацию укорочения стержня 2.
точки приложения усилия N2 выразим через деформацию укорочения стержня 2.

Таким образом, получим после преобразований

N2= 
С учётом выражения (1), усилие в 1 стержне составит
N1=0,866*0,204*10-3  = 0,176*10-3
= 0,176*10-3 
- Монтажные напряжения в стержнях очевидно будут равны

Варианты домашних заданий
В домашнее задание №1 входит решение 4 задач в соответствии с вариантом, выданным преподавателем. Номера задач по каждому варианту заданы в таблице 1. первая цифра №-задачи означает непосредственно сам номер задачи, которую надо решить, а вторая цифра – номер строки исходных данных.
Таблица №1
| Вариант | Номера задач | |||
| II | III | IV | ||
| 1-1 | 9-1 | 16-3 | 25-1 | |
| 1-2 | 9-2 | 17-1 | 25-2 | |
| 1-3 | 9-3 | 17-2 | 25-3 | |
| 1-4 | 9-4 | 17-3 | 25-4 | |
| 1-5 | 10-1 | 17-4 | 26-1 | |
| 2-1 | 10-2 | 18-1 | 26-2 | |
| 2-2 | 10-3 | 18-2 | 26-3 | |
| 2-3 | 10-4 | 18-3 | 26-4 | |
| 2-4 | 11-1 | 19-1 | 27-1 | |
| 3-1 | 11-2 | 19-2 | 27-2 | |
| 3-2 | 11-3 | 19-3 | 27-3 | |
| 3-3 | 11-4 | 19-4 | 27-4 | |
| 3-4 | 12-1 | 20-1 | 27-5 | |
| 4-1 | 12-2 | 20-2 | 28-1 | |
| 4-2 | 12-3 | 20-3 | 28-2 | |
| 4-3 | 12-4 | 20-4 | 28-3 | |
| 5-1 | 13-1 | 21-1 | 28-4 | |
| 5-2 | 13-2 | 21-2 | 28-5 | |
| 5-3 | 13-3 | 21-3 | 29-1 | |
| 6-1 | 13-4 | 21-4 | 29-2 | |
| 6-2 | 13-5 | 22-1 | 29-3 | |
| 6-3 | 14-1 | 22-2 | 29-4 | |
| 7-1 | 14-2 | 22-3 | 30-1 | |
| 7-2 | 14-3 | 23-1 | 30-2 | |
| 7-3 | 15-1 | 23-2 | 20-3 | |
| 7-4 | 15-2 | 23-3 | 30-4 | |
| 8-1 | 15-3 | 23-4 | 31-1 | |
| 8-2 | 15-4 | 24-1 | 31-2 | |
| 8-3 | 16-1 | 24-2 | 31-3 | |
| 8-4 | 16-2 | 24-3 | 31-4 |
Задача №1

В заданной схеме навески трактора (рис.9) определить усилия N, напряжения  и деформации
и деформации 
 в обоих стальных стержнях, если
в обоих стальных стержнях, если
| № | Р, кН | 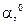
|  , м , м
| F1, мм2 | l2, м | F2, мм2 |
| 1-1 | 15,5 | 0,9 | 0,9 | |||
| 1-2 | 19,0 | 1,2 | 1,2 | |||
| 1-3 | 38,0 | 1,5 | 1,5 | |||
| 1-4 | 30,0 | 1,30 | 1,3 | |||
| 1-5 | 35,0 | 1,0 | 0,8 |
Рис.9
Задача №2
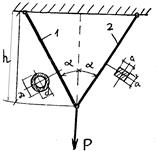 Какой груз Р можно приложить к данной подвеске, изготовленной из 2-х стержней (рис.10)
Какой груз Р можно приложить к данной подвеске, изготовленной из 2-х стержней (рис.10)
Стержень 1 – СТАЛЬНОЙ, трубчатого сечения, с допускаемым напряжением 

Стержень 2 – из прочного алюминиевого сплава, квадратного поперечного сечения со стороной «а», с допускаемым напряжением 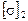
Рис.10
| № | 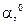
| 1-й стержень | 2-ой стержень | |||
| Д, мм | С=d/Д |  , МПа , МПа
| а, мм | 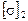 , МПа , МПа
| ||
| 2-1 | 0,80 | |||||
| 2-2 | 0,85 | |||||
| 2-3 | 0,90 | |||||
| 2-4 | 0,75 |
Задача №3
 Опорная жесткая плита АВ стенда для разборки тракторов ТИПА Т-150 К закреплена шарнирно в точке А и поддерживается силовым гидроцилиндром ГЦ (рис. 11). Определить диаметр d штока гидроцилиндра, изготовленного из стали, имеющей предел текучести
Опорная жесткая плита АВ стенда для разборки тракторов ТИПА Т-150 К закреплена шарнирно в точке А и поддерживается силовым гидроцилиндром ГЦ (рис. 11). Определить диаметр d штока гидроцилиндра, изготовленного из стали, имеющей предел текучести  . Конструкция должна иметь запас прочности «К» при давлении колёс трактора Р.
. Конструкция должна иметь запас прочности «К» при давлении колёс трактора Р.
| № | Р, кн | l, м |  , МПа , МПа
| К |
| 3-1 | 14,0 | 2,2 | ||
| 3-2 | 16,5 | 2,4 | 2,5 | |
| 3-3 | 18,0 | 2,5 | 1,5 | |
| 3-4 | 20,0 | 3,0 | 2,0 |
Рис.11
Задача №4
 Подобрать размеры поперечного сечения двух стальных тяг АВ и СД, поддерживающих две жесткие балки ЕД и СК (рис.12), если нагрузка на конструкцию равна Р, а допускаемое напряжение для материала тяг равно
Подобрать размеры поперечного сечения двух стальных тяг АВ и СД, поддерживающих две жесткие балки ЕД и СК (рис.12), если нагрузка на конструкцию равна Р, а допускаемое напряжение для материала тяг равно  .
.
| № | а, м | Р, кн |  , МПа , МПа
|
| 4-1 | 1,0 | ||
| 4-2 | 1,2 | ||
| 4-3 | 1,5 |
Рис. 12
Задача №5
 В заданной конструкции (рис.13) всё четыре стержня стальные, одинакового поперечного сечения, состоящего из 2-х разнобоких уголков. Определить напряжения, возникающие в стержнях при заданной нагрузке Р.
В заданной конструкции (рис.13) всё четыре стержня стальные, одинакового поперечного сечения, состоящего из 2-х разнобоких уголков. Определить напряжения, возникающие в стержнях при заданной нагрузке Р.
| № | Р, кН | № уголка | Размеры, м | |
| а | в | |||
| 5-1 | 50х50х3 | 3,0 | 4,0 | |
| 5-2 | 70х70х6 | 3,5 | ||
| 5-3 | 75х75х7 | 4,0 | 4,0 |
Рис. 13
Задача №6
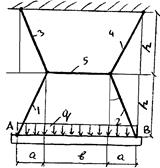
Схема сцепки бороны АВ с трактором приведена на рис. 14. определить напряжение во всех 5 тягах, изготовленных из круглого стального прутка диаметром d, если сопротивление почвы при бороновании составляет q.
| № | q, кН/м | a, м | b, м | h, м | d, мм |
| 6-1 | 1,0 | 0,5 | 2,0 | 0,75 | |
| 6-2 | 1,2 | 0,75 | 3,0 | 1,00 | |
| 6-3 | 1,5 | 0,6 | 4,0 | 1,4 |
Рис.14
Задача №7

Подобрать размеры сечения двух растяжек 1 и 2, заданной конструкции трубчатое сечение при допускаемом напряжении материала  , если нагрузка равна Р (рис. 15)
, если нагрузка равна Р (рис. 15)
| № | Р, кН | А, м | h,м |  , МПа , МПа
| С=d/Д |
| 7-1 | 0,8 | 0,6 | 0,7 | ||
| 7-2 | 0,5 | 0,8 | 0,8 | ||
| 7-3 | 0,4 | 0,5 | 0,85 | ||
| 7-4 | 0,6 | 1,0 | 0,75 |
Рис.15
 Задача №8
Задача №8
Определить напряжения в стальных тягах 1 и 2 заданной конструкции, нагруженной силой Р (рис.16). определить также вертикальное перемещение точки приложения внешней силы (точки К), если:
| № | Р, кН | а, м | № уголка | h,м | № швеллера | 
|
| 8-1 | 1,0 | 80х80х8 | 1,5 | |||
| 8-2 | 1,2 | 90х90х6 | 1,5 | |||
| 8-3 | 1,5 | 100х100х7 | 2,0 | |||
| 8-4 | 2,0 | 100х100х10 | 2,2 |
Рис.16
Задача №9
 Для заданного ступенчатого бруса с жёстко заделанными концами и нагруженного силами Р1 и Р2 построить эпюру продольных сил, определить максимальное напряжение в опасном сечении и подсчитать полную потенциальную энергию деформации (рис.17)
Для заданного ступенчатого бруса с жёстко заделанными концами и нагруженного силами Р1 и Р2 построить эпюру продольных сил, определить максимальное напряжение в опасном сечении и подсчитать полную потенциальную энергию деформации (рис.17)
| № | Р1, кН | Р2, кН | F, см2 | а,м | Е, МПа |
| 9-1 | 10,0 | 0,4 | 2,0*105 | ||
| 9-2 | 13,0 | 0,5 | 1,0*105 | ||
| 9-3 | 15,0 | 0,7 | 1,2*105 | ||
| 9-4 | 20,0 | 0,6 | 2,0*105 |
Рис. 17
Задача №10

Стержень, состоящий из 2-х разнородных материалов, защемлён с обоих концов и нагружён силой Р (рис. 18). Определить напряжения в каждой части стержня, если:
| № | Р, кН | l1, м | Е, МПа | l2, м | Е2, МПа | F, см2 |
| 10-1 | 0,8 | 1*105 | 0,2 | 0,7*105 | 10,0 | |
| 10-2 | 0,6 | 1,2*105 | 0,4 | 1,0*105 | 15,0 | |
| 10-3 | 0,8 | 0,7*105 | 0,5 | 1,2*105 | 20,0 | |
| 10-4 | 1,2 | 2,0*105 | 0,8 | 0,7*105 | 25,0 |
Рис.18
Задача №11
 Жёсткая плита АВ загрузочного устройства шарнирно закреплена в точке В и поддерживается двумя стальными стойками 1 и 2 (рис.19). Определить усилия и напряжения в этих стержнях при заданной нагрузке, если:
Жёсткая плита АВ загрузочного устройства шарнирно закреплена в точке В и поддерживается двумя стальными стойками 1 и 2 (рис.19). Определить усилия и напряжения в этих стержнях при заданной нагрузке, если:
| № | q, кН/м | a, м | l1, м | F1, см2 | l2, м | F2, см2 |
| 11-1 | 2,5 | 1,2 | 10,0 | 0,8 | 8,0 | |
| 11-2 | 2,0 | 1,5 | 12,5 | 1,0 | 10,0 | |
| 11-3 | 1,5 | 1,6 | 14,0 | 1,2 | 12,0 | |
| 11-4 | 1,0 | 1,8 | 19,0 | 1,5 | 14,5 |
Рис.19
Задача №12
 Жёсткая плита АВ стенда для мойки тракторов (рис.20) поддерживается шарниром «С» и двумя стальными стержнями 1 и 2. Определить с каким запасом прочности будет работать заданная конструкция, если:
Жёсткая плита АВ стенда для мойки тракторов (рис.20) поддерживается шарниром «С» и двумя стальными стержнями 1 и 2. Определить с каким запасом прочности будет работать заданная конструкция, если:
Рис.20
| № | Р, кН | a, м | l1, м | l2, м |  , МПа , МПа
| F2, см2 |
| 12-1 | 1,5 | 1,5 | 1,6 | 2,0 | ||
| 12-2 | 1,8 | 1,2 | 1,5 | 2,5 | ||
| 12-3 | 1,6 | 1,0 | 1,4 | 3,0 | ||
| 12-4 | 1,62 | 1,0 | 1,2 | 3,5 |
Задача №13
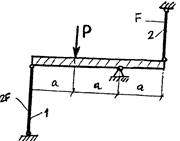
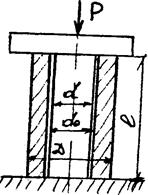 Опорное устройство (рис. 21) стенда для обкатки тракторов представляет собой круглый стальной стержень диаметром d, вставленный в трубу из алюминиевого сплава размерами d0, Д. Определить напряжения, возникающие в стержне и трубе, если они через жёсткую плиту сжимаются силой Р (в расчётах применять Ес=2*105 МПа, Еа=0,7*105 МПа)
Опорное устройство (рис. 21) стенда для обкатки тракторов представляет собой круглый стальной стержень диаметром d, вставленный в трубу из алюминиевого сплава размерами d0, Д. Определить напряжения, возникающие в стержне и трубе, если они через жёсткую плиту сжимаются силой Р (в расчётах применять Ес=2*105 МПа, Еа=0,7*105 МПа)
| № | Р, кН | d, мм | d0, мм | Д, мм | l,м |
| 13-1 | 20,0 | 22,0 | 1,2 | ||
| 13-2 | 25,0 | 27,0 | 1,4 | ||
| 13-3 | 13,5 | 37,0 | 1,5 | ||
| 13-4 | 40,0 | 42,0 | 1,0 |
Рис. 21
Задача №14
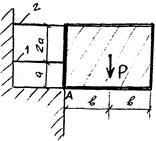 Емкость для ГСМ (воды) опирается в шарнире А и поддерживается двумя стальными растяжками 1 и 2, изготовленными из 2х одинаковых уголков (рис. 22).
Емкость для ГСМ (воды) опирается в шарнире А и поддерживается двумя стальными растяжками 1 и 2, изготовленными из 2х одинаковых уголков (рис. 22).
Определить напряжения в этих растяжках если:
| № | Р, кН | a, м | в, м | Номер уголка |
| 14-1 | 0,5 | 3,0 | 63х63х6 | |
| 14-2 | 1,0 | 4,0 | 80х80х8 | |
| 14-3 | 0,8 | 2,5 | 70х70х5 |
Рис. 22
Задача №15

Настенный поворотный кран (рис. 23) представляет собой жёсткую балку АВ, поддерживаемую двумя растяжками 1 и 2 изготовленными из стали с пределом текучести  , круглого поперечного сечения диаметром d.
, круглого поперечного сечения диаметром d.
Определить допускаемую нагрузку для этого крана, исходя из прочности растяжек, обеспечивая требуемый запас прочности «К».
| № | а, м | 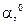
| 
| d, мм |  , МПа , МПа
| К |
| 15-1 | 1,5 | |||||
| 15-2 | 2,0 | 1,5 | ||||
| 15-3 | 2,5 | 1,4 | ||||
| 15-4 | 3,0 |
Рис.23
Задача №16

Сцепка состоит из 2-х одинаковых стальных стержней, изготовленных из 2-х равнобоких уголков. Определить номер уголка, если на сцепку действует внешняя нагрузка, равная Р, а для материала стержней допускаемое напряжение равно  .
.
| № | Р, кН | 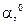
| l, м |  ,МПа ,МПа
|
| 16-1 | 40,0 | 1,5 | ||
| 16-2 | 75,0 | 1,8 | ||
| 16-3 | 60,0 | 1,2 |
Рис.24
Задача №17
 Сцепка состоит из 5-ти одинаковых стальных стержней (рис. 25). Определить усилия в стержнях и по наиболее нагруженному стержню подобрать трубчатое сечение при допускаемое напряжении материала стержней
Сцепка состоит из 5-ти одинаковых стальных стержней (рис. 25). Определить усилия в стержнях и по наиболее нагруженному стержню подобрать трубчатое сечение при допускаемое напряжении материала стержней  .
.
| № | Р, кН | С=d/Д |  ,МПа ,МПа
| а, м |
| 17-1 | 0,75 | 1,0 | ||
| 17-2 | 0,80 | 1,2 | ||
| 17-3 | 0,85 | 1,4 | ||
| 17-4 | 0,70 | 0,80 |
Рис. 25
Задача №18
 Квадратная жёсткая плита стола для разборки автотракторных двигателей (рис. 26) опирается на 4 симметрично расположенные стальные стойки одинаковой длины и одинакового поперечного сечения (швеллер). Определить величину усилия в каждой стойке при заданной внешней нагрузке Р, а также № швеллера при допустимом напряжении
Квадратная жёсткая плита стола для разборки автотракторных двигателей (рис. 26) опирается на 4 симметрично расположенные стальные стойки одинаковой длины и одинакового поперечного сечения (швеллер). Определить величину усилия в каждой стойке при заданной внешней нагрузке Р, а также № швеллера при допустимом напряжении  .
.
| № | Р, кН | a, м | в, м |  ,МПа ,МПа
|
| 18-1 | 0,8 | 0,25 | ||
| 18-2 | 1,2 | 0,40 | ||
| 18-3 | 1,5 | 0,30 |
Рис. 26
Задача №19

Жесткая плита опирается шарнирно в точке «С» и поддерживается двумя стальными стойками указанных размеров (рис. 27). Определить температурные напряжения в обоих стержнях, если будет подвергаться нагреву только 1 стержень на 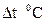 .
.
| Позиция | 1 стойка | 2 стойка | 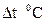 . .
| а, м | в, м | 
| ||
| F1, см2 | l1,м | F2, см2 | L2, м | |||||
| 19-1 | 5,0 | 1,5 | 7,5 | 1,2 | 1,5 | 3,0 | 12,5 | |
| 19-2 | 6,0 | 1,8 | 12,0 | 1,5 | 1,2 | 3,6 | 12,5 | |
| 19-3 | 8,0 | 2,0 | 12,0 | 1,6 | 1,4 | 3,5 | 12,5 | |
| 19-4 | 4,0 | 2,2 | 8,0 | 1,4 | 1,3 | 2,6 | 12,5 |
Рис. 27
Задача № 20

Определить температурные напряжения в стальной распорке при нагреве её на 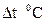 (рис. 28). Коэф. линейного расширения стали
(рис. 28). Коэф. линейного расширения стали 
| № | а, м | в, м | 
| F, см2 | 
|
| 20-1 | 0,8 | 2,2 | 2,0 | 15,0 | |
| 20-2 | 1,0 | 2,0 | 2,5 | 20,0 | |
| 20-3 | 1,2 | 2,4 | 1,5 | 25,0 | |
| 20-4 | 1,2 | 3,0 | 3,0 | 40,0 |
Рис. 28
Задача № 21

В подвеске (рис. 29) состоящей из 3-х стальных стержней с одинаковой площадью поперечного сечения нагреву на  , при эксплуатации подвергаются только крайние (1 и 3) стержни. Определить температурные напряжения во всех стержнях, если:
, при эксплуатации подвергаются только крайние (1 и 3) стержни. Определить температурные напряжения во всех стержнях, если:
Рис.29
| Позиция | 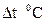 . .
| 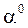
| h, м | F, см2 | 
|
| 21-1 | 1,6 | 12,5 | |||
| 21-2 | 1,8 | 12,0 | |||
| 21-3 | 2,0 | 11,6 | |||
| 21-4 | 1,5 | 12,5 |
Задача №22

| позиция | ∆t,0С | l,м | ac*10-6 | aм*10-6 | aа*10-6 |
| 22-1 | 1,0 | 12,0 | 16,5 | 21,6 | |
| 22-2 | 0,8 | 12,5 | 19,0 | 24,0 | |
| 22-3 | 0,9 | 11,6 | 22,0 | 22,0 |
В каком из указанных стержней (рис. 30) одинаковой длинны и поперечного сечения, возникнут наибольшие температурные напряжения при их нагреве, если:
Рис.30
Задача №23
 В заданной конструкции (рис31), представляющий собой жесткую шарнирно-опертую балку с 2мя поддерживающими стальными тягами одинакового поперечного сечения F, 2ой стержень был изготовлен короче требуемой длины на величину d. Определить монтажные нормальные напряжения в обоих стержнях, которые возникнут при сборке конструкции, если:
В заданной конструкции (рис31), представляющий собой жесткую шарнирно-опертую балку с 2мя поддерживающими стальными тягами одинакового поперечного сечения F, 2ой стержень был изготовлен короче требуемой длины на величину d. Определить монтажные нормальные напряжения в обоих стержнях, которые возникнут при сборке конструкции, если:
Рис.31
| Позиция | a, м | l1,м | F1,см2 | l2,м | F2,см2 | d,мм |
| 23-1 | 1,0 | 1,5 | 5,0 | 1,8 | 5,0 | 1,0 |
| 23-2 | 1,5 | 1,8 | 8,0 | 2,2 | 8,0 | 1,2 |
| 23-3 | 1,8 | 2,0 | 4,5 | 2,5 | 4,5 | 1,5 |
| 23-4 | 2,2 | 2,5 | 10,0 | 3,0 | 10,0 | 2,0 |
Задача №24

В заданной конструкции (рис 32) 2й стержень был изготовлен короче требуемой длины на величину d. Определить величину монтажных напряжений, возникающих в стержнях при сборке конструкций, если:
Рис.32
| позиция | а,м | l1=l3 | F1=F3,см | l2,м | F2,см | d, мм |
| 24-1 | 1,5 | 1,5 | 2,0 | 2,0 | 3,0 | 1,0 |
| 24-2 | 2,0 | 1,8 | 2,5 | 2,4 | 3,75 | 1,2 |
| 24-3 | 2,5 | 1,2 | 4,0 | 1,6 | 6,0 | 1,5 |
Задача №25

В подвеске колеса плуга, изображенной на (рис33) средний стержень был изготовлен длиннее требуемой длины на величину d. Определить монтажные напряжения которые возникнут во всех 3х стержнях после сборки. Все стержни стальные, одинаковой площадью поперечного сечения F.
| Позиция | h,м | a,0 | d,мм | F,см |
| 25-1 | 0,5 | 0,8 | 5,0 | |
| 25-2 | 0,6 | 1,0 | 4,0 | |
| 25-3 | 0,8 | 1,2 | 2,5 | |
| 25-4 | 1,0 | 1,5 | 6,0 |
Рис.33
Задача №26

В подвеске (рис34) 3й стержень был изготовлен короче требуемой длины на величину d. Определить монтажные напряжения во всех 3х стержнях после сборки конструкции, стержни стальные, с одинаковой площадью поперечного сечения F.
| Позиция | a,0 | h,м | l3,м | d,мм | F,см |
| 26-1 | 1,5 | 2,0 | 0,8 | 5,0 | |
| 26-2 | 1,8 | 1,5 | 1,0 | 4,0 | |
| 26-3 | 1,2 | 1,8 | 1,4 | 8,0 | |
| 26-4 | 2,0 | 1,6 | 1,2 | 10,0 |
Рис.34
Задача № 27
 Подобрать размеры стальных стержней 1 и 2, поддерживающих шарнирно - опертую жесткую балку АВ и нагруженную нагрузкой интенсивностью q (рис. 35)
Подобрать размеры стальных стержней 1 и 2, поддерживающих шарнирно - опертую жесткую балку АВ и нагруженную нагрузкой интенсивностью q (рис. 35)
Допускаемое напряжение для материала стержней  . Определить так же из условия прочности, какие потребуются размеры поперечного сечения 1 стержня, если убрать 2
. Определить так же из условия прочности, какие потребуются размеры поперечного сечения 1 стержня, если убрать 2  стержень.
стержень.
| Позиция | 
|
 , м , м
|  , МПа , МПа
| Форма сечения |
| 27-1 | 1,0 | (швеллер) | ||
| 27-2 | 1,2 | Два равнобоких уголка | ||
| 27-3 | 1,4 |  Кольцо Кольцо
| ||
| 27-4 | 0,8 | (круг) | ||
| 27-5 | 0,6 | (квадрат) |
Рис.35.
Задача № 28
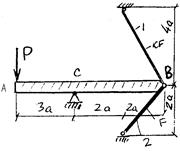 Жесткая балка АВ, шарнирно – опертая в точке “С”, поддерживается двумя стальными стержнями (рис. 36). Определить допустимую нагрузку на конструкцию из условия прочности стержней, если:
Жесткая балка АВ, шарнирно – опертая в точке “С”, поддерживается двумя стальными стержнями (рис. 36). Определить допустимую нагрузку на конструкцию из условия прочности стержней, если:
| Позиция |  , м , м
|  , МПа , МПа
| К | 
|
| 28-1 | 0,5 | 1,5 | ||
| 28-2 | 0,8 | 2,0 | ||
| 28-3 | 1,0 | 1,4 | ||
| 28-4 | 1,2 | 1,2 | ||
| 28-5 | 1,5 | 1,8 |
Рис. 36
Задача № 29
 Короткая деревянная стойка длиной
Короткая деревянная стойка длиной  с квадратным сечением размером “a”, усиленная четырьмя равнобокими уголками сжимается силой Р, передающейся через жесткую плиту (рис. 37). Определить напряжения, возникающие в уголках, если:
с квадратным сечением размером “a”, усиленная четырьмя равнобокими уголками сжимается силой Р, передающейся через жесткую плиту (рис. 37). Определить напряжения, возникающие в уголках, если:
| Позиция | Р, кН |  . м . м
|
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-12 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |