


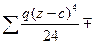
 (23)
(23)




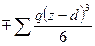 (24)
(24)
Здесь 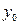 и
и  - прогиб и угол поворота в начале системы координат, начало координат всегда располагается в левом крайнем сечении балки;
- прогиб и угол поворота в начале системы координат, начало координат всегда располагается в левом крайнем сечении балки;
Z – расстояние от начала координат до сечения, где определяется прогиб и угол поворота;
а, в, с, d – расстояние от начала координат до места приложения соответствующих внешних сил m, p, q.
МЕТОДОМ МОРА – ВЕРЕЩАГИНА
Для этого строятся эпюры изгибающих моментов от заданной внешней нагрузки  (рис. 43, а), от единичной силы
(рис. 43, а), от единичной силы  (рис. 43б) при определении прогиба и единичного момента -
(рис. 43б) при определении прогиба и единичного момента -  (рис. 43в) при вычислении угла поворота, и производится “перемножение” соответствующих эпюр, т.е. с одной эпюры берем ее площадь
(рис. 43в) при вычислении угла поворота, и производится “перемножение” соответствующих эпюр, т.е. с одной эпюры берем ее площадь  , а с другой – ординату
, а с другой – ординату  , расположенную под центром тяжести взятой площади.
, расположенную под центром тяжести взятой площади.






 (26)
(26)


 (27)
(27)
Рис. 43
Основные правила перемножения эпюр:
- результат положителен, если эпюры расположены по одну сторон от оси балки, если по разные стороны – результат отрицательный;
- положительный результат перемножения эпюр свидетельствует о том, что направление перемещения (линейного и углового) совпадает с направлением единичных сил, при отрицательном результате – противоположны направлению единичных сил;
- если обе эпюры ( и
и  ) линейны, то не имеет принципиального значения с какой эпюры брать площадь
) линейны, то не имеет принципиального значения с какой эпюры брать площадь  , с какой ординату
, с какой ординату  ;
;
- если одна из эпюр криволинейна (это  ), то площадь обязательно берется с нее;
), то площадь обязательно берется с нее;
- если сложно вычислять площадь эпюры, определить координаты центра тяжести ее и ординату  , то при перемножении эпюр
, то при перемножении эпюр  и
и  используется прием Симсона (формула 28) (рис. 44).
используется прием Симсона (формула 28) (рис. 44).

 (28)
(28)
 А, В, С – ординаты с грузовой эпюры
А, В, С – ординаты с грузовой эпюры 
а, b, с – тоже с единичной эпюры 
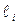 - спина i-го участка балки
- спина i-го участка балки
Рис. 44.
4.1. ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ.
ЗАДАЧА № 32.
 Для заданного вала (рис. 45) построить эпюру крутящих моментов и определить из условия прочности и жесткости требуемый диаметр. Вал изготовлен из стали 45, имеющей
Для заданного вала (рис. 45) построить эпюру крутящих моментов и определить из условия прочности и жесткости требуемый диаметр. Вал изготовлен из стали 45, имеющей  = 320 МПа, а запас по прочности К = 2,5. Допускаемый относительный угол закручивания
= 320 МПа, а запас по прочности К = 2,5. Допускаемый относительный угол закручивания  . На валу расположены 4 шкива, передающие мощность
. На валу расположены 4 шкива, передающие мощность  = 15 КВт,
= 15 КВт,  =45 КВт,
=45 КВт, 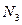 =20 КВт,
=20 КВт, 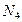 =10 КВт при оборотах вала n = 955 об/мин.
=10 КВт при оборотах вала n = 955 об/мин.
Рис.45
РЕШЕНИЕ
1. Определяем величину внешних скручивающих моментов, перед каждым шкивом (через мощность и обороты вала)
 (кнм) (29)
(кнм) (29)
где N – мощность, КВт; n – число оборотов в минуту.

 кнм;
кнм;  кнм;
кнм;
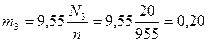 кнм;
кнм;  кнм
кнм
2. Строим эпюру крутящих моментов, разбив вал на участки I, II, III, применяя метод сечения и приняв следующее правило знаков для крутящего момента 
если смотреть на оставленную часть вала со стороны сечения, то
 ;
; 

На эпюре  видно, что в сечениях, где приложены внешние моменты получаются скачки, равные по величине этим моментам. Максимальная величина
видно, что в сечениях, где приложены внешние моменты получаются скачки, равные по величине этим моментам. Максимальная величина
 = 0,30 кнм.
= 0,30 кнм.
3. Определяем диаметр вала по условиям прочности и жесткости, применяя формулы (20), предварительно определив допускаемое касательное напряжение
 Мпа
Мпа


здесь 
 переведен в
переведен в 

Из полученных  значений принимаем диаметр вала d = 35 мм, обеспечивая тем самым требования и жесткости и прочности.
значений принимаем диаметр вала d = 35 мм, обеспечивая тем самым требования и жесткости и прочности.
ЗАДАЧА № 33. Для заданного ступенчатого кронштейна, нагруженного внешними окручивающими моментами m1 = 10 кНм и m2 = 30 кНм и защемленного с обоих концов, требуется построить эпюру крутящих моментов Мк и при допускаемом касательном напряжении [  ] = 80. Определить диаметры сплошной и кольцевой частей (рис. 46). В кольцевой части D = 2d, d0 = 0,8d, т. е. c =
] = 80. Определить диаметры сплошной и кольцевой частей (рис. 46). В кольцевой части D = 2d, d0 = 0,8d, т. е. c =  = 0,4
= 0,4
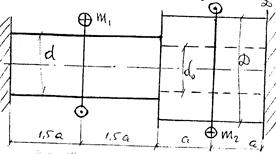
Рис.46.
Решение.
 1. Обозначив опорные моменты через m
1. Обозначив опорные моменты через m 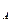 и m
и m  , и составив уравнение равновесия в виде
, и составив уравнение равновесия в виде 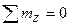 (рис. 47а) (-mA+m1-m2+mB = 0) мы убеждаемся, что заданная система является статически неопределимой.
(рис. 47а) (-mA+m1-m2+mB = 0) мы убеждаемся, что заданная система является статически неопределимой.
Превратим ее в статически определимую, отбросив например опору "В", заменив ее действие опорным моментом " m  ". Отбросив опору "В", мы дали возможность сечению В поворачиваться под действием всех внешних моментов, но ведь в заданной системе сечение В жестко защемлено, поворота не имеет. Отразим этот факт, составив уравнение перемещений:
". Отбросив опору "В", мы дали возможность сечению В поворачиваться под действием всех внешних моментов, но ведь в заданной системе сечение В жестко защемлено, поворота не имеет. Отразим этот факт, составив уравнение перемещений:
 =0 (30)
=0 (30)
Рис. 47
Используя закон Гука при кручении  запишем
запишем





Сократив на “a” и жесткость “  ”, получим
”, получим
 (31)
(31)
Здесь  и
и  - полярные моменты инерции сплошной и кольцевой частей кронштейна. Их соотношение равно
- полярные моменты инерции сплошной и кольцевой частей кронштейна. Их соотношение равно
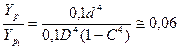
Решив уравнение (31), получим значение опорного момента 

Тогда из уравнения равновесия определяем величину опорного момента

Полученные положительные значения опорных моментов  и
и  говорит о том, что их направление было выбрано верно.
говорит о том, что их направление было выбрано верно.
2. Разбиваем заданную систему на участки I, II, III, IV (рис. 47б). Границами участков являются сечения, где приложены внешние моменты и меняется сечение. Строим эпюры крутящих моментов (рис. 47в) применяя метод сечений


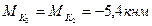

3. Из условия прочности при кручении определяем диаметры сплошной и кольцевой частей кронштейна, предварительно определив, как действуют наибольшие касательные напряжения


Таким образом, наибольшие касательные напряжения действуют в значениях 2  участка, их и сравниваем с допускаемыми
участка, их и сравниваем с допускаемыми 
Отсюда диаметр сплошной части d равен 
Тогда размеры кольцевой части кронштейна составят  ,
, 
ЗАДАЧА № 34
 Для заданной балки построить эпюру поперечных сил
Для заданной балки построить эпюру поперечных сил  и изгибающих моментов
и изгибающих моментов  и подобрать размеры поперечного сечения в виде швеллера при допускаемом напряжении
и подобрать размеры поперечного сечения в виде швеллера при допускаемом напряжении  =150 Мпа.
=150 Мпа.
Рис.48
РЕШЕНИЕ
1. Введем построение эпюр  и М по участкам справа, со стороны свободного конца (рис 48а и б)
и М по участкам справа, со стороны свободного конца (рис 48а и б)
первый участок 
 ,
, 
второй участок  ,
, 


третий участок 
 ;
;
 ,
, 
Определим координату  сечения, где поперечная сила проходит через нуль, в этом сечении изгибающий момент
сечения, где поперечная сила проходит через нуль, в этом сечении изгибающий момент  имеет экстремальное значение
имеет экстремальное значение

 ,
, 




2. Из условия прочности на прямом изгибе определяем размеры (номер швеллера) сечения балки  ,
, 
ПО сортаменту на швеллера Гост 8240 – 82[1] и учитывая, что сечение состоит из  швеллеров, принимаем швеллер № 10, которого
швеллеров, принимаем швеллер № 10, которого  .
.
ЗАДАЧА № 35

Для заданно шарнирно опертой балки построить эпюры поперечных сил и изгибающих моментов  и определим с каким запасом прочности она будет работать (рис. 49), если
и определим с каким запасом прочности она будет работать (рис. 49), если 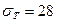 b=60мм, h=140мм, а=35мм.
b=60мм, h=140мм, а=35мм.
Рис. 49
РЕШЕНИЕ
1. Определяем сначала опорные реакции из условия равновесия балки

 ;
; 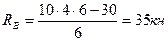

 ;
; 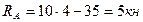
Проверка 
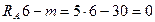
Следовательно реакции определены верно.
2. Разбиваем балку на участки I, II, III, IV, границами участков являются сечения, где приложены внешние силы. С помощью метода сечения строим эпюры  и
и  (рис. 49а и б)
(рис. 49а и б)
первый участок 
 ,
, 
второй участок  ,
, 

третий участок (рассматриваем правую часть); 



четвертый участок 

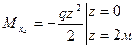
3. По эпюре  видим, что наибольший изгибающий момент равен 20 кНм.
видим, что наибольший изгибающий момент равен 20 кНм.
4. Вычисляем величину максимальных нормальных напряжений, действующих в балке, по формуле (22), предварительно определив осевой момент сопротивления заданного сечения через осевой момент инерции


Тогда при 
 , а напряжение
, а напряжение 
5. Запас прочности балки определяем из условия прочности
 ;
;  , что вполне достаточно.
, что вполне достаточно.
ЗАДАЧА № 36
Для заданной двутавровой балки (рис. 50) построить эпюры  и
и  , подобрать сечение при
, подобрать сечение при  =160 МПа и проверить его на прочность по касательным напряжениям, а так же определить прогиб в точке “C” и угол поворота сечения “K” двумя способами: методом начальных параметров и методом Море – Верещагина.
=160 МПа и проверить его на прочность по касательным напряжениям, а так же определить прогиб в точке “C” и угол поворота сечения “K” двумя способами: методом начальных параметров и методом Море – Верещагина.
РЕШЕНИЕ.
 1. Определяем сначала опорные реакции из условия равновесия
1. Определяем сначала опорные реакции из условия равновесия


 ;
; 

 ;
;
Рис. 50


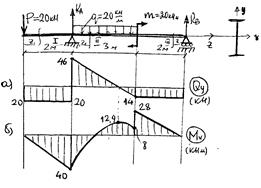
2. Строим эпюры  и
и  , по участкам (рис 50а и б)
, по участкам (рис 50а и б)
первый участок 
 ,
, 
второй участок 

координата сечения, где 


третий участок 
 ;
; 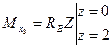
3. Подбираем двутавровое сечение балки из условия прочности по нормальным напряжениям  , отсюда
, отсюда  .
.
По сортаменту ГОСТ 8239 – 89 принимаем двутавр № 22а, у которого 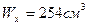 ,
,  ,
,  ,
, 
4. Применяем выбранное сечение на прочность по касательным напряжениям, применяя формулу Д.И. Жуковского.

Допускаемое касательное напряжение обычно равно 
Следовательно, прочность по касательным напряжениям вполне обеспечена, ибо 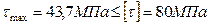
5. Определяем прогиб “  ” в, т “C” и угол поворота
” в, т “C” и угол поворота  сечения “K” (в нашем примере они совпадают) методом начальных параметров. Для этого помещаем начало координат в левое крайнее сечение и записываем
сечения “K” (в нашем примере они совпадают) методом начальных параметров. Для этого помещаем начало координат в левое крайнее сечение и записываем


В этом уравнении оба начальных параметра 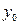 и
и  неизвестны. Для их определения составляем уравнения прогибов для сечений над опорами А и В, где ясно, что они равны 0.
неизвестны. Для их определения составляем уравнения прогибов для сечений над опорами А и В, где ясно, что они равны 0.





Подставив значения координат и внешних сил, получим два уравнения


Решив их, получим 

Тогда прогиб сечения “C” будет равен


Угол поворота этого же сечения



6. Определяем прогиб сечения “C” и угол поворота сечения ”K” методом Мора – Верещагина, для этого дополнительно к эпюре изгибающих моментов от заданной нагрузки (рис. 51а) строим эпюры  и
и  от единичных сил (51 б и в) и производим перемножение соответствующих эпюр. В результате получим (см. выражение 28) прогиб
от единичных сил (51 б и в) и производим перемножение соответствующих эпюр. В результате получим (см. выражение 28) прогиб
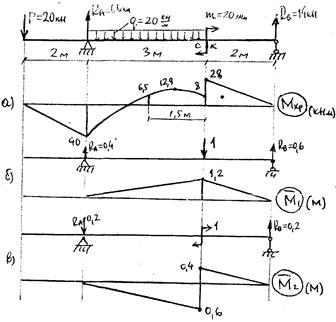
Рис. 51
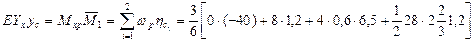

т. е. практически получили одинаковое с методом начальных параметров значение прогиба.
Угол поворота

 тоже практически совпало со значением, полученным по методу начальных параметров.
тоже практически совпало со значением, полученным по методу начальных параметров.
Положительное значение результатов перемножения эпюр свидетельствует, что линейные и угловые перемещения сечений “C” и “K” совпадают с направлениями единичных сил (прогиб вниз, а поворот по часовой стрелке).
ВАРИАНТЫДОМАШНИХ ЗАДАНИЙ
В домашнее задание № 3 входит решение 2  задач на кручение и одной задачи на прямой изгиб. Номер задач, расчетные схемы и исходные данные в соответствии со своим вариантом принимаются по таблицам № 3 (1 – ая задача), № 4 (2 – ая задача) и № 5 (3 – ая задача).
задач на кручение и одной задачи на прямой изгиб. Номер задач, расчетные схемы и исходные данные в соответствии со своим вариантом принимаются по таблицам № 3 (1 – ая задача), № 4 (2 – ая задача) и № 5 (3 – ая задача).
При выполнении домашней работы требуется!
В 1 – ой задаче:
- построить эпюру крутящих моментов;
- определить диаметры круглого сплошного или кольцевого сечения из условий прочности и жесткости или максимальное касательное напряжение и запас прочности “K”;
Во 2 – ой задаче:
- раскрыть статическую неопределимость заданной системы, составить необходимое число уравнений перемещений;
- построить эпюру крутящих моментов;
- из условий прочности определить требуемые диаметры заданного сечения стержня.
В 3 – ей задаче:
- построить эпюры поперечных сил  и изгибающих моментов М для указанной балки;
и изгибающих моментов М для указанной балки;
- подобрать из условий прочности размеры поперечного сечения заданной формы;
- определить прогиб в сечении “C” и угол поворота сечения “K” методом начальных параметров и методом Мора – Верещагина.
Таблица 3