Геометрические характеристики плоских сечений – задание № 2.

 

Прочность и жесткость элементов конструкций при различных видах воздействия внешних сил, особенно при деформациях кручения, изгиба, сложного сопротивления и др. зависит не только от материала стержня, но и от формы и размеров его поперечного сечения и расположения сечения относительно направления действия внешних нагрузок. Это учитывается рядом геометрических характеристик плоского поперечного сечения, основными из которых являются (рис. 39):

площадь (5)

Рис.39

 

статические моменты

, (6)

осевые моменты инерции

, (7)

Центробежный момент инерции 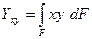(8)

Полярный момент инерции (9)

Координаты центра тяжести сечения определяются через статические моменты

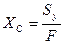, (10)

Естественно, все вышеуказанные характеристики зависят от положения осей и они вычисляются через размеры поперечного сечения (рис. 40):

(11)

(12)

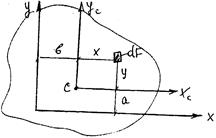
(13)

Среди множества центральных осей есть, очевидно, оси, относительно которых осевые моменты инерции принимают экстремальное (наибольшее и наименьшее) значение, а центробежный момент инерции равен нулю. Эти оси называются главными осями, их положение определяется –по формуле

Рис.40

(14)

Моменты инерции относительно главных осей, называемые главными моментами инерции, определяются выражением:

(15)

При выполнении расчетов на прочность, жесткость и устойчивость наибольший и определяющий интерес и представляет определение положения главных центральных осей и вычисление главных моментов инерции заданного поперечного сечения, которое обычно осуществляется в следующей последовательности:

- выбирается вспомогательная система координат;

- заданное сложное сечение разбивается на простые фигуры, обозначаются их координаты центров тяжести и собственные оси;

- во вспомогательной системе координат определяется положение общего центра тяжести сечения (по формуле 10);

- через общий центр тяжести проводят центральные оси (параллельно собственным осям) и вычисляют осевые (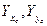 и центробежные ) моменты инерции относительно этих осей, используя правило параллельного перехода (формулы (11) – (13));

- по формуле (14) определяют угол , на который надо повернуть центральные оси, чтобы они стали главными осями (при >0 против часовой стрелки, при <0 по часовой стрелке);

- вычисляют величину главных моментов инерции сечения по формуле (15), обычно при , , .

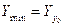Равномерность моментов инерции обычно см. 4. Все моменты инерции (кроме центробежного) величины суть положительные (подробнее см. пример решения).

 

Пример решения задачи

 

Для заданного поперечного сечения (рис. 41) опорного бруса зерносушилки, состоящего из швеллера № 24, уголка 80+80+8 и прямоугольного треугольника с размерами в=80 и h=150мм. Определить положение главных центральных осей и вычислить главные моменты инерции.

 

Решение

1. Выбираем вспомогательную систему координат x,y так, чтобы все сечение находилось в положительной четверти (для удобства вычислений);

 

 

2. 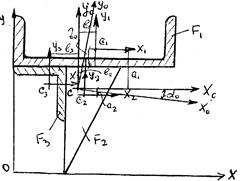Разбиваем заданное сечение на простые фигуры с площадями - швеллер № 24; - треугольник; - уголок;

3. Обозначаем центры тяжести, собственные оси инерции каждой фигуры, выписываем из сортаментов по ГОСТ 8240-72 и ГОСТ-8505-86 (для швеллера и уголка), а для треугольника считаем, необходимые данные :

 

Рис. 41

 

Швеллер - , ,

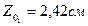(обращаем внимание, что заданный швеллер по отношению к гостовскому повернут на 90 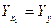и и из сортамента).

Уголок , , , 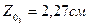В=70 мм,

Треугольник - ; ; ;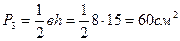

 

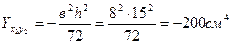
4. Определяем координаты общего центра тяжести

Здесь - расстояние от оси yдо центров тяжести каждой фигуры

здесь - расстояние от оси Х до центров тяжести каждой фигуры

 

5. Через общий центр тяжести (т.с.) проводим параллельно собственным осям каждой фигуры центральные оси вычисляем осевые и центробежные моменты инерции относительно их

=208+30,6(17,42-12,53) +750+60(12,53-10) +73,36+12,3(12,73-12,53) =

=2147,5 см

Здесь - расстояние соответственно между параллельными осями

и , и , и =4,89 см, =-2,53 см, =0,2 см.

=2900+30,6(12-10,5) +213,3+60(10,7-10,5) +73,36+12,3(10,5-5,73) =

=3537,8 см

Здесь 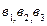- расстояние соответственно между параллельными осями

и 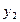, и , и =1,5 см, =0,2 см, =-4,77 см.

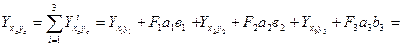
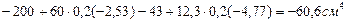
Здесь =0, т.к. собственные оси для швеллера являются главными.

6. Определяем положение главных центральных осей

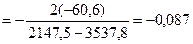
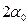=-5

Следовательно, поворачиваем центральные оси по часовой стрелке на , чтобы они стали главными центральными осями инерции.

 

 

7. Вычисляем главные центральные моменты инерции, применив формулу (15)

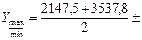
см (поскольку )

=2842б6-697,86=2144,8 см

Проверка:

3540,4+2144,8=2147,8+3537,8 (см) . Следовательно, расчет выполнен правильно.

 

Варианты домашних заданий

В домашнее задание № 2 входит решение 2 задач по определению геометрических характеристик плоских поперечных сечений (см. таблицу 2):

1. Сечение состоит из простых фигур;

2. Сечение составлено из прокатных профилей.

Таблица 2

Варианты домашнего задания № 2

Вариант	Форма сечения 1	Размеры в мм	Форма сечения 2	Профили
а	Б	в	г	А	В	С
							60х60х6		-
					45х45х5		-
					90х90х10		-
							-		-
					-		-
					-		-
							63х63х6		-
					45х45х5		-
					50х50х3		-
							-
					-
					-
							120х120х10		-
					160х160х20		-
					100х100х10		-
							-
					-
					-
							-
					-
					-
					-		100х100х10		-
				-	90х90х9		-
				-	120х120х10		-
									-
							-
							-