Необходимо рассмотреть элементы участка, предшествующие 5-му элементу, чтобы понять, можно ли его принять за скоростной подъем. Видим, что данному элементу предшествуют горизонтальные участки и спуски. Предполагаем, что поезд сможет развить достаточно высокую скорость и пройти этот элемент с использованием кинетической энергии, и его скорость к концу элемента не снизится ниже расчетной скорости локомотива. Следовательно, принимаем 5-й элемент профиля пути в качестве скоростного, а в качестве расчетного подъема – 6-й элемент профиля (i = 8 ‰, s = 5500 м).
Данный профиль участка можно отнести к тому варианту профиля, в котором за расчетный принимается менее крутой подъем большой протяженности, а подъем с максимальной крутизной принимается за скоростной.
Поскольку на расчетном и скоростном подъемах отсутствуют кривые, то их результирующие величины уклонов будут равняться их действительному уклону, т.е.
Определение массы состава по расчетному подъему. Масса состава Q определяется по формуле (3.1) из условия равенства расчетной касательной силы тяги локомотива силам сопротивления движению поезда при расчетной скорости на расчетном подъеме.
Касательная сила тяги тепловоза ТЭ3 F кр и его масса P приведены в задании (таблица 15.2): F кр = 396300 Н; P = 254 т.
Величина расчетного подъема определена ранее: i р= 8 ‰.
Основное удельное сопротивление движению локомотива (для режима тяги) 
и состава 
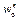определим по формулам (3.2)–(3.15) из условия, что поезд движется по звеньевому пути с расчетной скоростью v = v р = 20,5 км/ч.
Основное удельное сопротивление движению локомотива
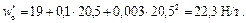
Для определения основного удельного сопротивления движению состава по формуле (3.6) определим основное удельное сопротивление движению каждого типа вагонов в отдельности по формулам (3.7), (3.9), (3.11). Предварительно определим осевую нагрузку для каждого типа вагонов по формулам (3.13) – (3.15).
По заданию массы вагонов брутто равны: q 4 = 80 т; q 6 = 120 т; q 8 = 160 т.
Тогда
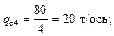
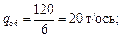
Основное удельное сопротивление движению 4-осного вагона
Основное удельное сопротивление движению 6-осного вагона
Основное удельное сопротивление движению 8-осного вагона
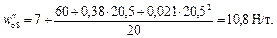
Основное удельное сопротивление движению состава с учетом доли вагонов (по массе) каждого типа (α4 = 0,73; α6 = 0,05; α8 = 0,22)
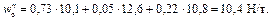
Масса состава
Округляем полученное значение в соответствии с ПТР до 50 т. Принимаем Q = 4100 т.
Проверка полученной массы состава на прохождение скоростного подъема. Проверка на преодоление элементов профиля большей крутизны, чем расчетный подъем, заключается в расчете скорости движения поезда для всех подъемов, крутизна которых превышает крутизну расчетного подъема. В нашем случае такой элемент только один – скоростной подъем крутизной уклона i ск= 11 ‰ и протяженностью s = 1400 м.
Для проверки массы состава на преодоление скоростного подъема определим путь, который может преодолеть поезд при движении по подъему с уклоном +11 ‰ в режиме тяги на номинальной мощности (максимальная позиция контроллера машиниста) при падении скорости с максимально допустимой до расчетной. За максимально допустимую скорость примем ограничение по состоянию пути, равное 80 км/ч.
Принимаем интервал изменения скорости от 80 до 70 км/ч. Средняя скорость на заданном интервале по формуле (4.6)
По тяговой характеристике тепловоза ТЭ3 (см. рисунок 15.1) определяем касательную силу тяги. При скорости 75 км/ч F к = 100000 Н.
Удельную касательную силу тяги определим по формуле (4.5):
Рассчитаем основное удельное сопротивление движению поезда по формулам (3.2) – (3.12), (4.4).
Основное удельное сопротивление движению локомотива
Основное удельное сопротивление движению 4-осного вагона
Основное удельное сопротивление движению 6-осного вагона
Основное удельное сопротивление движению 8-осного вагона
Средневзвешенное основное удельное сопротивление движению состава
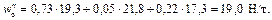
Основное удельное сопротивление движению поезда
Удельная равнодействующая сила в пределах выбранного интервала изменения скорости по формуле (4.3)
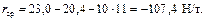
Путь, проходимый поездом при изменении скорости от 80 до 70 км/ч, по формуле (4.2)
Так как найденное значение пройденного пути меньше, чем длина проверяемого подъема (s = 1400 м), то следует продолжить расчеты. Результаты расчетов представим в таблице 15.4.
Таблица 15.4 – Расчет движения поезда по подъему с уклоном 11 ‰
| v 1, км/ч | v 2, км/ч | v ср, км/ч | F к, Н |  ,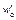
Н/т
|  ,
Н/т
|  ,
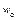Н
| r ср, Н/т |  ,
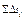м
|  ,
м
|
| 43,4 | 19,0 | 20,4 | –107,4 | ||||||
| 38,2 | 16,8 | 18,0 | –100,0 | ||||||
| 33,6 | 14,9 | 16,0 | –92,0 |
При снижении скорости с 80 до 50 км/ч поезд, двигаясь по подъему с уклоном 11 ‰, проходит путь 1622 м. Проверка массы состава на прохождение скоростного подъема выполняется (1622 > 1400), и массу корректировать нет необходимости.
Проверка массы состава на трогание с места. Прежде чем приступить к расчетам, необходимо определить уклон участка пути, на котором происходит трогание поезда (следует принять уклон станционных путей с максимальным подъемом). В нашем случае это элемент № 10 с крутизной уклона i тр = 1,5 ‰. Кривая на данном элементе отсутствует, т.е. дополнительного сопротивления от действия кривой нет.
Для проверки массы состава на трогание с места по формуле (5.1) определим массу состава, которую локомотив может взять с места. Для этого рассчитаем удельное сопротивление движению состава при трогании с места по формулам (5.2)–(5.5).
Удельное сопротивление троганию вагонов
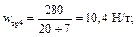
Удельное сопротивление движению состава при трогании
С учетом того, что касательная сила тяги локомотива при трогании по исходным данным равна F ктр = 571000 Н (не превышает максимальную силу на автосцепке, ограниченную величиной 930 кН), определим массу состава, которую локомотив может взять с места, по формуле (5.1):
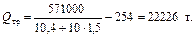
Так как масса состава при трогании больше расчетной массы состава (Q тр > Q), то проверка массы состава на трогание выполняется.
Проверка массы состава по длине приемоотправочных путей. На основании исходных данных длина приемоотправочных путей равна l поп = 1550 м. Сравним данную величину с длиной поезда, которую определим по формуле (6.1).
Для определения длины состава найдем количество 4, 6 и 8-осных вагонов по формуле (6.2):
По таблице 6.1 принимаем:
– четырехосные крытые и изотермические вагоны – l 4 = 15 м;
– шестиосные полувагоны – l 6 = 17 м;
– восьмиосные цистерны – l 8 = 21 м.
По формуле (6.3) определим длину состава:
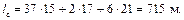
С учетом того, что длина локомотива l л = 34 м, определим длину поезда по формуле (6.1):
Длина поезда меньше длины приемоотправочных путей, следовательно, поезд уместится на них. Проверка выполняется.
Спрямление профиля пути на заданном участке. Произведем спрямление исходного профиля, представленного в таблице 15.3. Будем следовать алгоритму, предложенному в разделе 7.
1 Определим элементы профиля, которые спрямлять нельзя. Не спрямляют элементы 1, 10, 22 (остановочные пункты), 5 (скоростной подъем) и 6 (расчетный подъем). Помимо этого не будем спрямлять с другими элементами профиля 15-й и 19-й элементы, т.к. крутизна их уклонов значительно отличается от крутизны соседних элементов.
2 Определим возможные группы спрямляемых элементов. В нашем случае предварительно можно сгруппировать элементы между собой таким образом: 2-3-4, 7-8-9, 11-12-13-14, 16-17-18 и 20-21.
3 Производим проверку возможности спрямления. Произведем спрямление элементов 2-3-4.
По формуле (7.1)
По формуле (7.2) с учетом округления по ПТР
По условию (7.3) проверим возможность спрямления профиля:
– для 2-го элемента –
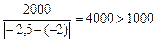(условие выполняется);
– для 3-го элемента –
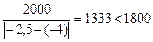(условие не выполняется).
Для 3-го элемента условие спрямления не выполняется, следовательно, спрямление данной группы элементов невозможно. Произведем спрямление элементов 2-3:
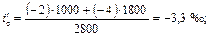
(условие выполняется);
(условие выполняется).
Так как для всех элементов условие спрямления выполняется, то можно элементы 2-3 спрямлять в один, длина которого 2800 м, а крутизна 
.
4 Произведем учет влияния кривых и определим приведенный уклон элементов спрямленного профиля. На 2-м приведенном элементе профиля располагается кривая (R кр= 1200 м, s кр = 600 м), фиктивный подъем от кривизны пути определим по формуле (7.4):
Приведенный уклон для данного элемента профиля по формуле (7.6)
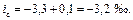
Дальнейшие расчеты аналогичны, и их результаты приведены в таблице 15.5.
Таблица 15.5 – Спрямленный профиль
| № элемента | Длина, м | Уклон, ‰ | Кривые | s с, м |  , ‰
|  , ‰
| i c, ‰ | 
| № приве-денно-го элемента | Примечание | |
| R кр, м | S кр, м | ||||||||||
| – | – | – | – | – | Ст. А | ||||||
| –2 | – | – | –3,3 | +0,1 | –3,2 | ||||||
| –4 | |||||||||||
| +0,4 | +0,4 | – | |||||||||
| +11 | – | – | – | – | +11 | – | v ск | ||||
| +8 | – | – | – | – | +8 | – | v р | ||||
| – | – | +0,7 | – | +0,7 | |||||||
| +2 | – | – | |||||||||
| – | – | ||||||||||
| +1,5 | – | – | – | – | +1,5 | – | Ст. Б | ||||
| – | – | – | – | – | |||||||
| –5 | –5 | +0,3 | –4,7 | – | |||||||
| –4 | – | – | –1,5 | +0,4 | –1,1 | ||||||
| –10 | – | – | – | – | –10 | – | |||||
| +1,8 | +0,3 | +2,1 | |||||||||
| +2,5 | |||||||||||
| – | – | – | – | – | |||||||
| –7 | – | – | – | – | –7 | – | |||||
| – | – | – | – | – | |||||||
| –4 | – | – | – | – | –4 | – | |||||
| –1 | – | – | – | – | –1 | – | Ст. В |
Расчет и построение диаграммы удельных равнодействующих сил. Для построения диаграммы удельных равнодействующих сил произведем расчеты, результаты которых внесем в таблицы.
Режим тяги. В первый столбец вносим значения скорости движения поезда от 0 до конструкционной скорости тепловоза ТЭ3 (100 км/ч) с интервалом 10 км/ч. Кроме того, дополнительно вносим значения скорости, соответствующие характерным точкам тяговой характеристики. В нашем случае – скорость перехода от ограничения по пусковому току на автоматическую характеристику (13 км/ч) и расчетная скорость (20,5 км/ч).
По тяговой характеристике тепловоза ТЭ3, приведенной на рисунке 15.1, и таблице 15.2 вносим значения касательной силы тяги, соответствующие скорости движения локомотива.
Так как поезд движется по звеньевому пути, то по формуле (3.2) определяем значения основного удельного сопротивления движению локомотива в режиме тяги 
для принятой из первого столбца скорости. Для скорости 0 принимаем значение, рассчитанное для 10 км/ч. По формуле (8.1) определяем основное сопротивление движению локомотива в режиме тяги.
Значения основного удельного сопротивления движению состава 
определяем по формулам (3.6), (3.7), (3.9), (3.11). Для скорости 0 принимаем значение, рассчитанное для 10 км/ч.
По формулам (8.2) и (8.3) определяем соответственно основное сопротивление движению состава и основное сопротивление движению поезда. А по формуле (8.4) – равнодействующую силу, действующую на поезд при движении в режиме тяги. Удельную равнодействующую силу, действующую на поезд при движении в режиме тяги по прямому горизонтальному участку пути, определяем по формуле (8.5).
Все результаты расчетов для режима тяги сводим в таблицу 15.6. По результатам расчета строим график удельных равнодействующих сил для режима тяги r т, представленный на рисунке 15.2 (графики удельных равнодействующих сил оформляются на листе миллиметровой бумаги формата А3 в заданном масштабе).
Таблица 15.6 – Расчет удельных равнодействующих сил для режима тяги
| v, км/ч | F к, Н |  ,
Н/т
|  ,
Н
|  ,
Н/т
|  ,
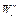Н
| W о, Н | R, Н | r т, Н/т |
| 20,3 | 9,5 | 121,0 | ||||||
| 20,3 | 9,5 | 121,0 | ||||||
| 20,8 | 9,7 | 120,8 | ||||||
| 22,2 | 10,3 | 82,0 | ||||||
| 20,5 | 22,3 | 10,4 | 79,9 | |||||
| 24,7 | 11,3 | 49,0 | ||||||
| 27,8 | 12,6 | 32,9 | ||||||
| 31,5 | 14,1 | 22,1 | ||||||
| 35,8 | 15,9 | 13,7 | ||||||
| 40,7 | 17,9 | 6,5 | ||||||
| 46,2 | 20,1 | –1145 | –0,3 | |||||
| 52,3 | 22,6 | –30944 | –7,1 | |||||
| 59,0 | 25,3 | –59716 | –13,7 |
Режим холостого хода. Основное удельное сопротивление движению локомотива в режиме холостого хода определяем по формуле (3.4). Для скорости 0 принимаем значение, рассчитанное для 10 км/ч. Основное сопротивление движению локомотива в режиме холостого хода определяем по формуле (8.6). Основное сопротивление движению поезда на холостом ходу определяем по формуле (8.7), а основное удельное сопротивление движению поезда – по формуле (8.8).
Результаты расчетов для холостого хода представляем в таблице 15.7, а график удельных равнодействующих сил в режиме холостого хода r х – на рисунке 15.2.
Таблица 15.7 – Расчет удельных равнодействующих сил для режимов холостого хода и торможения
| v, км/ч | w х, Н/т | W х, Н | W ох, Н | w ох, Н/т | φкр | b т, Н/т | r тс, Н/т | r тэ, Н/т |
| 25,5 | 10,4 | 0,360 | 752,4 | 386,6 | 762,8 | |||
| 25,5 | 10,4 | 0,339 | 708,5 | 364,7 | 718,9 | |||
| 26,0 | 10,7 | 0,333 | 696,0 | 358,7 | 706,7 | |||
| 27,6 | 11,3 | 0,322 | 673,0 | 347,8 | 684,3 | |||
| 20,5 | 27,7 | 11,4 | 0,321 | 670,9 | 346,9 | 682,3 | ||
| 30,5 | 12,4 | 0,309 | 645,8 | 335,3 | 658,2 | |||
| 34,0 | 13,8 | 0,297 | 620,7 | 324,2 | 634,5 | |||
| 38,3 | 15,5 | 0,288 | 601,9 | 316,5 | 617,4 | |||
| 43,2 | 17,5 | 0,280 | 585,2 | 310,1 | 602,7 | |||
| 48,9 | 19,7 | 0,273 | 570,6 | 305,0 | 590,3 | |||
| 55,2 | 22,1 | 0,267 | 558,0 | 301,1 | 580,1 | |||
| 62,3 | 24,9 | 0,262 | 547,6 | 298,7 | 572,5 | |||
| 70,0 | 27,9 | 0,257 | 537,1 | 296,5 | 565,0 |
При построении графика учитываем направление действия силы, и значения основного удельного сопротивления движению поезда на холостом ходу принимаем со знаком минус.
Рисунок 15.2 – Графики удельных равнодействующих сил, действующих на поезд
Режим торможения. По заданию тормозные колодки композиционные, следовательно, значения расчетного коэффициента трения тормозных колодок φкр определяем по формуле (8.10).
Прежде чем определить значения удельной тормозной силы, определим расчетный тормозной коэффициент по формуле (8.13). Значения расчетных нажатий тормозных колодок выбираем по таблице 8.2. Принимаем груженый режим для всех типов вагонов (т.к. осевая нагрузка более 6 т/ось):
Определяем удельную тормозную силу по формуле (8.11).
Удельную равнодействующую силу для режима служебного торможения определяем по формуле (8.14), а для режима экстренного торможения – по формуле (8.15). Все результаты расчетов для режима торможения сводим в таблицу 15.7. По результатам расчета строим график удельных равнодействующих сил для режима служебного торможения r тс, представленный на рисунке 15.2.
Определение предельно допустимой скорости движения при заданных тормозных средствах поезда. Прежде чем приступить к построению графика скорости, необходимо определить предельно допустимую скорость движения на участке, обусловленную тормозными возможностями поезда. Для обеспечения безопасности движения необходимо, чтобы тормозной путь поезда в режиме экстренного торможения на самом крутом спуске не превысил 1200 м.
Определим максимальную скорость движения поезда, при которой, в случае экстренного торможения, тормозной путь составит 1200 м.
Для решения этой задачи определим путь подготовки тормозов к действию S п по формуле (9.2).
Рассчитаем количество осей в составе:
Так как количество осей составляет 208, то время подготовки тормозов к действию определим по формуле (9.4). Выбираем максимальный спуск заданного участка i с = –10 ‰, для которого будет решаться тормозная задача. Расчет производится для максимальной скорости движения локомотива. В нашем случае конструкционная скорость тепловоза равна 100 км/ч.
Время подготовки тормозов к действию
Путь подготовки тормозов к действию
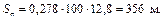
На рисунке 15.3 представлено графическое решение тормозной задачи (графическое решение тормозной задачи оформляется на листе миллиметровой бумаги формата А3 в заданном масштабе).
В результате графического решения тормозной задачи определили ограничение скорости по тормозным средствам, равное 99 км/ч (точка М пересечения кривых s п = f (v н) и v = f (s)).
Определение времени хода поезда по участку способом равновесных скоростей. Равновесную скорость на каждом элементе спрямленного профиля определяем по диаграмме удельных равнодействующих сил для режима тяги r т (см. рисунок 15.2), а время движения – по формуле (10.1).