· нажать кнопку OK.
Результаты анализа. В выходной диапазон будет выведена ковариационная матрица, в которой на пересечении каждых строки и столбца находится коэффициент ковариации между соответствующими параметрами.
Отметим, что хотя в результате будет получена треугольная матрица, ковариационная матрица симметрична, и коэффициенты ковариации sij = sji.
ПРИМЕР VIII.1
При геологическом картировании района, в строении которого принимают участие вулканогенно-осадочные породы, выделены две свиты близкого петрографического состава, но занимающие различное стратиграфическое положение. Взаимоотношение свит надежно устанавливается в отдельных «ключевых» участках; в остальной части района обнаружение пород данного состава и облика не позволяет однозначно отнести их к той или иной свите.
Предполагается, что, несмотря на свое визуальное сходство, породы данных свит несколько различаются по содержаниям отдельных породообразующих оксидов и характеру их взаимосвязи. Для установления этих отличий в ключевых участках проведено определение концентраций оксидов в отдельных пробах. В табл. VIII.1 данные опробования верхней свиты обозначены индексом A, а данные нижней свиты – индексом B.
Кроме ключевых участков определение содержаний породообразующих оксидов в сходных породах выполнено по отдельным искусственным обнажениям и скальным выходам в различных частях района, отделенных друг от друга тектоническими нарушениями, площадями с мощным покровом рыхлых отложений, в связи с чем определение их стратиграфического положения затруднено. Данные их изучения приведены в табл. VIII.2.
Требуется
На основе данных о составе свит вычислить уравнение дискриминантной функции и определить принадлежность к каждой из свит пород аналогичного состава.
Указание
Дискриминантную функцию предлагается рассчитать по сочетанию трех признаков из табл. VIII.1 (Na2O, K2O, TiO2), используя данные первых пятнадцати строк. Содержание породообразующих оксидов в сходных породах из табл. VIII.2 предлагается взять также для сочетания трех признаков (Na2O, K2O, TiO2), используя данные первой строки.
Решение
В ячейках A1, B1, C1, F1, G1 и H1 следует разместить обозначения породообразующих оксидов Na2O, K2O, TiO2 так как это показано на рис. VIII.1. Соответственно в столбцах A, B, C, F, G и H – разместить данные первых пятнадцати строк табл. VIII.1 для этих породообразующих оксидов Na2O, K2O, TiO2. В ячейках A17, B17, C17, F17, G17 и H17 следует рассчитать средние значения по каждому породообразующему оксиду. В ячейку A18 ввести формулу =СЧЁТ(A2:A16), а в ячейку F18 – формулу =СЧЁТ(F2:F16) для определения числа измерений концентраций по каждой из свит.
Таблица VIII.1 Данные анализов вулканогенно-осадочных пород верхней (А) и нижней (В) свит – содержания (в %) породообразующих оксидов
| № | Na2O | K2O | TiO2 | MgO | CaO | FeO | Na2O | K2O | TiO2 | MgO | CaO | FeO |
| A | B | |||||||||||
| 2,37 | 3,39 | 1,45 | 3,72 | 5,82 | 4,18 | 4,49 | 3,72 | 1,68 | 3,95 | 6,68 | 5,22 | |
| 4,44 | 2,64 | 1,10 | 3,14 | 4,68 | 3,56 | 4,13 | 3,55 | 1,56 | 4,38 | 6,20 | 5,60 | |
| 3,20 | 2,50 | 1,14 | 2,83 | 4,83 | 3,50 | 4,00 | 3,21 | 1,37 | 3,34 | 5,55 | 4,52 | |
| 3,71 | 3,68 | 1,22 | 4,15 | 5,62 | 3,59 | 3,48 | 2,93 | 1,22 | 3,94 | 4,72 | 3,81 | |
| 5,02 | 3,00 | 0,98 | 3,32 | 4,75 | 2,97 | 3,15 | 2,32 | 0,87 | 3,87 | 3,20 | 3,31 | |
| 4,40 | 3,47 | 0,83 | 4,06 | 4,83 | 3,00 | 2,79 | 2,28 | 0,92 | 4,18 | 3,81 | 2,62 | |
| 4,72 | 2,81 | 1,15 | 3,22 | 4,55 | 3,60 | 3,08 | 2,47 | 1,10 | 5,17 | 4,82 | 3,95 | |
| 3,81 | 3,07 | 1,09 | 3,45 | 5,31 | 3,21 | 3,37 | 2,96 | 1,15 | 4,21 | 4,31 | 3,37 | |
| 2,22 | 3,42 | 1,22 | 3,97 | 5,86 | 3,62 | 3,65 | 2,79 | 1,03 | 3,20 | 4,01 | 3,00 | |
| 3,58 | 3,05 | 1,38 | 3,49 | 5,49 | 4,02 | 3,84 | 3,34 | 1,32 | 3,92 | 5,02 | 4,51 | |
| 3,75 | 2,73 | 1,33 | 3,04 | 5,12 | 4,38 | 3,61 | 2,52 | 1,17 | 3,81 | 4,95 | 4,04 | |
| 3,84 | 3,14 | 1,48 | 3,32 | 5,30 | 4,31 | 3,96 | 2,24 | 1,45 | 4,09 | 5,92 | 5,07 | |
| 3,80 | 3,80 | 1,11 | 4,95 | 5,92 | 3,60 | 3,78 | 3,07 | 1,31 | 3,23 | 4,45 | 3,32 | |
| 3,80 | 3,15 | 1,22 | 3,73 | 5,32 | 4,00 | 3,36 | 2,49 | 0,73 | 3,80 | 3,14 | 2,27 | |
| 3,48 | 3,09 | 1,34 | 3,58 | 5,58 | 4,11 | 4,01 | 2,52 | 1,53 | 3,84 | 5,82 | 4,78 | |
| 3,42 | 3,13 | 1,45 | 3,48 | 5,43 | 4,40 | 4,40 | 4,14 | 1,82 | 2,38 | 6,92 | 4,90 | |
| 3,38 | 3,58 | 1,63 | 4,22 | 5,80 | 5,35 | 4,82 | 3,87 | 1,55 | 3,27 | 6,40 | 5,51 | |
| 3,56 | 2,67 | 1,72 | 3,12 | 5,13 | 4,50 | 4,21 | 3,42 | 1,48 | 4,00 | 6,08 | 4,63 | |
| 4,12 | 4,12 | 1,22 | 4,31 | 5,75 | 3,91 | 4,16 | 3,18 | 1,30 | 3,50 | 5,01 | 4,12 | |
| 4,58 | 3,27 | 0,75 | 3,52 | 5,40 | 3,10 | 3,17 | 3,41 | 1,52 | 4,08 | 6,12 | 4,72 | |
| 4,20 | 3,11 | 0,72 | 3,58 | 5,03 | 2,62 | 3,56 | 2,75 | 1,12 | 3,79 | 4,20 | 3,00 | |
| 4,38 | 2,16 | 0,81 | 2,38 | 4,48 | 3,30 | 2,97 | 2,16 | 0,64 | 3,38 | 2,92 | 2,93 | |
| 3,87 | 2,70 | 1,06 | 3,52 | 5,02 | 3,57 | 2,62 | 2,33 | 0,68 | 4,89 | 2,70 | 1,65 | |
| 3,28 | 3,20 | 1,10 | 3,66 | 5,61 | 3,65 | 2,37 | 1,75 | 0,85 | 4,22 | 3,10 | 3,40 | |
| 2,87 | 3,21 | 1,55 | 3,83 | 5,72 | 4,73 | 2,90 | 2,04 | 0,93 | 4,17 | 4,05 | 3,12 | |
| 2,84 | 3,39 | 1,22 | 3,72 | 5,79 | 4,21 | 3,00 | 2,61 | 1,25 | 3,52 | 5,40 | 4,65 | |
| 3,23 | 2,86 | 1,77 | 3,02 | 5,22 | 5,54 | 3,61 | 2,97 | 1,34 | 3,98 | 4,70 | 3,30 | |
| 3,72 | 3,35 | 1,14 | 4,21 | 5,39 | 4,18 | 4,12 | 3,31 | 1,50 | 3,40 | 6,03 | 5,10 | |
| 4,39 | 3,76 | 0,63 | 3,98 | 5,90 | 3,32 | 4,88 | 3,82 | 1,72 | 3,06 | 6,52 | 4,50 | |
| 3,71 | 2,92 | 0,58 | 3,01 | 5,24 | 3,38 | 4,31 | 3,22 | 1,41 | 3,38 | 5,90 | 5,30 |
Таблица VIII.2 Содержания (в %) породообразующих оксидов
| № | Na2O | K2O | TiO2 | MgO | CaO | FeO |
| 3,60 | 2,92 | 1,26 | 4,51 | 5,15 | 4,26 | |
| 3,62 | 3,10 | 1,20 | 3,12 | 4,83 | 3,75 | |
| 3,20 | 3,51 | 1,46 | 3,75 | 5,66 | 4,31 | |
| 3,98 | 3,16 | 1,38 | 3,56 | 5,60 | 4,30 | |
| 3,54 | 2,95 | 1,32 | 4,40 | 5,03 | 4,10 | |
| 3,00 | 3,71 | 1,52 | 4,21 | 6,02 | 4,72 | |
| 4,31 | 3,00 | 0,87 | 3,36 | 5,16 | 3,56 | |
| 4,43 | 3,30 | 0,73 | 3,72 | 5,21 | 3,52 | |
| 3,31 | 2,42 | 1,01 | 3,85 | 4,12 | 3,20 | |
| 3,09 | 2,27 | 0,96 | 4,53 | 3,61 | 2,01 |
Для построения ковариационной матрицы верхней свиты A в меню Сервис выберите пункт Анализ данных и далее укажите строку Ковариация. В появившемся диалоговом окне укажите Входной интервал A1:C16. Укажите, что данные рассматриваются по столбцам. Установите флажок в поле Метки в первой строке. Укажите выходной диапазон. Для этого поставьте флажок в левое поле Выходной интервал и в правое поле ввода Выходной интервал введите А20. Нажмите кнопку OK.
Для построения ковариационной матрицы верхней свиты B в меню Сервис выберите пункт Анализ данных и далее укажите строку Ковариация. В появившемся диалоговом окне укажите Входной интервал F1:H16. Укажите, что данные рассматриваются по столбцам. Установите флажок в поле Метки в первой строке. Укажите выходной диапазон. Для этого поставьте флажок в левое поле Выходной интервал и в правое поле ввода Выходной интервал введите F20. Нажмите кнопку OK.
В выходных диапазонах получаем ковариационные матрицы. Подразумевается, что в пустых клетках в правой верхней половине таблицы находятся те же коэффициенты ковариации, что и в нижней левой (симметрично расположенные относительно диагонали). Заполните пустые ячейки верхних половин таблицы так, как показано на рис. VIII.1.
Рис. VIII.1. Расчет дискриминантной функции в документе Excel
В диапазон B25:D27 введите табличную формулу {=B21:D23*A18+G21:I23*F18} для расчета выборочной матрицы.
В ячейку F25 введите формулу =A17-F17, в ячейку F26 – формулу =B17-G17, в ячейку F27 – формулу =C17-H17 для вычисления разностей оценок средних d 1, d 2 и d 3 каждого признака по форм. (VIII.3)
В диапазон I25:I27 введите табличную формулу {=МУМНОЖ(МОБР(B25:D27);F25:F27)} для расчета значений коэффициентов a 1, a 2 и a 3 по форм. (VIII.2)
Таким образом, уравнение линейной дискриминантной функции в этом случае будет иметь вид D = 0,005 x + 0,074 y – 0,073 z – по форм. (VIII.1)
Далее необходимо вычислить по форм. (VIII.6) значение функции D 0, относительно которого можно сделать вывод о принадлежности нового неизвестного объекта к тому или иному классу (свите).
В ячейку I28 введите формулу =1/2*(I25*(A17+F17)+I26*(B17+G17)+I27*(C17+H17)), результат равен 0,149.
Породы сходного облика, данные опробования которых приведены в табл. VIII.2, могут быть отнесены к верхней свите (объект класса A), если вычисленное для них значение дискриминантной функции D больше D 0, в противном случае они должны относиться к нижней свите.
В диапазоне B30:D30 (рис. VIII.1) следует разместить данные первой строки табл. VIII.2 для сочетания трех признаков (Na2O, K2O, TiO2). В ячейке I30 – ввести формулу =I25*B30+I26*C30+I27*D30. Результат равен 0,141 и, следовательно, он может быть отнесен к нижней свите (объект класса В).
ЗАДАЧА VIII.1
Требуется
Используя условия предыдущего ПРИМЕРА VIII.1, рассчитать по форм. (VIII.5) и (VIII.6) элементы матрицы (VIII.4).
Указание
Сначала вычислите следующие данные:
Затем по форм. (VIII.5) и (VIII.6) вычислите элементы матрицы:
;
;
;
;
;
.
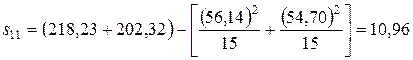В результате получите выборочную матрицу
.
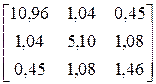ЗАДАЧА VIII.2
Дискриминантную функцию предлагается рассчитывать по сочетанию любых трех признаков из табл. VIII.1. Расчеты могут проводиться по выборкам сокращенного объема (15 – 20 значений).
ЛАБОРАТОРНАЯ РАБОТА № IX. МОДЕЛИРОВАНИЕ ПРОСТРАНСТВЕННЫХ ПЕРЕМЕННЫХ. АППРОКСИМАЦИЯ ПОВЕРХНОСТЕЙ ТРЕНДА ПОЛИНОМАМИ
При изучении строения земной коры геолога интересуют не только средние характеристики изменчивости и взаимосвязи наблюдаемых значений свойств горных пород, минеральных ассоциаций или полезных ископаемых, но также закономерности их пространственных изменений в исследуемых объемах недр. Статистические модели для этих целей непригодны, поскольку любой статистический показатель отражает лишь средний уровень изменчивости изучаемого свойства, независимо от пространственного размещения точек наблюдений, в то время, как закономерности их пространственного размещения могут оказаться принципиально различными.
К тому же, статистические характеристики обеспечивают объективные оценки уровня наблюдаемой изменчивости признака только в тех случаях, когда выборочные данные представляют собой совокупность независимых случайных величин. Для оценок реальных погрешностей изменчивости корреляционно связанных исходных данных требуется введение поправок за связь.
Для целей математического моделирования закономерностей пространственного размещения изучаемых свойств геологических образований их признаки рассматриваются не как случайные величины, а как пространственные переменные, обладающие рядом специфических характеристик: мерностью, областями существования и воздействия (определения).
Их совокупности образуют поля пространственных переменных, в пределах которых положение каждой переменной определяется координатами пространства.
Геометрические и аналитические методы моделирования геологических, геохимических, геофизических и других полей пространственных переменных способствуют объективному выделению и количественному описанию тенденций, наблюдаемых в изменении свойств исследуемых объектов, а в ряде случаев позволяют выявлять новые, ранее неизвестные закономерности. Для целей моделирования при этом используются результаты геологического картирования, геохимических и шлиховых съемок, геофизических наблюдений, геологоразведочных работ и т.д.
Пространственные закономерности изменения гранулометрического и минерального составов терригенных отложений позволяют yстановить направление сноса обломочного материала и восстановить палеогеографическую обстановку периода формирования толщ осадочных пород. По изменениям концентрации различных минералов выявляется зональность интрузивных массивов и месторождений полезных ископаемых. Пространственные закономерности изменения геофизических полей широко используются при геологическом картировании и поисках полезных ископаемых. Выявление закономерностей в изменении параметров рудных тел на ранних стадиях изучения позволяет более обоснованно оценивать не затронутые геологической разведкой фланги и глубокие горизонты месторождений, а также способствует правильному выбору размеров сети наблюдений при продолжении геологоразведочных работ. Математическое моделировавшие геохимических и геофизических полей позволяет более надежно выявлять аномалии, перспективные на обнаружение месторождений полезных ископаемых.
С помощью моделирования дискретных геологических полей устанавливаются закономерности расположения месторождений и рудопроявлений определенного генетического типа относительно интрузий, тектонических нарушений или других элементов геологического строения.
ГЕОЛОГИЧЕСКИЕ ОБЪЕКТЫ, КАК ПОЛЯ ПРОСТРАНСТВЕННЫХ ПЕРЕМЕННЫХ
Полем пространственной переменной называется область пространства, каждой точке которого поставлено в соответствие некоторое значение изучаемой переменной. В качестве геологического поля может рассматриваться область пространства, при этом каждому элементу последнего соответствует определенное значение изучаемого геологического признака.
В зависимости от природы моделируемых признаков различают геофизические, геохимические, минералогические, морфометрические и другие геологические поля, которые по размерности изучаемого пространства подразделяются на одномерные, двумерные, трехмерные и многомерные.
Непрерывные и дискретные геологические пространственные переменные. По характеру распространения (областям существования) и земной коре геологические пространственные переменные разделяются на непрерывные и дискретные.
Непрерывные пространственные переменные выражают свойства горных пород, минеральных ассоциаций или полезных ископаемых, проявленные в любой точке поля, то есть на всей площади (во всем объеме) исследуемого блока земной коры или геологического тела. К числу этих переменных относятся концентрации химических элементов в горных породах, их физические свойства, мощность изучаемых геологических тел и многие другие свойства пород и руд.
К числу дискретных пространственных переменных относятся пространственно ограниченные геологические образования, области существования (размеры) которых пренебрежимо малы по сравнению с исследуемыми площадями или объемами недр. Они представлены геологическими телами специфического состава (например, отдельными разновидностями пород), месторождениями полезных ископаемых, вкрапленниками отдельных минералов или минеральных агрегатов в породах и др.
Скалярные и векторные поля. По признакам мерности пространственных переменных различают скалярные и векторные геологические поля. Большинство обычно изучаемых геологических переменных относится к скалярным величинам, для задания которых достаточно знать их модуль и знак. Совокупности этих переменных образуют скалярные геологические поля.
Реже в геологической практике используются векторные пространственные переменные, для задания которых в каждой точке пространства необходимо знать не только модуль, но и направление переменной. Векторные случайные поля могут моделироваться как векторы, ориентированные в реальном дву- или трехмерном пространстве (например, магнитные поля) или как комплексы различных скалярных переменных (например, по содержанию нескольких химических элементов в каждой точке). Многие скалярные поля могут быть преобразованы в векторные, если изучать не исходные величины, а их производные, то есть градиенты геологических полей.
ФОН, АНОМАЛИИ И ПОВЕРХНОСТЬ ТРЕНДА
Наиболее распространенной моделью непрерывного скалярного геологического поля является модель аддитивного случайного поля, когда на плоскости с координатами x и y задаются значения непрерывной скалярной переменной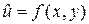 
, значения которой используются для описания аддитивного скалярного поля 
, где 
– функция координат; ε – случайная переменная.
В задачу моделирования поля входит оценка функции f (x, y)в известных предположениях относительно ε и описание случайной части ε при некоторых предположениях относительно f (x, y). Главной задачей изучения пространственных закономерностей является описание неслучайной (закономерной) компоненты поля, отражающей уровень его значений, характерный для отдельных частей изучаемой территории.
Неслучайная компонента, характеризующая основную часть моделируемого геологического поля, называется его фоном. Фоновая часть поля выявляет область относительно повышенных или пониженных значений изучаемого признака и несет в себе полезную геологическую информацию о природе изучаемого геологического объекта. Для выделения фона необходима генерализация основных свойств поля с подавлением более или менее существенных частных отклонений. В каждом конкретном случае отклонения от фона рассматриваются как аномальные.
Методы выделения фоновой части геологического поля с разделением неслучайной и случайной составляющих изучаемых признаков по эмпирическим данным получили название анализа поверхностей тренда.
В геологической практике для целей тренд-анализа используют два разных методических подхода: 1) сглаживание исходных данных скользящими статистическими окнами; 2) аппроксимация полей единой функцией пространственных координат (ортогональными полиномами и др.). Методы скользящих средних более универсальны и обеспечивают лучшие оценки средних параметров пространственно ограниченных участков геологических полей по сравнению с методам полиномиального тренд-анализа исходных данных, которые используются преимущественно для выявления региональных геологических закономерностей.
Относительный характер закономерной и случайной составляющих наблюдаемой изменчивости признаков оказывает заметное влияние на результаты тренд-анализа геологических полей. В связи с этим в зависимости от масштабов, целей, задач и условий исследований под их фонами могут подразумеваться поверхности тренда различной степени плавности, а под аномалиями – любые отклонения от фона, превышающие заданный условный уровень.
Выделение региональных закономерностей путем аппроксимации эмпирических данных функцией координат пространства связано с довольно сложными вычислениями, обычно требующими применения ЭВМ. В качестве аппроксимирующих функций используются ортогональные полиномы различных степеней, уравнение Лапласа, тригонометрические полиномы и др.
Ортогональные полиномы обычно применяются в случае равномерной прямоугольной сети наблюдений. При этом тренд определяется как линейная функция географических координат, построенная по совокупности наблюдений таким образом, что сумма квадратов отклонений значений признака от плоскости тренда минимальна. Такая модель представляет собой вариант статистического метода множественной регрессии, в котором функция 
, описывающая поверхность тренда, рассматривается как 
(где x и y – координаты пространства; β 0, β 1 и β 2 – полиномиальные коэффициенты). Для оценки трех указанных коэффициентов используются уравнения
;
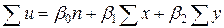; (IX.1)
;
где п – число точек наблюдения; u – значения признака в точках наблюдений; x и y – координаты точек наблюдений.
Для решения уравнений они записываются в матричной форме:
(IX.2)
и решаются относительно β 0, β 1 и β 2. Такой метод нахождения оценок биномодальных коэффициентов называется методом наименьших квадратов.
ПРИМЕР IX.1
В качестве примера рассмотрим определение плоскости тренда отметок подошвы меловых отложений, экранирующих нефтяную толщу (по Дж. Дэвису). Условные координаты площади и абсолютные отметки подошвы меловых отложений приведены в табл. IX.1.
Требуется
Произвести аппроксимацию поверхностей тренда полиномами и анализ остатков.
Таблица IX.1. Координаты скважин, абсолютные отметки подошвы меловых отложений
| № п/п | Координаты | Абс. отметка u, м | |
| x, км | y, км | ||
| –665 | |||
| –613 | |||
| –586 | |||
| –440 | |||
| –544 | |||
| –343 | |||
| –455 | |||
| –437 | |||
| –354 | |||
| –142 |
Решение
В ячейку A1 ввести обозначение x, в ячейку B1 ввести обозначение x ^2, в ячейку C1 – обозначение y, в ячейку D1 – обозначение y ^2, в ячейку E1 – обозначение x * y, в ячейку F1 – обозначение u, в ячейку G1 – обозначение x * u, в ячейку H1 – обозначение y * u. Диапазон A2:A11 заполнить значениями координат скважин x из табл. IX.1, диапазон C2:C11 заполнить значениями координат скважин y из табл. IX.1, диапазон F2:F11 заполнить значениями абсолютных отметок подошвы меловых отложений u из табл. IX.1. В диапазоне B2:B11 рассчитать соответствующие квадраты координат скважин x, в диапазоне D2:D11 рассчитать соответствующие квадраты координат скважин y, в диапазоне E2:E11 рассчитать соответствующие произведения координат x и y, в диапазоне G2:G11 рассчитать соответствующие произведения координаты x и значения абсолютных отметок подошвы меловых отложений u, в диапазоне H2:H11 рассчитать соответствующие произведения координаты y и значения абсолютных отметок подошвы меловых отложений u. В строке 12, используя кнопку Автосумма на панели инструментов Стандартная, рассчитать суммы по столбцам =СУММ(A2:A11) – Σ x, =СУММ(B2:B11) – Σ x 2, =СУММ(C2:C11) – Σ y, =СУММ(D2:D11) – Σ y 2, =СУММ(E2:E11) – Σ(x * y), =СУММ(F2:F11) – Σ u, =СУММ(G2:G11) – Σ(x * u), =СУММ(H2:H11) – Σ(y * u). В ячейке A13 рассчитать по формуле =СЧЁТ(A2:A11) число точек наблюдения n. Таким образом, для построения плоскости тренда вычисляются: