Учебно-методическое пособие
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Казанский государственный технологический университет»
Нижнекамский химико-технологический институт
Е.М. Галимова,
В.П. Дорожкин, Р.С.Ильясов
Физика и химия
высокомолекулярных соединений
Учебно-методическое пособие
Казань 2010
 |
УДК 541.64
Г 15
Физика и химия высокомолекулярных соединений: Учебно-методическое пособие / к.т.н., ст.преп. Е.М. Галимова, д.х.н., проф.В.П.Дорожкин, к.т.н., и.о.доцента Р.С.Ильясов. - Нижнекамск: Изд-во Нижнекамского химико-технол. инс-та, 2010. - 96 с.
Тематикой лабораторных работ охвачены основные разделы курсов физики и химии высокомолекулярных соединений. Содержатся методики проведения работ, порядок обработки и оформления результатов экспериментов по изучению физики и химии высокомолекулярных соединений.
Предназначены для студентов специальностей «Химическая технология высокомолекулярных соединений» и «Технология переработки пластических масс и эластомеров».
Подготовлено на кафедре химической технологии Нижнекамского химико-технологического института КГТУ.
Печатается по решению редакционно-издательского совета
Нижнекамского химико-технологического института.
Рецензенты: к.х.н., доцент Сафиуллина Т.Р.
д.т.н., проф. Петухов А.А.
 |
© Галимова Е.М., Дорожкин В.П., Ильясов Р.С.2010
© Нижнекамский химико-технологический институт (филиал) ГУО ВПО Казанский государственный технологический университет, 2010.
Лабораторная работа № 1
Изучение механо–деформационных свойств
Сшитых эластомеров
Цель работы. В результате проведения данной лабораторной работы студент должен:
1) установить основные отличия механического поведения сетчатых эластомеров от механического поведения гуковских тел в условиях одноосного растяжения;
2) определить, как влияет степень сшивания эластомера на его механическое поведение при одноосном растяжении;
3) рассчитать модуль упругости и молекулярную массу отрезка макроцепи между двумя соседними узлами сшивки образцов сшитых эластомеров;
4) определить, какому из двух уравнений (классическому уравнению высокоэластической деформации сетчатых эластомеров или эмпирическому уравнению Муни–Ривлина) лучше соответствуют полученные экспериментальные данные по одноосному растяжению сетчатого эластомера.
Краткая теория
При рассмотрении типичной зависимости величины условного напряжения (s усл.) в сетчатом эластомере от величины его относительной деформации одноосного растяжения (кривая 2 на рис. 1), то в сравнении с одноосной деформацией гуковского материала (кривая 1 на рис. 1), например, стальной проволоки, можно обнаружить следующие различия. Во-первых, зависимость (s усл. – e) для гуковского материала описывается прямой во всем диапазоне деформаций, а для сетчатого эластомера только в небольшой начальный период. Во-вторых, зависимость (s усл. – e)имеет немонотонный характер и ее вид существенно зависит от величины деформации. В-третьих, величина деформации сетчатого эластомера во много раз больше, чем у тела Гука при одной и той же величине s усл .
 |
Рис. 1. Зависимость sусл от e для различных материалов:
1 – тело Гука; 2 – сетчатый эластомер
Таким образом, если механическое поведение тела Гука хорошо описывается уравнением s усл. = E × e, где E – модуль Юнга, то для сетчатого эластомера уравнение Гука можно записать только формально: s усл. = E эфф. × e, где E эфф. – эффективный модуль резины, величина которого зависит от величины e. Для расчетов величин деформации резиновых изделий в зависимости от приложенного напряжения, и наоборот, использование уравнения s усл. = E эфф. × e крайне неудобно, так как для определенного значения s усл. (e) для данной марки резины необходимо знать конкретное значение E эфф . Именно по этой причине в 40-х годах было выведено уравнение высокоэластической деформации резины одноосной деформации растяжения, в котором фигурирует постоянный коэффициент, называемый модулем упругости резины
, (1)
где 
– степень деформации (l –длина рабочего участка образца при каком-либо значении s усл, l 0 – начальная длина рабочего участка до растяжения образца).
Так как 
, а объем резины при деформировании мало меняется (V = V 0 ; S × l = S 0 × l 0 , S 0 и S – начальная и текущая площадь поперечного сечения образца), то l = e + 1.
Одним из фундаментальных положений классической теории высокоэластической деформации сетчатых полимеров является предположение о преобладающем вкладе энтропийной составляющей изменения термодинамического потенциала при деформации по сравнению с энтальпийной. Это положение хорошо выполняется для тех сетчатых эластомеров, деформация которых обусловлена в первую очередь разворачиванием клубков макромолекул в направлении деформирования (сегментальным движением). Как правило, такими сетчатыми эластомерами являются неполярные каучуки (полиизопрен, полибутадиен) с такой степенью сшивания, при которой молекулярная масса отрезка макроцепи между двумя соседними сшивками (MC) значительно превышает величину кинетического сегмента (MC ³ 5×103 г/моль). Согласно классической теории модуль упругости резины равен
, (2)
где R = 8,31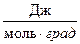 
– универсальная газовая постоянная;
T – температура в градусах Кельвина;
r – плотность резины, 
.
Классическая теория высокоэластической деформации хорошо описывает экспериментальную кривую (s – l) в пределах l £ 2. Отклонения экспериментальных данных от теоретических объясняются тем, что некоторые исходные положения теории не очень хорошо отражают реальную ситуацию. Так, предположение, что MC одинакова по объему сетки, не имеет места в реальных резинах. Далее, некоторые макромолекулы имеют циклические участки, захлесты, которые не активны для восприятия приложенной нагрузки. В теории не учитывается заторможенность внутримолекулярного вращения, неравновесность деформации, неизотермичность процесса деформирования, наличие вязкотекучей составляющей деформации, появляющейся из-за того, что часть макромолекул не вошла в сетку.
Впоследствии многие ученые получили другие, более точные зависимости s усл. , учитывающие те или иные недостатки классической теории. Известны уравнения Бартенева, Присса и других.
Тем не менее, наибольшее распространение получило эмпирическое уравнение Муни–Ривлина:
, (3)
где с 1 и с 2 – константы, характерные для каждой марки резины.
Уравнение (3) можно несколько преобразовать:
. (4)
Анализ уравнения (3) и его сравнение с классическим уравнением показывает, что при c2 = 0 2 с 1 = E. Следовательно, константа с 2 характеризует меру отклонения механического поведения реально сшитого эластомера от предсказанного классической теорией.
Многими работами показано, что уравнение Муни–Ривлина хорошо описывает экспериментальные данные до
l = 4¸5, особенно для ненаполненных резин.
Методика эксперимента
В этом разделе лабораторной работы студент должен привести следующие экспериментальные и расчетные данные.
1. Описать химический состав исходного каучука (каучуков) и привести рецептуру вулканизации резиновой смеси (смесей).
2. Описать условия деформирования резин и оборудование, на котором получена зависимость (s усл.- e).
3. По экспериментальным данным построить график зависимости s усл.- e, для образцов сетчатого эластомера, отличающихся степенью сшивания.
4. По экспериментальным данным построить график в координатах классического уравнения 
.
5. По экспериментальным данным построить график (графики) в координатах уравнения Муни–Ривлина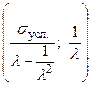 
.
Обсуждение полученных результатов
В данном разделе лабораторной работы студент должен качественно проанализировать вид полученных кривых в координатах (s усл.– e).
Рис.2. Зависимость напряжения от деформации для вулканизатов с различным содержанием вулканизующего агента
В результате анализа полученных кривых необходимо выделить на них характерные участки по диапазону деформаций. Кроме того, студент должен проанализировать влияние степени сшивания эластомера исходя из зависимости (s усл.– e)(для экспериментов ему предоставляются резины на основе одного и того же каучука, но сшитые разным количеством серы). Анализ экспериментальных данных в координатах классического уравнения должен привести к определению величины прямолинейного участка (рис. 3) и расчету верхней границы его применимости по степени растяжения l.
По величине угла наклона 
найденного прямолинейного участка студент должен определить значение E и рассчитать по уравнению (2) МС исследуемых резин.
Рис. 3. Механо-деформационная характеристика резины в координатах классического уравнения высокоэластической деформации
Такой же анализ необходимо проделать для экспериментальных данных, обработанных в координатах уравнения Муни–Ривлина (рис. 4).
Отрезок, отсекаемый на оси ординат продолжением прямой, численно равен 2 c 1. По тангенсу угла наклона (Δ у /Δ х) прямолинейного участка определяем величину 2 c 2. При 2 c 2= 0 2 c 1= Е.
Как и в случае рис. 3, необходимо на рис. 4 установить конец прямолинейной зависимости и определить значение l, до которой уравнение Муни–Ривлина хорошо описывает экспериментальные данные.
Затем следует сопоставить значения наибольших степеней деформации, до которой экспериментальные данные хорошо описываются классическим уравнением и уравнением Муни–Ривлина.
Рис. 4. Механо-деформационная характеристика резины в координатах уравнения Муни-Ривлина
Кроме того студенту, следует установить влияние количества сшивающего агента на величины модулей упругости и рассчитанные по ним значения MC.
Студентам предлагается также произвести расчеты еще одной характеристики сетчатых эластомеров: среднего числа сшивок на одну макромолекулу 
, где 
– среднечисленная молекулярная масса сшиваемого в единую пространственную сетку эластомера. Для синтетического изопренового каучука СКИ-3 можно принять равной 300×103 г/моль. После нахождения γс студент должен рассчитать сколько узлов сшивок приходится в среднем на 100 звеньев макромолекулы. Для среднесшитых резин эта цифра составляет 1–2 узла сшивания на 100 звеньев макромолекулы.
Выводы
Это заключительная часть лабораторной работы, назначением которой является лаконичное перечисление основных итогов раздела «Обсуждение результатов экспериментов». Каждый сделанный вывод должен представлять собой логично звучащее предложение, сделанное на основании проделанного обсуждения экспериментальных данных. По возможности выводы должны охватывать все полученные экспериментально расчетные результаты.
Пример вывода: Увеличение сшивающего агента серы в составе резиновой смеси на основе СКИ–3 с 0,5 масс. част. до 1,0 масс. част. приводит к возрастанию модуля упругости в 1,5 раза и соответственному росту густоты пространственной сетки.
Сделанные выводы завершают оформленную лабораторную работу.
Вопросы для самоподготовки и самоконтроля
1. Перечислите основные положения статистической теории высокоэластической деформации сшитых эластомеров.
2. Напишите итоговое уравнение теории высокоэластической деформации сшитых эластомеров, связывающее величину условного напряжения s усл. со степенью деформации l одноосного растяжения.
3. Почему деформация резины на основе полярных каучуков хуже описывается классическим уравнением высокоэластической деформации, чем деформация резин на основе неполярных каучуков?
4. Увеличивается или уменьшается модуль упругости резин E с увеличением степени их сшивания? Почему?
5. Объясните экспериментальный факт уменьшения степени растяжения полоски резины, находящейся под действием прикрепленного к ней постоянного груза, при ее нагревании.
6. Напишите эмпирическое уравнение Муни–Ривлина, связывающее s усл. резин со степенью их деформации l.
7. Объясните, как найти на основе экспериментальных данных по s усл. и l константу 2 с 1 уравнения Муни–Ривлина.
8. Объясните физическую сущность константы 2 с 1.
9. О чем свидетельствует величина константы 2 с 2?
10. Как найти из экспериментальных данных по s усл. и l модуль упругости резины E, используя классическое уравнение высокоэластической деформации?
11. Как рассчитать величину молекулярной массы отрезка макроцепи между двумя соседними узлами сшивки, зная модуль упругости резины E?
Литература
1. Кулезнев, В.Н. Физика и химия полимеров / В.Н. Кулезнев, В.А.Шершнев. – М.: Высшая школа, 1988. – 313 с.
2. Тугов, И.И.Химия и физика полимеров /И.И. Тугов, Г. И. Кострыкина. – М.: Химия, 1989. – 431с.
3.Гуль, В.Е. Структура и механические свойства полимеров / В.Е. Гуль, В.Н. Кулезнев. – М.: Высшая школа, 1979. – 351с.
Лабораторная работа № 2
Изучение ползучести, восстанавливаемости и гистерезиса сетчатых полимеров
Цель работы. Ознакомление студентов специальностей направления «Химия и технология высокомолекулярных соединений» с такими релаксационными явлениями в полимерах, как ползучесть, восстанавливаемость и гистерезис. Изучение влияния степени сшивания эластомера на данные виды релаксации.
Краткая теория
Одной из отличительных черт полимеров от других материалов является четко выраженная релаксация многих свойств во времени. Особенно наглядно это видно на примере изменения механо-деформационных свойств сетчатых эластомеров во времени после приложения постоянной нагрузки (ползучесть) и ее снятия (восстанавливаемость).
В полимерах после приложения нагрузки может произойти три вида деформации: упругая, высокоэластическая и пластическая. В зависимости от физического состояния эластомера (стеклообразное, высокоэластическое, вязкотекучее), наличия в нем пространственной сетки (сшитый эластомер) или ее отсутствия (несшитый эластомер), величины и длительности приложения нагрузки вклады вышеперечисленных видов деформации в общую будут различными.
В стеклообразном состоянии конформации макромолекул под действием тепловых флуктуаций и не очень больших приложенных нагрузок мало меняются и для полимера характерна упругая деформация, предельная величина которой достигается за короткое время (секунды или доли секунд). Обычно величина упругих деформаций невелика и не превышает нескольких процентов. Если же приложить к стеклообразному полимеру значительную нагрузку, то он под ее действием может значительно деформироваться. Большая деформация (десятки процентов) в этом случае обусловлена вытягиванием макромолекул (ориентацией) вдоль направления действия нагрузки. Если такой вытянутый полимер нагреть выше температуры стеклования, то он после снятия нагрузки вернется к прежним размерам. Такое явление получило название «вынужденная эластичность ».
Гибкоцепной полимер (эластомер), находящийся в высокоэластическом состоянии, после приложения к нему постоянной растягивающей нагрузки в зависимости от наличия в нем пространственной сетки или ее отсутствия будет вести себя по разному (рис. 5).
На рисунке 5 показаны типичные кривые ползучести (до времени t') и восстановления (после времени t') для сшитого эластомера (2) и линейного эластомера (1).
 |
Рис. 5. Зависимость величины деформации e от времени t после приложения нагрузки (до времени t') и после снятия нагрузки (время t' и после):
1 – для линейного эластомера; 2 – для сшитого эластомера
В момент приложения нагрузки эластомер быстро получает начальную деформацию (e нач.), величина которой обусловлена упругой деформацией, имеющей малое время релаксации, и большей частью высокоэластической деформацией. Сшитый эластомер из-за наличия узлов сетки имеет более высокий модуль упругости E и поэтому e нач. для него при той же величине s усл. меньше, чем у несшитого эластомера. В дальнейшем во времени будет происходить возрастание величины деформации с убывающей во времени скоростью, причем для сшитого эластомера довольно быстро может наступить момент, когда достигнутая наибольшая деформация практически не будет меняться во времени. У несшитого эластомера деформация во времени будет постоянно нарастать, и если образец не освободить от нагрузки, то рано или поздно деформация достигнет разрывных значений.
Если до наступления разрыва эластомера его освободить от нагрузки, то вначале произойдет быстрое сокращение полимера на величину, близкую к e нач. , а затем во времени будет происходить медленное восстановление образца. При этом кривая деформации будет постепенно асимптотически приближаться к оси абсцисс. Для сшитого эластомера величина остаточной деформации e ост. будет небольшой или даже равна нулю. Для несшитого эластомер e ост. может быть значительной из-за необратимого перемещения макромолекул под нагрузкой. Восстановление размеров образца после снятия нагрузки связано с тем, что вытянутые под действием нагрузки макромолекулы постепенно принимают наиболее термодинамически выгодные свернутые конформации, характерные для гибкоцепных полимеров (эластомеров).
Релаксационное явление, известное под названием «гистерезис », может наблюдаться, если провести следующий режим деформации. Подвергнем образец сшитого эластомера одноосной деформации (относительная деформация растяжения равна 300–400%), а затем предоставим возможность образцу сокращаться с той же скоростью. Как в процессе растяжения, так и при сокращении будем фиксировать значение условного растяжения в резине s усл., соответствующее тому или иному значению e. Полученная зависимость (s усл. – e) такого режима будет иметь следующий вид (рис. 6):
 |
Рис. 6. Кривые напряжение–деформация
для сшитого эластомера
Из рисунка видно, что при одной и той же величине s усл. относительная деформация растяжения e раст. будет меньше относительной деформации сокращения e сокр. . Тот факт, что e сокр. > e раст. объясняется тем, что после снятия нагрузки растяжения в точке 1 макромолекулы из ориентированного в направлении растяжения состояния начнут переходить в свернутую конформацию. Процесс этот будет происходить постепенно во времени, что связано с наличием физической флуктуационной и химической сетки, препятствующих быстрому установлению равновесных свернутых конфигураций, характерных для эластомеров. Наличие остаточной деформации e ост, вызвано, как неравновесностью проведения цикла «растяжение–сокращение», так и тем, что в ходе растяжения часть макромолекул не только развернется в направлении растяжения, но и переместит свой центр тяжести относительно других макромолекул. Эти утверждения доказываются следующими экспериментами. Если провести цикл «растяжение–сокращение» с более медленной скоростью, то есть в более равновесных условиях (на рис. 6 этот цикл показан пунктирной линией), то e ост. уменьшается. Уменьшение e ост. будет наблюдаться и при более высоких температурах испытаний за счет ускорения релаксационных процессов. e ост. будет уменьшаться при переходе от несшитого эластомера к сшитому.
Энергия W, затраченная на растяжение эластомера, прямо пропорциональна площади, лежащей под кривой растяжения (рис. 6). Энергия, возвращенная эластомером при его сокращении, прямо пропорциональна площади, лежащей под кривой сокращения. Разница между этими площадями равна площади так называемой «петли гистерезиса ». Величина этой площади характеризует величину энергии D W, необратимо рассеянной в образце эластомера в ходе цикла «растяжение–сокращение». Эта энергия может расходоваться на активацию химических реакций деструкции макромолекул или поперечных связей в ходе растяжения, на необратимую перестройку надмолекулярных структур и так далее. Чем ближе условия испытаний к равновесным, тем меньше петля гистерезиса.
Количественными характеристиками гистерезиса являются:
относительный гистерезис
; (5)
Удельный гистерезис
, (6)
где V – объем образца;