Обыкновенным дифференциальным уравнением называется уравнение
F(x, y, y/, y//, …, y(n))=0,
которое связывает независимый аргумент х, неизвестную функцию у и ее производные y, y/, y//, …, y(n).
Порядком дифференциального уравнения называется максимальный порядок производной, входящей в уравнение.
Решением дифференциального уравнения называется функция y = φ(x) которая при подстановке в уравнение превращает его в верное тождество. График этой функции называется интегральной кривой.
Для дифференциального уравнения n–го порядка
y(n) = f(x, y, y/, y//, …, y(n-1))
задача Коши формулируется следующим образом: для заданных начальных условий у0 = у(х0), 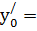 у/(х0), …,
у/(х0), …,  у(n-1)(х0) найти решение уравнения y(n) = f(x, y, y/, y//, …, y(n-1)), удовлетворяющее начальным условиям.
у(n-1)(х0) найти решение уравнения y(n) = f(x, y, y/, y//, …, y(n-1)), удовлетворяющее начальным условиям.
Функция у = ψ(х, С1, С2, …, Сn), где С1, С2, …, Сn – произвольные постоянные, называется общим решением уравнения F(x, y, y/, y//, …, y(n))=0, если выполняются два условия:
1) для любых значений С1, С2, …, Сn функция у = ψ(х, С1, С2, …, Сn) является решением дифференциального уравнения F(x, y, y/, y//, …, y(n))=0;
2) для любой точки М0(х0, у0,  ,
,  ,
,  ) (n + 1)-мерного пространства существуют такие константы
) (n + 1)-мерного пространства существуют такие константы  ,
,  , …,
, …,  , при которых график решения у = ψ(х, С1, С2, …, Сn) проходит через точку М0(х0, у0,
, при которых график решения у = ψ(х, С1, С2, …, Сn) проходит через точку М0(х0, у0,  ,
,  ,
,  ).
).
Общее решение, записанное в неявном виде, называется общим интегралом. Если в общем решении у = ψ(х, С1, С2, …, Сn) зафиксированы константы С1, С2, …, Сn, то у = ψ(х, С1, С2, …, Сn) называется частным интегралом. Решить дифференциальное уравнение – значит найти его общее решение или общий интеграл.
Дифференциальные уравнения первого порядка
Уравнения с разделяющимися переменными.
Любое дифференциальное уравнение вида φ(x) dx = ψ(y) dy называется уравнением с разделенными переменными.
Уравнение, которое приводится к виду φ(x) dx = ψ(y) dy, называется дифференциальным уравнением с разделяющимися переменными.
Пример 1. Решить дифференциальное уравнение  .
.
Решение. Уравнение является уравнением с разделяющимися переменными. Приведем его к виду φ(x) dx = ψ(y) dy:
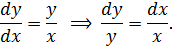
Если равны дифференциалы, то равны неопределенные интегралы  . Отсюда получаем
. Отсюда получаем  – общий интеграл и у = Сх – общее решение.
– общий интеграл и у = Сх – общее решение.
Пример 2. Решить дифференциальное уравнение (х2 – 1)у/ + 2ху2 = 0 и найти частное решение, удовлетворяющее начальному условию у(0) = 1.
Решение. (х2 – 1)dy = - 2ху2 dx 
 .
.
Таким образом, получаем общий интеграл у( ) = 1.
) = 1.
Подставляем начальное условие у(0) = 1: 1(0 + С) = 1  С = 1.
С = 1.
Отсюда получаем частный интеграл у(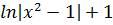 ) = 1.
) = 1.
Однородные дифференциальные уравнения первого порядка.
Функция f(x, y) называется однородной функцией m-го измерения, если f(λx, λy) =  .
.
Дифференциальное уравнение вида
P(x, y)dx + Q(x, y)dy = 0,
где P(x, y) и Q(x, y) – однородные функции одинакового измерения, называется однородным дифференциальным уравнением первого порядка.
Уравнение P(x, y)dx + Q(x, y)dy = 0 можно привести к виду у/ = f(x, y), где f(x, y) – однородная функция нулевого измерения.
С помощью замены y = ux, где u – новая неизвестная функция, уравнение P(x, y)dx + Q(x, y)dy = 0 сводится к уравнению с разделяющимися переменными.
Пример 3. 
Решение. Так как  является однородным уравнением. Сделав замену y = ux, получим
является однородным уравнением. Сделав замену y = ux, получим

Линейные уравнения первого порядка.
Линейным дифференциальным уравнением первого порядка называется уравнение вида a1(x)y/ + a0(x)y = b(x) или y/ + p(x)y = q(x).
Уравнение вида y/ + p(x)y = уnq(x), где n ≠ 0, n ≠ 1, называется уравнением Бернулли.
Для решения линейного уравнения можно применить подстановку
y = uv,
y/ = u/v + uv/,
где u и v – функции от х. Тогда уравнение y/ + p(x)y = q(x) примет вид
u/ + p(x)uv + uv/ = q(x),
u/ + (p(x)uv + uv/) = q(x),
u/ + u(p(x)v + v/) = q(x).
Если потребовать, чтобы выражение в скобках было равно нулю, т.е. p(x)v +v/ = 0, то из этого уравнения можно найти v, затем найдем u, а, следовательно, из y = uv найдем у.
Пример 4. 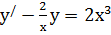 .
.
Решение. Это линейного уравнение первого порядка, где p(x) =  , q(x) =
, q(x) =  . Применяем подстановку y = uv, y/ = u/v + uv/, получаем
. Применяем подстановку y = uv, y/ = u/v + uv/, получаем
u/v + uv/ 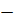
 uv =
uv =  ,
,
u/v + (uv/ 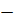
 uv) =
uv) =  ,
,
u/v + u(v/ 
 v) =
v) =  .
.
Приравниваем к нулю выражение в скобках, находим функцию v:
v/ 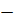
 v = 0
v = 0 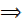 v/
v/ 
 v
v 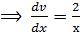 v
v 


 ln
ln  = 2ln
= 2ln 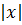
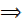 v = x2.
v = x2.
Пример 5. 
Решение. Сделав замену y = uv, y/ = u/v + uv/, получим u/v + uv/ 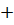
 =
= 
Сгруппируем вторе слагаемое с третьим: u/v + u(v/ 
 )=
)= 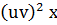 .
.
Приравнивая к нулю выражение в скобках, находим функцию v:
v/ 
 = 0
= 0 
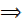 ln
ln  = 2ln
= 2ln 
 .
.
Подставив v в u/v + u(v/ 
 )=
)=  , находим u:
, находим u:
 .
.
Отсюда  .
.