Задача К1. Определение скорости и ускорения точки по заданным уравнениям ее движения.
Точка М движется в плоскости xy (рис. 18). Закон движения точки задан уравнениями x=f1(t), y=f2y(t), где x, y – в сантиметрах, t – в секундах (табл. 3, рис. 18).Найти уравнение траектории и изобразить эту траекторию на чертеже; определить в момент времени t=t1 скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны траектории. Все векторы изобразить на чертеже в масштабе.
Таблица 3 – Данные к задаче К1
| Номер варианта данных | x = f1(t), см | t = t1, c |
| 3-2t2 | ||
| 10t2 | ||
| 4t2-5 | ||
| 10-t2 | ||
| t2-4 | ||
| 2t3 | ||
| 5t2 | ||
| 4t2+1 | ||
| 3t2+2 | 
| |
| 3t2 |
|
Рисунок 18 – К задаче К1
Задача К2. Определение скоростей и ускорений точек твёрдого тела при поступательном и вращательном движениях.
По заданному уравнению прямолинейного поступательного движения груза 1 определить в момент времени t=t1 скорость и ускорение точки М и изобразить все векторы на чертеже в масштабе (табл. 4, рис. 19, 20)
Таблица 4 – Данные к задаче К2
| Номер варианта данных | Радиусы колес, см. | Уравнение движения груза 1 x=x(t), см. | t=t1 , с | ||
| R2 | r2 | R3 | |||
| 100t2+10 | 0,1 | ||||
| 12t+4t2 | |||||
| 80t2 | 0,25 | ||||
| 8t+2t2 | |||||
| 25t2 | 0,1 | ||||
| 5t+30t2 | 0,5 | ||||
| 7+40t2 | 0,2 | ||||
| 60t2+5t | 1/3 | ||||
| 10t3+2t | |||||
| 2t4 | 0,5 |
 
                    0
| 
                   1
| ||||||||||||||||
                   2
| 
                    3
| ||||||||||||||||
                      4
| 
                   5
| ||||||||||||||||
                    6
| 
                      7
| ||||||||||||||||
                  8
| 
                     9
|
Рисунок 19 – К задаче К2
Задача К3. Кинематический анализ плоского механизма.
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В. Найти для заданного положения механизма скорости точек А, В, С, D, угловые скорости звеньев 2, 3, 4, ускорение точки В и угловое ускорение звена 2. Схемы механизмов помещены на рисунке 20, 21, а необходимые данные в таблице 5. Точка С находится в середине звена АВ.
Таблица 5 – Данные к задаче К3
| Номер варианта данных | Размеры, см | ω1, с-1 | ε1, с-2 | |||
| О1А | АВ | СD | DO2 | |||
| 
|
Рисунок 20 – К задаче К3
|  
| ||
| 
| ||
|      
|
Рисунок 21 – К задаче К3
  
| 
|
Рисунок 22 – К задаче К3
Задача К4. Определение абсолютной скорости и абсолютного ускорения точки.
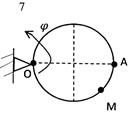
Прямоугольная пластина со сторонами a=40см, b=30 см или круглая пластина радиуса R=20 см вращается вокруг неподвижной оси по закону φ=ƒ1(t). По пластине движется точка М по закону S=AM=ƒ2(t). Найти в момент t1=1c абсолютную скорость и абсолютное ускорение точки М. Все векторы изобразить на чертеже (табл. 6, рис. 23).
Таблица 6 – Данные к задаче К4
| Номер варианта данных | φ=ƒ1(t), рад | S=AM=ƒ2(t), см | |
| Рис. 0-5 | Рис. 6-9 | ||
| 4t2-t | 5t2+20t |  R(4t2-2)
| |
| 6t2 | 20(t-t2)+15 |  Rt2
| |
| 3t-t2 | 5(3t2+2) | R(4t2-3)
| |
| 6t2-3t3 | 10t2+10 |  R(2t2-1)
| |
| 2t+t2 | 6(3t+2t2) | R(3t2-1)
| |
| 5t-6t2 | 4t+16t2 | R(4t2-2)
| |
| 3t2-2t3 | 2t2+18 | R(3t2-2t)
| |
| 5t2+t | t2+10 | R(2t2-t)
| |
| 2t-t3 | 2t2+202 | R(3t2-t)
| |
| 4t2+t | t2+15 | R(3t2-2t)
|
|
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
|
Рисунок 23 – к задаче К4
Методические указания к решению задач по кинематике
Кинематика точки
Для изучения движения точки применяются три способа [1]:
1) Векторный способ. Положение точки определяется её радиусом-вектором 
относительно некоторого неподвижного центра О в рассматриваемой системе отсчёта (рис. 24). При движении точки радиус-вектор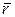 
изменяется, т.е. является векторной функцией времени:
. (13)
Уравнение (13) называется векторным уравнением движения точки. Траекторией точки является геометрическое место концов радиуса-вектора 
, построенное в выбранной системе отсчёта, т.е. годограф вектора .
Скорость и ускорение точки при заданном уравнении движения (13) равны:
Рисунок 24 – Система отчета
(14)
Вектор скорости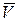 
направлен по касательной к траектории в сторону движения. Вектор ускорения 
всегда направлен в сторону вогнутости траектории точки или по её касательной (рис. 24). Векторный способ изучения движения точки обычно применяется в теоретических выкладках.
2) Координатный способ. Положение точки в выбранной, например, прямоугольной декартовой системе координат OXYZ определяется координатами:
(15)
При движении точки её координаты являются функциями времени. Выражения (15) называются уравнениями движения точки в координатной форме. Уравнение траектории точки получается из уравнений движения (15) исключением из них времени t как параметра.
Скорость и ускорение точки определяются через их проекции на оси координат:
(16)
(17)
Модуль касательного ускорения точки можно вычислить по формуле:
. (18)
Нормальное ускорение точки определяется через полное и касательное ускорения:
. (19)
Из формулы 
определяется радиус кривизны траектории:
(20)
План решения задач
1) По заданным уравнениям движения точки (как правило, на плоскости) исключением из них времени t получить уравнение траектории точки.
2) В выбранном масштабе изобразить траекторию на рисунке.
3) Определить положение точки в заданный момент времени. Для чего следует подставить этот момент в уравнения движения и вычислить координаты точки. По найденным координатам изобразить положение точки на траектории.
4) По формулам (16) – (20) для заданного момента времени определить:
– скорость точки;
– ускорение точки;
– касательное и нормальное ускорения точки;
– радиус кривизны траектории.
5) В масштабе изобразить на рисунке в ранее найденном положении точки векторы скорости, полного, касательного и нормального ускорений.
3) Естественный способ. Положение точки на заданной траектории определяется дуговой координатой S (рис. 25). Уравнение движения точки в естественной форме имеет вид:
(21)
Проекция скорости точки на направление орта касательной 
и модуль скорости определяются следующим образом:
(22)
Рисунок 25 – Положение точки на заданной траектории
Проекции ускорения на оси естественного трёхгранника, а также модуль полного ускорения определяются по формулам:
(23)
где r – радиус кривизны траектории точки.
План решения задач
1) Определить положение точки на траектории в заданный момент времени. Для этого следует подставить этот момент времени в уравнение движения (21) и вычислить дуговую координату точки. Изобразить найденное положение точки на траектории.
2) По формулам (22), (23) для заданного момента времени определить следующие величины:
– скорость точки;
– касательное, нормальное и полное ускорения точки.
3) В выбранном масштабе изобразить на рисунке в рассматриваемом положении векторы скорости, касательного, нормального и полного ускорений точки.
Пример 1. Движение точки М задано уравнениями:
, (24)
где x, y – в см,
t – в с.
Определить траекторию, скорость, полное, касательное и нормальное ускорения точки, а также радиус кривизны траектории в момент времени t= 2c.
Решение:. Находим уравнение траектории движения точки. Для этого исключаем из уравнений движения (24) время t, а именно:
.
Окончательно уравнение траектории имеет вид:
, (25)
При этом в соответствии с уравнениями движения (24) координаты точки должны удовлетворять условиям:
. (26)
На рисунке 26 изображаем траекторию в виде гиперболы, расположенной согласно условиям (26) в четвёртом квадранте.
Вычисляем координаты точки для момента времени t = 2с:
Рисунок 26 – К примеру1
см.
По найденным координатам изображаем точку на траектории (рис.26).
Далее по формулам (16) определяем скорость точки:
.
В момент времени t = 2 с:
см/с,
см/с.
Аналогично, в соответствии с формулами (17), находим полное ускорение:
при t = 2 с:
см/с2.
Определяем по формулам (18), (19) касательное и нормальное ускорения точки:
см/с2,
см/с2.
Находим радиус кривизны траектории. По формуле (1.8) имеем:
см.
Найденные векторы скорости, полного, касательного и нормального ускорений точки в выбранном масштабе показываем на рисунке 26.