Вращением твёрдого тела вокруг неподвижной оси называется такое движение, при котором хотя бы две какие-либо точки тела остаются неподвижными. Прямая, проходящая через эти неподвижные точки, называется осью вращения.
Вращение твёрдого тела вокруг неподвижной оси задаётся уравнением:
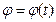, (27)
где j – угол поворота тела в рад (рис. 27).
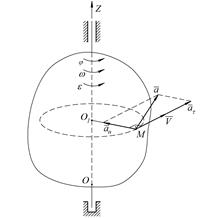
Рисунок 27 – Вращение твердого тела вокруг неподвижной оси
Алгебраические угловая скорость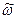 
и угловое ускорение 
тела определяются формулами:
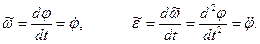(28)
Направления угловой скорости и углового ускорения определяются знаками величин 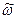и . Положительное значение соответствует положительному направлению отсчёта угла поворота j. Модули угловой скорости и углового ускорения равны:
(29)
Угловая скорость w, рад/с, и частота вращения тела n, об/мин, связаны зависимостью:
Скорость точки М тела, отстоящей от оси вращения на расстоянии О1М=h (рис. 27), вычисляется по формуле:
(30)
Ускорение этой точки равно векторной сумме касательного и нормального ускорений (рис. 27), т.е.:
.
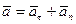Модули ускорений определяются следующим образом:
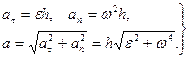(31)
При рассмотрении передаточных механизмов следует учесть, что, если два колеса находятся в зацеплении, скорость общей точки зацепления (контакта) каждого колеса одна и та же. Это же справедливо и для реечного зацепления зубчатой рейки с зубчатым колесом. В случае, когда два колеса связаны ремённой передачей скорости всех точек ремня и точек, лежащих на ободах этих колёс, также одинаковы; при этом считается, что ремень по ободу колеса не проскальзывает.
Пример 1. Груз 1 движется по закону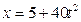 
. Определить скорость, касательное, нормальное и полное ускорения точки М механизма в момент времени, когда путь S, пройденный грузом, равен 10 см, если R2= =30см, r2 = 10 см, R3 = 20 см, r3 = 12 см (рис. 28), где x – в см, t – в с.
|
|
План решения задачи
1) Найти момент времени t 1, в который путь, пройденный грузом 1, будет равен S.
2) Определить в виде функций от времени следующие величины:
– скорость груза 1;
– угловую скорость колеса 2;
– угловую скорость и угловое ускорение колеса 3.
3) Вычислить значение угловой скорости и углового ускорения колеса 3 для момента времени t = t 1;
4) По формулам (30), (31) определить скорость, касательное, нормальное и полное ускорения точки М.
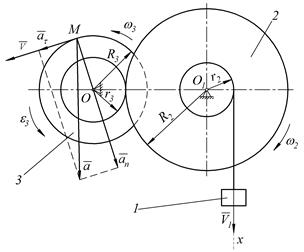
Рисунок 28 – К примеру 1.
Решение: Находим момент времени t 1, когда S = 10 см:
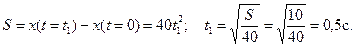
Определяем скорость груза 1:
Далее находим угловую скорость колеса 2, исходя из нерастяжимости нити и, следовательно, равенстве скорости груза 1 и точки на ободе колеса 2 радиуса r 2, т.е. 
. Тогда:
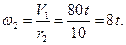
Направление угловой скорости соответствует направлению скорости груза 1 (рис. 28).
Считаем, что колёса 2 и 3 находятся в зацеплении без проскальзывания. Следовательно, скорость общей точки колёс одинакова, т.е.:
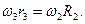
Откуда определяем угловую скорость и угловое ускорение колеса 3:
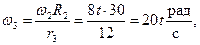
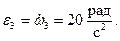
В момент времени t1 = 0,5 с:
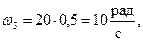
Вследствие зацепления колёс 2 и 3 направление угловой скорости 
соответствует направлению угловой скорости 
, как показано на рисунке 2.2. Угловое ускорение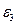 
направлено по угловой скорости , т.к. величины 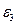и одинакового знака. По формулам (30) и (31) определяем скорость, касательное, нормальное и полное ускорения точки М:
|
|
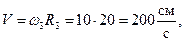
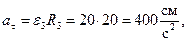
Вектор скорости направлен перпендикулярно радиусу ОМ в сторону вращения колеса 3 (рис. 28), нормальное ускорение – по радиусу к центру колеса, а касательное – перпендикулярно радиусу по направлению углового ускорения 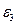.