Объектом расчета является цифровая система передачи непрерывных сообщений с импульсно-кодовой модуляцией (ЦСП с ИКМ) по каналу с шумом. Структурная схема системы приведена на рис.1 и включает в себя источник сообщений (ИС), дискретизатор (Д), кодирующее устройство (Кодер), модулятор (Мод), линия связи (ЛС), демодулятор (Дем), декодер (Дек) и фильтр-восстановитель (ФВ).
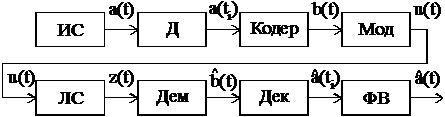
Рис.1. Структурная схема цифровой системы передачи сообщений
Из приведенной ниже таблицы необходимо выписать следующие исходные данные для расчета в соответствии с номером своего варианта, определяемого двумя последними цифрами номера студенческого билета (зачетной книжки):
интервал значений передаваемого сообщения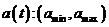 
;
полоса частот сообщения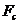 
;
номер передаваемой кодовой комбинации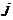 
;
вид модуляции (АМ, ЧМ, или ФМ);
спектральная плотность мощности шума 
;
способ приема (1-когерентный, 2 - некогерентный). Затем, в соответствии с приведенными далее пунктами задания, рассчитываются характеристики указанных элементов и системы в целом.
Источник сообщений
Непрерывное сообщение, поступающее от источника ИС и представленное первичным электрическим сигналом в форме напряжения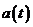 
,является стационарным случайным процессом, мгновенные значения которого распределены равномерно в интервале 
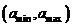, а энергетический спектр сосредоточен в полосе частот от 0до .
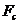Требуется выполнить следующее.
2.1.Записать аналитически и построить график одномерной плотности вероятности мгновенных значений сообщения .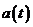
2.2.Найти соответствующую интегральную функцию распределения сообщения и построить ее график.
2.3.Рассчитать значения математического ожидания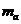 
и дисперсии 
сообщения .
|
|
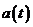Методические указания.
Необходимые теоретические сведения и формулы, касающиеся расчета вероятностных характеристик случайных сигналов, изучены в части 1 курса ТЭС и приведены в [1], п.2.5, 2.8; [2], п.2.1, 2.2; [3], п.1.1; [4], п.2.1. 2.2; а также в [5] и [6]. Конкретное числовое значение плотности вероятности сообщения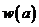 
, равномерной в заданном интервале 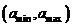, определяется из условия нормировки.
Дискретизатор
Дискретизатор преобразует сообщение в последовательность отсчетов, взятых с интервалом по времени 
. Затем каждый отсчет квантуется по уровню (напряжению) с равномерным шагом. 
.
Требуется рассчитать следующее.
3.1.Максимально допустимый интервал дискретизации .
3.2.Число уровней квантования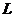 
и скорость передачи символов на выходе дискретизатора 
3.3.Среднюю мощность шума квантования.
3.4.Отношение средних мощностей сигнала и шума квантования.
3.5.Рассматривая дискретизатор, как источник дискретных сообщений с объемом алфавита 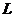, определить его энтропию 
и производительность 
при условии, что отсчеты, взятые через интервал , статистически независимы.
Методические указания.
Этот пункт задания требует для его выполнения знания теории дискретизации функций непрерывного аргумента, основных понятий теории информации. См. [1], п.2.4, 6.2, 8.9, 8.10; [2], п.2.5, 8.1; [3],п.1.3; [4], п.2.7, 4.1, 8.1, 8.2; [5].
Интервал дискретизации . определяется по теореме Котельникова. Число уровней квантования 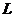рассчитывается как число шагов длиной , которое может поместиться в заданном интервале значений передаваемого сообщения .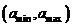
При расчете мощности шума квантования (см. указанную литературу) учитывают, что при заданном в п.2 равномерном законе распределения сообщения 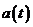все его значения, попадающие в интервал между двумя соседними уровнями квантования, равновероятны и не зависят от номера уровня. Поэтому и шум квантования 
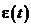(определяемый в каждый момент времени как отклонение значения исходного сообщения от ближайшего к нему уровня квантования)распределен равномерно в интервале 
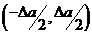. Мощности первичного сигнала (сообщения) 
и шума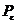 
определяются как их дисперсии.
|
|
Энтропия и производительность дискретизатора определяются по формулам расчета указанных информационных характеристик для дискретных источников, причем в роли выдаваемых ими символов здесь выступают уровни сообщения (соответственно, единицей измерения в этом случае является бит/уровень). Следует учесть, что вероятности всех уровней квантованного сообщения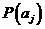 
, где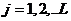 
при заданном равномерном законе распределения его мгновенных значений и выбранном способе квантования одинаковы.
Кодер
Кодер обеспечивает представление квантованных по уровню отсчетов сообщения помехоустойчивым двоичным кодом. Эта операция осуществляется в два этапа. На первом из них производится примитивное кодирование: каждый уровень квантованного сообщения 
представляется комбинацией k-разрядного равномерного двоичного кода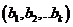 
. На втором этапе из них формируются комбинации помехоустойчивого кода.
Предполагается, что в данной системе используется широко известный код Хэмминга (7,4), исправляющий одиночные ошибки. Комбинации, принадлежащие данному коду, содержат 
информационных и 
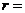3 проверочных символа. Общее число кодовых символов в одной кодовой комбинации 
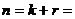7.
|
|
Кодовые символы при использовании такого кода определяются следующим образом.
Первые 4 символа совпадают с информационными:
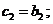
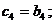(4.1}
а остальные (проверочные) символы определяются из следующих соотношений:
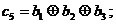
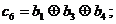
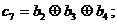(4.2)