5.1.Изобразить временные диаграммы первичного (модулирующего) сигнала 
, представляющего кодовую комбинацию 
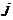- го уровня сообщения 
, как это описано в п.4, и соответствующего модулированного сигнала 
(с учетом заданного вида модуляции). Если для представления числа 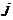используется две или более комбинаций, необходимо ограничиться комбинацией, соответствующей младшим разрядам.
5.2. Записать аналитическое выражение указанного модулированного сигнала , связывающее его с первичным сигналом .
5.3. Записать аналитическое выражение и построить график корреляционной функции первичного (модулирующего) сигнала 
.
5.4.Записать аналитическое выражение и построить диаграмму спектральной плотности мощности (энергетического спектра) этого сигнала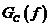 
.
5.5.Определить ширину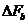 
указанного энергетического спектра 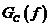как ширину главного бокового лепестка (в области положительных частот). Полученное значение 
отложить на спектральной диаграмме.
5.6.Записать аналитическое выражение и построить диаграмму энергетического спектра модулированного сигнала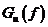 
. (Для сигналов ЧМ значение девиации частоты 
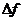выбрать таким, чтобы обеспечивалась
ортогональность элементов сигнала 
и 
на интервале 
).
5.7.Определить полосу частот (ширину энергетического спектра) модулированного сигнала 
. Отложить полученное ее значение на диаграмме спектра .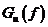
Методические указания.
Наиболее подробные сведения по этому пункту приведены в [3], глава 2, более краткие - в [2], п.1.4; [3], п.1.3, 2.2; [4], п.1.1. Для углубленной подготовки рекомендуется [1],п.3.5, 3.7.
Временные диаграммы первичного (модулирующего) сигнала и соответствующего модулированного сигнала необходимо изобразить друг под другом, с числовыми делениями по оси времени и с учетом найденного значения тактового интервала . (При изображении несущего колебания модулированного сигнала учитывать его реальную частоту 
, естественно, не требуется, достаточно условно показать два-три его периода на каждом тактовом интервале).
При записи аналитического выражения модулированного сигнала следует учесть, что это должно быть единое выражение, связывающее с первичным сигналом , а не две отдельные формулы для элементов сигнала, соответствующих символам 0 и 1, приведенные в задании.
Применительно к системе АМ величины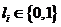 
совпадают с соответствующими кодовыми символами: 
.
Применительно к системе ЧМ значение передаваемого сигнала на заданном тактовом интервале определяется следующим соотношением:
(5.4)
где 
а сигналы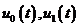 
определяются из соотношения (5.2).
Девиацию частоты 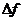следует выбрать такой, чтобы обеспечивалась ортогональность элементов сигнала 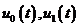на тактовом интервале .
Применительно к системе ФМ
(5.5)
Причём величины 
определяются соотношением
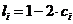(5.6)
При записи аналитического выражения корреляционной функции первичного (модулирующего) сигнала 
следует использовать (с соответствующей ссылкой на учебник) известную формулу для случайного синхронного двоичного (телеграфного) сигнала. По ней с использованием теоремы Винера-Хинчина рассчитывается соответствующий энергетический спектр .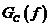
При расчете спектра модулированного сигнала 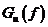также необходимо учитывать специфику двоичной модуляции. Энергетический спектр сигнала АМ получается путем сдвига спектра первичного сигнала на несущую частоту с умножением его на константу и с добавлением компоненты в виде d-функции на несущей частоте. Спектры сигналов двоичной ЧМ и ФМ легко найти, представив каждый из этих сигналов в виде суммы двух сигналов АМ с разными частотами или, соответственно, фазами. При этом складываются и их энергетические спектры (см. подробнее [5]).
При построении спектральных диаграмм следует обратить особое внимание на соответствие их масштабов для первичного и модулированного сигналов. По осям должны быть нанесены подробные числовые шкалы с учетом расчетных числовых значений всех величин.
Канал связи
Полученный в результате модуляции высокочастотный сигнал передается по каналу связи с постоянными параметрами и аддитивной помехой. Предполагается, что частотные характеристики канала выбраны таким образом, что сигнал в нем только затухает без искажений формы и временного рассеяния. С выхода такого канала на вход приемного устройства поступает смесь
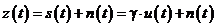(6.1)
где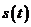 
– полезный сигнал на выходе канала, связанный с переданным сигналом известными соотношениями, 
– аддитивная помеха, приведенная к выходу канала.
Аддитивная помеха представляет собой флуктуационный гауссовский шум с равномерным энергетическим спектром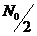 
(белый шум).
Заданы значения коэффициента передачи канала 
, (где 
– последняя цифра номера студенческого билета) и спектра шума 
(см. таблицу вариантов).