8.1.Построить проверочную матрицу кода, определённого в пункте 4.
8.2.Построить таблицу синдромов, для всех возможных вариантов одиночных ошибок. Левый столбец таблицы содержит номера ошибочных символов от 1 до7. Правый столбец таблицы должен содержать соответствующие синдромы 
, записанные в виде вектор - строк.
8.3.Вычислить в соответствии с (8.1) синдромы кодовых комбинаций, определённых в разд. 4. Ввести одиночную ошибку в одну из этих кодовых комбинаций, инвертировав символ с номером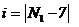 
, где 
- последняя цифра номера студенческого билета.
8.4.Определить вектор синдрома и соответствующий номер ошибочного символа. Исправить ошибку путём инвертирования ошибочного символа.
8.5.Проделать аналогичную процедуру, введя дополнительно вторую ошибку в любой из кодовых символов.
8.6.Определить вероятность необнаруженной ошибки при использовании кода Хэмминга (7,4).
8.7.Определить вероятность ошибки декодирования в режиме исправления ошибок для кода Хэмминга (7,4).
Сделать выводы.
Методические указания.
Перед выполнением этого пункта следует ознакомиться с общими принципами помехоустойчивого кодирования см. [1], глава 7; [2], п.5.3, 5.4;[3], п.5.1, 5.2;[4], п.4.2;[5], п.5.1, 5.2., [7], работа № 8.
Проверочная матрица 
может быть получена из порождающей матрицы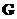 
, определяемой соотношением (4.3) следующим образом:
(8.4)
Вектор синдрома (локатора) ошибки необходимо определить как результат матричного произведения вектора принятой кодовой комбинации и транспонированной проверочной матрицы по формуле (8.3).
Вероятность необнаружения ошибки при использовании кода Хэмминга (7,4) определяется по формуле:
(8.5)
где 
- вероятность ошибки на выходе демодулятора.
|
|
Определить вероятность ошибки декодирования в режиме исправления ошибок для кода Хэмминга (7,4).
Фильтр-восстановитель
Этот элемент предназначен для восстановления непрерывного сообщения 
по принятым отсчетам 
.и представляет собой идеальный фильтр нижних частот (ФНЧ) с частотой среза 
.
Требуется выполнить следующее
9.1.Указать значение , при котором обеспечивается теоретически точное восстановление непрерывного сообщения.
9.2.Изобразить АЧХ и ФЧХ фильтра-восстановителя.
9.3.Найти его импульсную характеристику 
и начертить её график.
9.4.Записать условие физической реализуемости найденной импульсной характеристики.
Методические указания.
Выполнение этого пункта требует знания основ теории дискретизации функций непрерывного аргумента ([1], п.2.4; [2], п.2.7; [3], п.2.5; [4], п.1.3; [5], п.1.9.).
Непрерывный сигнал может быть восстановлен по своим отсчетам с помощью идеального ФНЧ, частота среза которого определяется выбранным интервалом дискретизации 
в соответствии с теоремой Котельникова.
При изображении частотных характеристик такого фильтра следует обратить особое внимание на его фазовую характеристику: идеальность ФНЧ не означает, что его ФЧХ обязательно равна нулю. Правильный вид ФЧХ указан, например, в [1], п.2.4.
Его необходимо принимать во внимание также при расчете и изображении импульсной характеристики.
Условие физической реализуемости найденной импульсной характеристики определяется фундаментальным физическим принципом причинности: реакция цепи на входное воздействие не может появиться раньше, чем воздействие появляется на входе цепи.
|
|
С учетом этого принципа следует выбрать вид импульсной характеристики и указать его связь с коэффициентом наклона ФЧХ. Аналогичные условия физической реализуемости предъявляются и к другим электрическим цепям, в частности, согласованным фильтрам (см., например, [2], стр.175). 
Литература
1. Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров. М.В. Теория электрической связи / Под ред. Д.Д. Кловского. – М.: Радио и связь, 1998.
2. Кловский Д.Д., Шилкин В.А. Теория электрической связи. – Сб. задач и упражнений. – М.: Радио и связь, 1990.
3. Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах.– М.:Связь, 1978.
4. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М.. Теория передачи сигналов /. – М.: Радио и связь, 1986.
5. Кловский Д.Д. Теория передачи сигналов.– М.: Связь, 1973.
Контакты для консультаций: