4.1.Определить число разрядов примитивного кода  , необходимое для кодирования всех
, необходимое для кодирования всех 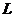 уровней квантованного сообщения.
уровней квантованного сообщения.
4.2.Записать комбинацию примитивного двоичного кода, соответствующую передаче 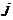 -го уровня, считая, что она представляет собой запись числа
-го уровня, считая, что она представляет собой запись числа 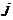 в двоичной системе счисления.
в двоичной системе счисления.
4.3.Разбить полученную последовательность на четырёхразрядные комбинации информационных символов. (При необходимости дополнить двоичное число 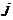 нулями в старших (левых) разрядах).
нулями в старших (левых) разрядах).
4.4. Построить порождающую матрицу используемого кода в соответствии с соотношениями (4.1) и (4.2).
4.5.Используя порождающую матрицу выразить все  =16 разрешённые кодовые комбинации через строки порождающей матрицы.
=16 разрешённые кодовые комбинации через строки порождающей матрицы.
4.6.Используя результаты п.п. 4.3. - 4.5., закодировать передаваемую информационную последовательность. При этом кодовые комбинации разделяются символами (;)
Методические указания.
Выполнение этого пункта требует знаний по разделу «Основы теории кодирования»: [1], глава 7,[2], п.5.1, 5.3, 5.4; [3], п.5.1, 5.2; [4], п.4.1, 4.2; [5]. Для более углубленного изучения этих вопросов рекомендуется.
Число разрядов примитивного кода  , необходимое для кодирования
, необходимое для кодирования 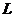 уровней квантованного сообщения, определяется из очевидного условия, что общее число всех возможных комбинаций из
уровней квантованного сообщения, определяется из очевидного условия, что общее число всех возможных комбинаций из  двоичных разрядов должно быть равно
двоичных разрядов должно быть равно 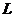 . Запись комбинации примитивного двоичного кода, соответствующей передаче
. Запись комбинации примитивного двоичного кода, соответствующей передаче 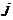 -го уровня, поясним на примере. Пусть
-го уровня, поясним на примере. Пусть  ,
,  . Представим число 217 в двоичной системе счисления:
. Представим число 217 в двоичной системе счисления:

Коэффициенты этого представления образуют 8 информационных символов комбинации примитивного кода:

| 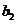
| 
| 
| 
| 
| 
| 
|
Порождающей матрицей линейного блокового  кода (где
кода (где  - общее число символов в комбинации,
- общее число символов в комбинации,  - количество информационных символов в комбинации) может служить прямоугольная матрица размера
- количество информационных символов в комбинации) может служить прямоугольная матрица размера  , строками которой являются любые
, строками которой являются любые  ненулевых линейно-независимых разрешённых кодовых комбинаций. В канонической форме строками такой матрицы являются кодовые комбинации, информационные составляющие которых образуют единичную матрицу, а проверочные символы
ненулевых линейно-независимых разрешённых кодовых комбинаций. В канонической форме строками такой матрицы являются кодовые комбинации, информационные составляющие которых образуют единичную матрицу, а проверочные символы  определяются в соответствии с соотношением (4.2):
определяются в соответствии с соотношением (4.2):
 (4.3)
(4.3)
Любую разрешённую кодовую комбинацию можно получить путём суммирования по модулю 2 двух или более строк порождающей матрицы. Нулевая комбинация, которая является необходимым элементом любого линейного кода, получается суммированием любой строки матрицы «сама с собой».
Модулятор
В этом блоке осуществляется модуляция гармонического несущего колебания  первичным сигналом
первичным сигналом 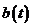 , представляющим передаваемую последовательность двоичных символов. В последующих расчетах следует принять
, представляющим передаваемую последовательность двоичных символов. В последующих расчетах следует принять  .
.
В зависимости от того, какой параметр несущего колебания изменяется в соответствии с передаваемым первичным сигналом, различают амплитудную, частотную, фазовую и другие виды модуляции. Вид модуляции выбирается в соответствии с номером варианта из таблицы. В результате модуляции двоичные символы представляются следующими высокочастотными сигналами.
Амплитудная модуляция (АМ). Символам “0” и “1” соответствуют элементы сигнала длительностью  вида
вида
 ;
;  ; (5.1)
; (5.1)
(система сигналов с пассивной паузой).
Частотная модуляция (ЧМ). Символам “0” и “1” соответствуют ортогональные элементы сигнала длительностью  вида
вида
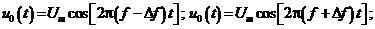 (5.2)
(5.2)
Фазовая модуляция (ФМ). Символам “0” и “1” соответствуют противофазные элементы сигнала длительностью  вида
вида
 ;
;  ; (5.3)
; (5.3)