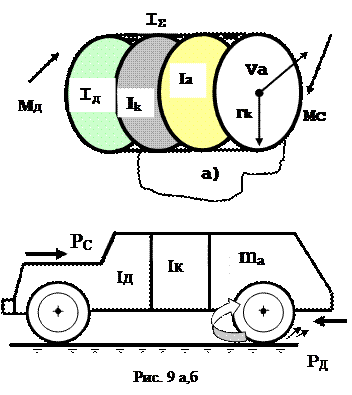
 Разгонная характеристика автомобиля – зависимость скорости и пути перемещения массы от времени Va= f(t), Sa= f(t) и по настоящее время рассматривается по упрощенной одномассовой модели, которая представляется как катящийся (вращательное движение массы) диск по плоской поверхности дороги (рис.9 а) или как движущаяся в линейном направлении по той же поверхности масса (рис.9 б). В научных исследованиях предпринимаются попытки усложнить математическую модель введением упругодемпфирующих элементов (рис. 10 а,б) между обобщённой массой маховика Iд (mд) и собственно массой автомобиля mа (Ia) как во вращательном, так и в линейном движениях. Предварительно выполненные расчёты по разгону для одномассовой модели и с упругодемпфирующими связями при сравнении полученных результатов не выявил существенных отличий выходных данных: времени, скорости и пути разгона при несоизмеримо значительном усложнении решения для модели с упругими связями. Последнее обстоятельство имеет достаточно взвешенное объяснение. С учётом современного конструирования силового привода для многих видов наземных транспортных средств, будь то автомобиль или гусеничная машина, при переходе с одной передачи на другую доля обобщенного момента инерции массы маховика двигателя резко уменьшается по сравнению с собственной массой машины или её моментом инерции. В силу свойств приведения динамической системы величины крутильных, линейных жесткостей с∑ увеличиваются также, как и коэффициенты неупругого сопротивления к∑. Такое объективное изменение параметров динамической системы «сжимает» по времени переходные процессы.
Разгонная характеристика автомобиля – зависимость скорости и пути перемещения массы от времени Va= f(t), Sa= f(t) и по настоящее время рассматривается по упрощенной одномассовой модели, которая представляется как катящийся (вращательное движение массы) диск по плоской поверхности дороги (рис.9 а) или как движущаяся в линейном направлении по той же поверхности масса (рис.9 б). В научных исследованиях предпринимаются попытки усложнить математическую модель введением упругодемпфирующих элементов (рис. 10 а,б) между обобщённой массой маховика Iд (mд) и собственно массой автомобиля mа (Ia) как во вращательном, так и в линейном движениях. Предварительно выполненные расчёты по разгону для одномассовой модели и с упругодемпфирующими связями при сравнении полученных результатов не выявил существенных отличий выходных данных: времени, скорости и пути разгона при несоизмеримо значительном усложнении решения для модели с упругими связями. Последнее обстоятельство имеет достаточно взвешенное объяснение. С учётом современного конструирования силового привода для многих видов наземных транспортных средств, будь то автомобиль или гусеничная машина, при переходе с одной передачи на другую доля обобщенного момента инерции массы маховика двигателя резко уменьшается по сравнению с собственной массой машины или её моментом инерции. В силу свойств приведения динамической системы величины крутильных, линейных жесткостей с∑ увеличиваются также, как и коэффициенты неупругого сопротивления к∑. Такое объективное изменение параметров динамической системы «сжимает» по времени переходные процессы.
В этом случае влияние переходных процессов на параметры разгона путь и скорость становится не существенным, а изменение упругого момента между массами через малый промежуток времени квазистатическим (почти постоянным).
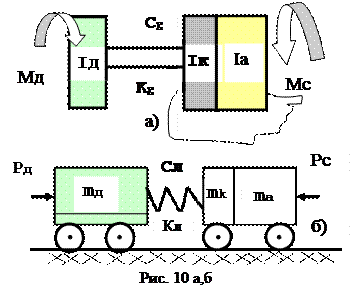 Необходимо отметить ещё одно важное обстоятельство – переходные процессы оказывают заметное влияние на динамику разгона массы на первой и второй передачах, доля которых в суммарном параметре разгона (от 5 до 10%) не является определяющей. Учитывая сказанное, остановимся на одномассовой модели разгона движущейся в линейном направлении и рассмотрим теоретические основы построения графиков 5 и 6. Движение транспортного средства по ровной дороге представляется как движение материального тела (точки). Воспользуемся фундаментальным законом движения масс под действием сил – законом Ньютона
Необходимо отметить ещё одно важное обстоятельство – переходные процессы оказывают заметное влияние на динамику разгона массы на первой и второй передачах, доля которых в суммарном параметре разгона (от 5 до 10%) не является определяющей. Учитывая сказанное, остановимся на одномассовой модели разгона движущейся в линейном направлении и рассмотрим теоретические основы построения графиков 5 и 6. Движение транспортного средства по ровной дороге представляется как движение материального тела (точки). Воспользуемся фундаментальным законом движения масс под действием сил – законом Ньютона
m∑· 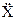 = Рд - Рс. (22)
= Рд - Рс. (22)
Разделив левую и правую части уравнения (22), получим выражение для закона изменения ускорения при движении суммарной массы m∑ под действием сил.
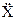 =
= 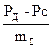 (23)
(23)
Прежде чем обратиться к алгоритму построения графиков 5 и 6 (рис. 1), уточним, из каких составляющих образуется линейная обобщенная масса m∑. Известно, что кинетическая энергия катящегося по гладкой поверхности сплошного диска (рис.9 а) является суммой двух кинетических энергий: поступательно движущейся массы m и вращательной I относительно центра оси.
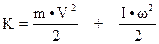
Для твёрдого тела, в нашем случае сплошного диска, связь между линейными и угловыми координатами осуществляется через радиус качения rk, т.е.
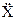 =
=  rk;
rk; 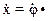 rk; x = φ· rk.
rk; x = φ· rk.
где х, φ – соответственно линейная и угловая координаты; rk – радиус качения.
При движении автомобиля в линейном направлении, как твёрдого тела, в формировании полной кинетической энергии участвует несколько масс: собственно масса автомобиля ma, моменты инерции всех опорных колёс IΣк, обобщенный момент инерции маховика двигателя Iд. Под обобщенной величиной Iд следует понимать все движущиеся детали двигателя в линейном, угловом перемещении (поршни, коленчатый вал, маховик …), включая всё навесное оборудование, приводимое в движение от силовой установки. Значительную часть величины обобщенного момента инерции маховика ДВС составляет корзина фрикционного сцепления с нажимным и ведомым дисками при однодисковом сцеплении. В двухдисковом сцеплении к величине момента инерции корзины добавляется значение промежуточного и ещё одного ведомого диска. Соблюдая равенство кинетических энергий исходной системы масс и приведённой, сведём моменты инерции всех вращающихся масс к поступательному движению (рис. 9 б), и, наоборот, движущиеся в линейном направлении массы к вращающейся суммарной массе (рис. 9 а). На рис. 9 а, б показаны составляющие суммарного момента инерции I∑ (рис.9 а) в математической модели разгона автомобиля представленной сплошным диском, а на рис. 9, б составляющие представленные в виде единой массы m∑. В абсолютно идентичных моделях (рис.9 а, б) составляющие Iд, mд – это собственная и приведённая масса маховика; Iк, mк – массы всех опорных колёс автомобиля; Ia, ma – приведённая и собственная масса автомобиля. При определении параметров разгона: пути, скорости и времени, возможно, обратиться к любой из моделей (рис. 9 а, б). В нашем случае алгоритм расчёта выполним для линейной модели (рис.9 б). В уравнении движения массы входит суммарная масса m∑, образующаяся из ряда составляющих, определение которых следует рассмотреть более подробно.
m∑ = ma + mΣк + mд (24)
Значение ma – собственно массы автомобиля определяется заданием; величина mΣк – приведенная к линейной системе суммарная масса колёс автомобиля; mд - приведенный к линейной системе обобщенный момент инерции маховика. Покажем необходимые действия для нахождения составляющих mΣк и mд. Для отыскания конкретного значения mΣк необходимо задаться типом шины, определить какая из осей имеет одинарную или двойную ошиновку и по справочникам определить массу единичной шины mш и статический радиус колеса. Существует эмпирическая зависимость, связывающая момент инерции колеса относительно оси вращения с весовыми параметрами колеса в сборе mш и геометрическим размером колеса - rст.
Iк = 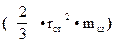 (25)
(25)
Общая величина моментов инерции всех колёс рассчитывается как I∑к = Iк ·к, где к – общее число колёс, учитывающее одинарную, двойную ошиновку. Вычислив составляющую I∑к, находим искомую составляющую m∑к.
m∑к = I∑к \ rк2. (26)
В качестве замечания отметим, что приведённая к линейному движению суммарная масса колёс m∑к отличается от действительной массы всех колёс в сборе, исчисляемой через равенство
m∑ш= mш·к кг
Соотношение собственно массы mш к приведённой массе mк рассматривается как частное от деления
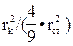
Допуская, с известной точностью, что rк ≈rст это соотношение с учётом (25) всегда равно 2,25. В исходной линейной модели разгона автомобиля имеется ещё одна составляющая mд, образующаяся от величины обобщенного момента инерции двигателя Iд. В отечественной литературе накоплен достаточный экспериментальный материал по величинам параметра Iд. Кроме опытных данных имеются эмпирические зависимости позволяющие вычислить необходимую величину обобщенного момента инерции маховика Iд на стадии проектирования. Как справочный материал в табл. 6 приведены экспериментальные значения Iд по некоторым маркам отечественных автомобилей.
Обобщенные моменты инерций маховиков двигателей некоторых
отечественных автомобилей
Таблица 6
| Марка автомобиля | ВАЗ 2101 – 2107 | Волга ГАЗ – 24 | ГАЗ – 53А | ЗИЛ – 130 | МАЗ - 500 |
| Iд, кг·м2 | 0,136 | 0,35 | 0,5 | 1,05 | 3,8 |
Для определения величины Iд расчётным путем достаточно использовать приближённую зависимость, связывающую два известных параметра: частота вращения ωN и крутящий момент двигателя Me,N при максимальной величине мощности двигателя
Iд = 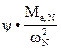 (27)
(27)
где ψ – безразмерный коэффициент. Для рядных четырёхцилиндровых высокооборотных двигателей ψ = 380…400, рядных шестицилиндровых ψ = 230…310, рядных восьмицилиндровых ψ = 370, восьмицилиндровых V – образных ψ = 210; дизельных четырёх, шестицилиндровых рядных и V – образных*) - ψ= 135…195…260*).
Определяя Iд по опытным или расчётно–приближённым значениям найденный параметр необходимо привести к линейной массе, используя выражение
mд =  (28)
(28)
Где ∑i тр,j – общее передаточное число трансмиссии на расчётной j – ой передаче. Для дальнейшего удобства расчёта полезно свести все составляющие суммарной массы в единую табл. 7, так как её величина зависит от общего передаточного числа трансмиссии.
Изменение приведённой суммарной массы по передачам Таблица 7*
| Передача | I | II | III | IV | V |
| ma, кг | |||||
| mΣк, кг | |||||
| mд, кг | |||||
| m∑, кг |
*) числовые значения приведены в качестве примера.
Достоинством введения в алгоритм разгона параметров Iд, Iк заключается в том, что имеется возможность отказаться от эмпирического коэффициента δвр – коэффициента вращающихся масс широко представленного как в отечественной, так и в зарубежной учебной и научной литературе. Величина δвр помимо достаточно грубого численного приближения «увеличения» линейной массы за счёт деталей, находящихся во вращательном движении при разгоне, не выявляет физического существа явления. Например: суммирования и перераспределения кинетической энергии по элементам механической системы связанно с учётом только квадрата передаточного коробки передач, а не всего передаточного числа трансмиссии. Численные коэффициенты δвр приводят к заметной ошибке, если применять приводимые расчётные формулы для вновь создаваемых образцов автомобильной техники. В качестве примера приведём две эмпирические зависимости для δвр опубликованных в трудах Чудакова Е.А. и Морина М.М.
δвр = 1+ δ·iк2; (δ=0,04…0,09) Чудаков Е.А.
δвр = 1+ δ·(1+iк2 ); (δ=0,03…0,05) Морин М.М.
Более правильно как с физической точки зрения, так и точности в вычислениях использовать непосредственные параметры: Iд и Iк т.е. приведённые массы моментов инерции маховика и всех опорных колёс. Однако в трансмиссии имеются и другие вращающиеся детали: шестерни коробки передач, раздаточной коробки, главной передачи, колёсных редукторов, а также полуоси и карданные валы. Величины моментов инерций этих деталей отличаются по значениям от инерционных моментов Iд и Iк на два, три порядка, следовательно, неточность расчёта параметров разгона должна иметь погрешность второго порядка, т.е. в пределах 1…2%. Напомним – инженерный расчёт допускает определение расчетных величин c точностью до 10%.