Определение допускаемых контактных напряжений

, МПа,

где σ_Нlim– предел контактной выносливости при базовом числе циклов напряжений N_H0:

для шестерни МПа;

для колеса МПа;

Z_N– коэффициент долговечности;

S_H– коэффициент запаса прочности, S_H= 1,1.

Базовое число циклов напряжений:

для шестерни ;

для колеса .

Расчетное число циклов напряжений за весь срок службы передачи при постоянном режиме нагружения

,

где n – частота вращения шестерни, колеса, мин^-1;

с – число зацеплений зуба за один оборот колеса. Для нереверсивной передачи с = 1;

L_h – срок службы передачи, ч

,

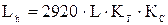где L – число лет работы передачи, L = 5 лет;

Кг – коэффициент годового использования передачи, Кг = 0,85;
Кс – число смен работы передачи в сутки, Кс = 3.

.

Расчетное число циклов напряжений:

для шестерни

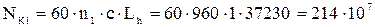; для колеса

.

Для длительно работающих передач при N_K> N_H0коэффициент долговечности равен

.

Для шестерни .

для колеса .

Допустимые контактные напряжения:

для шестерни МПа;

для колес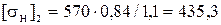а МПа.

Расчетное допускаемое контактное напряжение

МПа.

Определение допускаемых напряжений изгиба

, МПа,

где s_Flim– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений:

для шестерни МПа;

для колеса МПа;

S_F– коэффициент запаса прочности, S_F= 1,7;

Y_R– коэффициент, учитывающий влияние шероховатости переходной поверхности между зубьями, Y_R= 1;

Y_Z– коэффициент, учитывающий способ получения заготовки шестерни

и колеса. Для поковок и штамповок Y_Z= 1;

Y_А– коэффициент, учитывающий влияние двустороннего приложения нагрузки. При нереверсивной передаче Y_А= 1,0;

Y_N– коэффициент долговечности

,

где N_F0– базовое число циклов напряжений. Для сталей N_F0 = 4×10⁶.

Так как расчетное число циклов напряжений для шестерни

N_K1= 214×10⁷и для колеса N_K2= 59×10⁷больше базового числа циклов
N_F0= 4×10⁶, то принимаем Y_N= 1,0.

Допускаемые напряжения изгиба:

для шестерни

МПа;

для колеса

МПа.

Определение межосевого расстояния

, мм,

где K_a= 450 МПа^1/3– вспомогательный коэффициент;

u – передаточное число, u = 3,6;

T₁– вращающий момент на шестерне, Т₁= 75 Н×м;

K_H– коэффициент нагрузки, для прямозубой передачи предварительно принимаем К_н= 1,3;

y_{b а} – коэффициент ширины венца колеса. При симметричном расположении прямозубых колес относительно опор выбираем y_{b а} = 0,315.

мм.

Принимаем из ряда стандартных чисел (с.11) а _w= 160 мм.

Определение модуля передачи

Минимальное значение модуля из условия прочности на изгиб

, мм,

где K_m= 6,8·103 – для прямозубой передачи; b₂– ширина венца колеса

мм.

Принимаем b₂= 50 мм.

мм.

Максимально допустимый модуль передачи

мм

Принимаем по ГОСТ 9563-80 стандартное значение окружного модуля
m = 2 мм.

Определение суммарного числа зубьев шестерни и колеса

.

Определение числа зубьев шестерни и колеса

.

Принимаем z₁= 35.

Так как , то зубчатые колеса изготовляются без смещения исходного контура (.

Число зубьев колеса

.

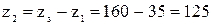Уточнение передаточного числа

.

Отклонение от заданного передаточного числа

Уточнение межосевого расстояния

.