Определение размеров зубчатых колес

Делительные диаметры:

шестерни мм;

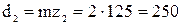колеса мм.

Диаметры вершин зубьев:

шестерни мм;

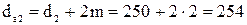колеса мм.

Диаметры впадин зубьев:

шестерни 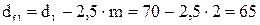мм;

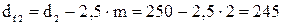колеса м.

Ширина зубчатого венца:

колеса b₂ = 50 мм;

шестерни мм.

Размеры заготовок

Диаметр заготовки шестерни

.

Для колеса с выточками:

толщина диска мм;

толщина обода заготовки колеса 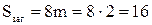мм.

Предельные размеры заготовок для стали 45:

D_пр = 80 мм; S_пр= 80 мм.

Условия пригодности заготовок выполняются, так как D_заг= D_пр, C_заг < S_пр

и S_заг < S_пр.

Определение усилий в зацеплении

Окружная сила

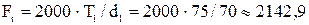Н.

Радиальная сила

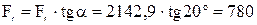Н.

Проверочный расчет передачи на контактную прочность

, МПа,

где Z_Е = 190 МПа^1/2– коэффициент, учитывающий механические свойства материалов сопряженных колес;

Z_ε – коэффициент, учитывающий суммарную длину контактных линий. Для прямозубых колес

ε_а – коэффициент торцевого перекрытия;

;

Z_H– коэффициент, учитывающий форму сопряженных поверхностей зубьев. Для прямозубых передач Z_H ≈ 2,49;

u = 3,57 – фактическое передаточное число;

K_H – коэффициент нагрузки K_H = K_HβK_Hν,

где K_Hβ– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий.

При , твердости зубьев колес ≤ 350 НВ и симметричном расположении колес относительно опор K_Hβ = 1,03;

K_Hν– коэффициент, учитывающий динамическую нагрузку.

Окружная скорость колес

м/с.

Для прямозубой передачи назначаем 8-ю степень точности изготовления.

При ν = 3,5 м/с и 8-й степени точности изготовления передачи K_Hν = 1,17.

.

Расчетное контактное напряжение

МПа;

МПа.

Отклонение расчетного напряжения от допускаемых контактных напряжений

.

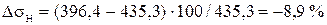Недогрузка передачи составляет 8,9 %, что допустимо.

Проверочный расчет передачи на выносливость при изгибе

, МПа,

где K_F – коэффициент нагрузки;

Y_FS– коэффициент, учитывающий форму зуба

,

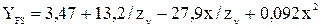z_ν– эквивалентное число зубьев колес;

х – коэффициент смещения;

Y_β – коэффициент, учитывающий наклон зуба, Y_β = 1;

Y_ε– коэффициент, учитывающий перекрытие зубьев, Y_ε= 1.

Для прямозубых передач без смещения исходного контура х₁= х₂= 0 и
zν= z.

Для шестерни ;

для колеса .

Коэффициент нагрузки ,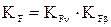

где K_Fν– коэффициент, учитывающий динамическую нагрузку. При ν = 3,5 м/с и 8-й степени точности K_Fν= 1,34;

K_Fβ– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий

.

Тогда .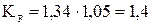

Расчетное напряжение изгиба в зубьях колеса

МПа.

Расчетное напряжение изгиба в зубьях шестерни

МПа.

Задание №1

Рассчитать цилиндрическую закрытую прямозубую передачу и выполнить чертеж зубчатого колеса. Исходные данные: вращающий момент на валу шестерни Т₁ (Н×м), частота вращения шестерни n₁(мин^-1), частота вращения колеса n₂(мин^-1), передаточное число u. Передача не реверсивная, нагрузка близка к постоянной, расположение зубчатых колес по схеме передачи (рис. 2.2.2), указанной в табл. 2.4.1.

 

Таблица 2.4.1

№ варианта	Т1	n1	n2	u	Схема передачи
				2,8
				3,55
				4,5
				3,55
				3,15
				6,3
				5,6
				4,5
				6,3
				3,15
				2,8
				4,5
				3,55
				2,8

Продолжение табл. 2.4.1

№ варианта	Т1, Н×м	n1	n2	u	Схема передачи
				3,55
				4,5
				3,55
				3,15
				6,3
				5,6
				4,5
				6,3
				3,15
				2,8
				4,5
				3,55

Контрольные вопросы для самопроверки

Каковы основные достоинства и недостатки зубчатых передач по сравнению с другими передачами?

По каким признакам классифицируют зубчатые передачи?