Закон сохранения импульса для механической системы
Механической системой называется совокупность материальных тел (точек), рассматриваемых как единое целое.
Силы взаимодействия между материальными точками внутри системы называются внутренними. Силы, с которыми на систему действуют внешние тела, называются внешними. Замкнутой (изолированной) называется система, на которую не действуют внешние силы, либо равнодействующая внешних сил равна нулю.
|
2-й закон Ньютона для i -й материальной точки:
(1)
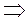
, (2)
т.е. изменение импульса механической системы равно равнодействующей внешних сил.
Для замкнутой системы (
) имеем закон сохранения импульса
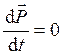
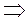
(3)
т.е. суммарный импульс замкнутой системы тел остается постоянным.
|
При поступательном движении удобно пользоваться понятием центра масс физической системы.
Центром масс системы тел называется воображаемая точка С, положение которой характеризует распределение массы системы, а ее радиус-вектор:
. (4)
Скорость центра масс
(5)
Импульс системы равен произведению массы системы на скорость ее центра масс
(6)
В соответствии с законом изменения импульса (2) имеем закон движения центра масс:
,
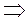
Центр масс движется как материальная точка, в которой сосредоточена масса всей системы, и на которую действует сила, равнодействующая внешних сил.
Динамические характеристики вращательного движения: момент силы, момент инерции. Определение моментов инерции тел простой формы. Теорема Штейнера. Основной закон динамики вращательного движения. Закон сохранения момента импульса
К динамическим характеристикам относятся:
· момент силы относительно точки и оси;
· момент инерции;
· момент импульса;
· импульс момента силы.
      
|
1. Моментом силы 
относительно точки О΄ называется вектор 
(псевдовектор), определяемый равенством
(1)
Правило векторного произведения: векторным произведением называется вектор, перпендикулярный плоскости двух векторов и направленный так, что из его конца кратчайший поворот от первого вектора ко второму виден против часовой стрелки.
Направление вектора может быть также определено по правилу правого винта.
Модуль этого вектора
M = F 
r 
sina. (2)
Величина b = r sina называется плечом силы (кратчайшее расстояние от точки О΄ до линии действия силы).
|
Моментом силы относительно оси ОО называется скалярная величина М 00, равная проекции на эту ось вектора 
момента силы, определенного относительно точки О΄, лежащей на данной оси.
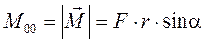. (3)
В частном случае, когда вектор силы находится в плоскости, перпендикулярной оси вращения, и действует по касательной к окружности, момент силы 
(4)
2. Момент инерции J - скалярная физическая величина, мера инертности тела во вращательном движении, зависящая от массы тела и ее распределения относительно оси вращения.
Для материальной точки тела 
, [кг×м2] (5)
Для сплошного тела 
. (6)
Моменты инерции тел простой формы
|
Теорема Штейнера
Применяется для нахождения момента инерции тела относительно произвольной оси вращения.
Момент инерции JС относительно произвольной оси равен сумме момента инерции J 0относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния d между осями:
|
. (7)
Пример. Момент инерции сплошного диска относительно оси, проходящей через точку С перпендикулярно плоскости диска
.
|
3. Моментом импульса 
материальной точки относительно точки О называется векторное произведение радиуса-вектора 
материальной точки на ее импульс 
, 
. (8)
Модуль момента импульса
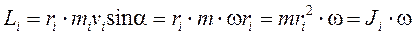
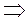
(9)
Направление вектора определяется также по правилу правого винта или по направлению вектора угловой скорости.
Для материальной точки, движущейся по окружности, модуль момента импульса
(10)
4. Импульсом момента силы 
, [Н×м×с] называется векторная величина, численно равная произведению момента силы на время ее действия и совпадающая по направлению с направлением момента силы
Уравнение моментов
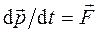
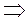
(11)