Одинаковой частоты. Биения.

 

х ₁ = А ₁ cos (w₀ t + j₁),

(1)

x ₂ = A ₂ cos (w₀ t+ j₂).

 

х = х ₁ + х ₂. (2)

, (3)

 

. (4)

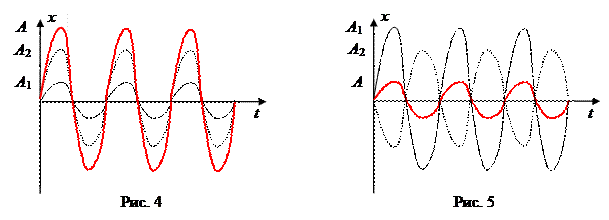
Частные случаи

1. Колебания совпадают по фазе: j₂ - j₁ = 0

А = А ₁ + А ₂ .

2. Колебания находятся в противофазе a₂ - a₁ = .

Особый интерес представляет случай, когда два складываемых гармонических колебания мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармонические колебания с пульсирующей амплитудой. Такие колебания называются биением.

 

x ₁ = A cos w t, x ₂ = A cos (w + Dw) t. Dw << w. (5)

 

(6)

 

Амплитуда и частота биений

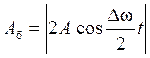, . (7)

 

 

Вынужденные колебания. Резонанс

 

Колебательная система подвергается действию внешней вынуждающей силы, изменяющейся со временем по гармоническому закону:

F_x = F ₀sinW t. (1)

 

 

Рис. 2

 

Вынужденные колебания – это незатухающие колебания. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколеба­тель­ными, а процесс незатухающих колебаний в таких системах – автоколебаниями.

 

 

Волновое движение. Уравнение плоской незатухающей бегущей волны. Энергия упругой волны. Вектор плотности потока энергии

Волновым процессом (или волной) называется процесс распространения колебаний в сплошной среде.

Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Виды волн: волны на поверхности жидкости,

Упругие,

Электромагнитные волны.

Поперечная волна Продольная волна Рис. 1

Упругими волнами называются механические возмущения, распро­стра­ня­ю­щиеся в упругой среде. Упругие волны бывают продольные и поперечные. П родольные волны – частицы колеблются в направлении распространения волны. П оперечные волны – частицы колеблются в плоскостях, перпендикулярных направлению распространения волны.

Упругая волна называется гармони­ческой, если соответствующие ей колебания частиц являются гармоническими.

Фронтом волны называется геомет­ри­чес­кое место точек, до которых доходит колебание к данному моменту времени.

Волновой поверхностью называется геометрическое место точек, колеблющихся в одинаковой фазе. Расстояние между ближайшими части­цами, колеблющимися в одина­ко­­вой фазе, называется длиной волны l (l = vT).

 

Уравнение плоской бегущей волны

 

Колебания источника

Колебания приемника

.

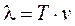
– волновое число, харак­те­ри­зующее число волн, укладыва­ющих­ся на отрезке 2p радиан.

 

– уравнение плоской бегущей волны (1)

 

– фаза волны, характеризует смещение от положения равновесия частиц, находящихся в момент времени t на расстоянии l от источника;

– временна¢я часть фазы, определяет смещение частиц в данный момент времени;

– пространственная часть фазы, определяет смещение частиц на расстоянии l от источника колебаний.

Фазовая скорость

 

 

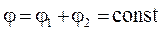
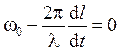
. (2)

 

Фазовой скоростью v _ф скорость перемещения фазы волны. Зависимость фазовой скорости от частоты дисперсией волн, а среда, в которой наблюдается дисперсия волн, - диспергирующей средой.

Фазовая скорость пропорциональна частоте колебаний, а поскольку для частоты ограничений не существует, не существует ограничений и для фазовой скорости: она может быть больше скорости света в вакууме.