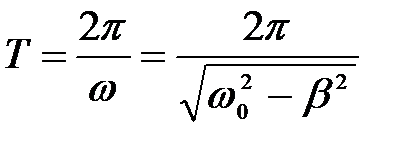Период затухающих колебаний

.

Логарифмический декремент затухания d характеризует быстроту затухания колебаний

,

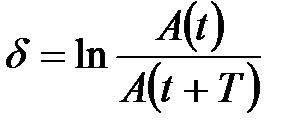где A (t) и A (t + T) – амплитуды двух соседних колебаний.

Для N полных колебаний

.

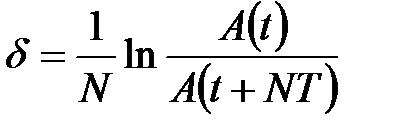Найдем связь между логарифмическим декрементом затухания и коэффициентом затухания

.

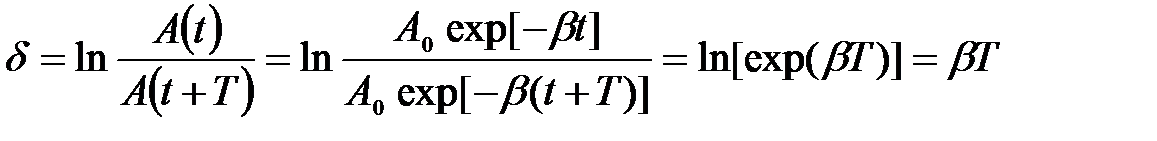Обозначим через t время, в течение которого амплитуда колебаний уменьшается в е = 2,718 раз. Тогда

,

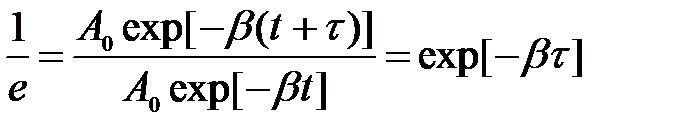следовательно, .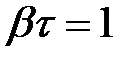

.

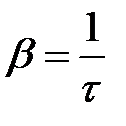Выясним физический смысл логарифмического декремента затухания.

,

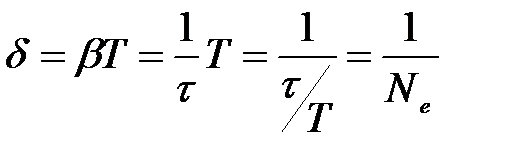где N_e – число колебаний, происходящих за время t.

.

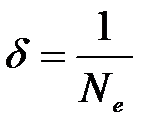13. Затухающие механические колебания. Амплитуда затухающих колебаний. Коэффициент затухания, физический смысл. Логарифмический декремент затухания, добротность, их физический смысл … затухающих колебаний.

Амплитуда затухающих колебаний зависит от времени

,

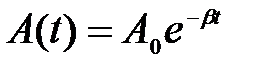здесь А ₀ – амплитуда в начальный момент времени t = 0.

Логарифмический декремент затухания – величина, являющаяся мерой снижения амплитуды колебаний за один период, натуральный логарифм отношения амплитуд 2-х последовательных колебаний.

Логарифмический декремент затухания d характеризует быстроту затухания колебаний

,

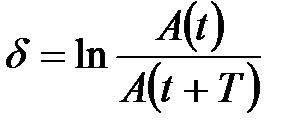где A (t) и A (t + T) – амплитуды двух соседних колебаний.

Для N полных колебаний

.

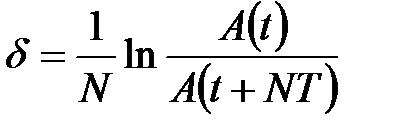Коэффициент затухания - это постепенное ослабевание собственных колебаний, обусловленное потерями энергии колебательной системой и приводящее к уменьшению амплитуды колебаний

Физический смысл коэффициента затухания b. Коэффициент затухания есть величина, обратная времени, за которое амплитуда колебаний уменьшается в e раз

.

 

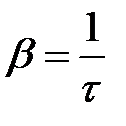Добротность колебательной системы характеризует ее способность сохранять энергию колебаний. Добротность пропорциональна отношению энергии W колебаний системы в произвольный момент времени t к убыли этой энергии за период D W

.

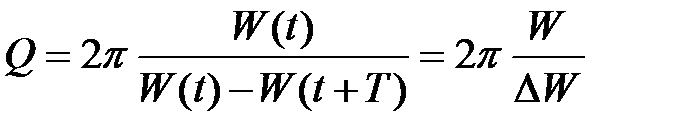Физический смысл. Добротность обратно пропорциональна логарифмическому декременту затухания или пропорциональна числу колебаний N_e, по прошествии которых амплитуда убывает в е = 2,718 раз

.

 

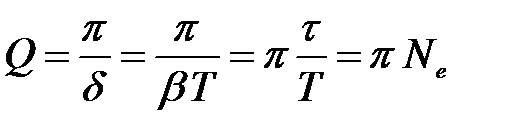Выясним физический смысл логарифмического декремента затухания.

,

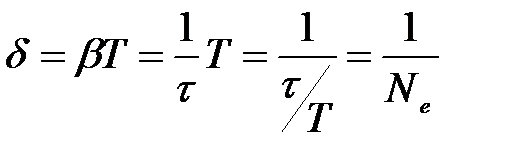где N_e – число колебаний, происходящих за время t.

Физический смысл логарифмического декремента затухания d.

Логарифмический декремент затухания есть величина, обратная числу колебаний N_e, по завершению которых амплитуда уменьшается в е = 2,718 раз

.

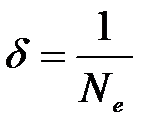14. Затухающие электромагнитные колебания в RLC-контуре. Вывод дифференциального уравнения.

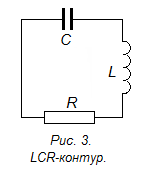Рассмотрим собственные колебания в контуре с сосредоточенными параметрами. Емкость С, индуктивность L и активное сопротивление R образуют (рис. 3) последовательный колебательный контур (RLC контур).

Будем считать, что электрические процессы в контуре квазистационарны. Это значит, что мгновенное значение силы тока i одно и то же в любом месте контура и к мгновенным значениям электрических величин можно применять правила Кирхгофа.

Согласно второму правилу Кирхгофа алгебраическая сумма напряжений в любом замкнутом контуре равна алгебраическая сумме ЭДС, в этом контуре. В нашем случае сумма напряжений на конденсаторе и на активном сопротивлении равна ЭДС самоиндукции, которая возникает за счет изменения тока в катушке при перезарядке конденсатора

,

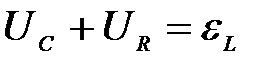где 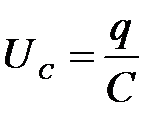– напряжение на конденсаторе,

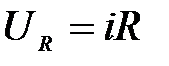– напряжение на активном сопротивлении,

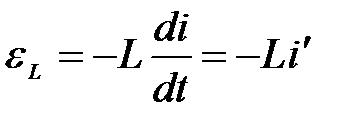– ЭДС самоиндукции в катушке.

Используем определение силы тока

.

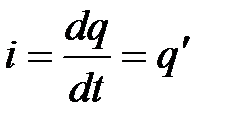Закон Кирхгофа примет вид

.

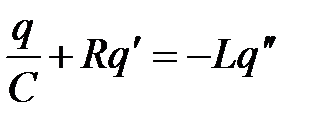Разделим обе части этого уравнения на L

.

Введем следующие обозначения

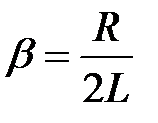– коэффициент затухания,

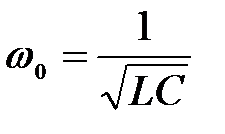– циклическая частота собственных колебаний контура.

Получили дифференциальное уравнение затухающих колебаний, описывающее изменение со временем заряда на обкладках конденсатора в RLC контуре

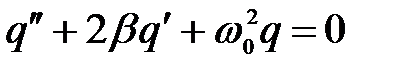(1)

Это однородное линейное дифференциальное уравнение второго порядка с обыкновенными производными и с постоянными коэффициентами.

 

15. Затухающие электромагнитные колебания в RLC-контуре. Решение дифференциального уравнения период и частота колебаний.

Рассмотрим собственные колебания в контуре с сосредоточенными параметрами. Емкость С, индуктивность L и активное сопротивление R образуют (рис. 3) последовательный колебательный контур (RLC контур).

Будем считать, что электрические процессы в контуре квазистационарны. Это значит, что мгновенное значение силы тока i одно и то же в любом месте контура и к мгновенным значениям электрических величин можно применять правила Кирхгофа.

Согласно второму правилу Кирхгофа алгебраическая сумма напряжений в любом замкнутом контуре равна алгебраическая сумме ЭДС, в этом контуре. В нашем случае сумма напряжений на конденсаторе и на активном сопротивлении равна ЭДС самоиндукции, которая возникает за счет изменения тока в катушке при перезарядке конденсатора

Дифференциальное уравнение затухающих колебаний, описывающее изменение со временем заряда на обкладках конденсатора в RLC контуре

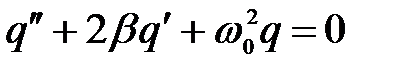(1)

Это однородное линейное дифференциальное уравнение второго порядка с обыкновенными производными и с постоянными коэффициентами. Решение этого уравнения имеет различный вид в зависимости от соотношения между коэффициентами.

1) Если w ₀ > b, то решением уравнения (1) является уравнение затухающих колебаний

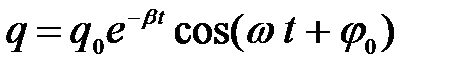, (2)

где: q ₀ – заряд конденсатора в начальный момент времени,

j ₀ – начальная фаза.

Значения q ₀ и j ₀ определяются из начальных условий.

Циклическая частота затухающих колебаний меньше собственной частоты

.

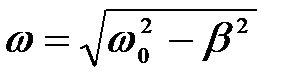Период затухающих колебаний всегда больше периода собственных колебаний

.

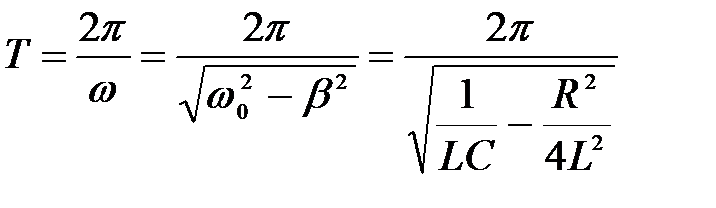Разделив (2) на электроемкость конденсатора С, получим напряжение наконденсаторе

.

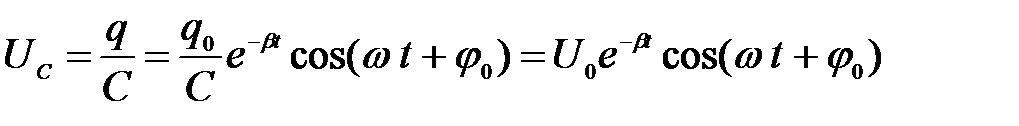Чтобы найти силу тока, продифференцируем (2) по времени

,

.

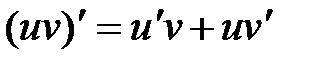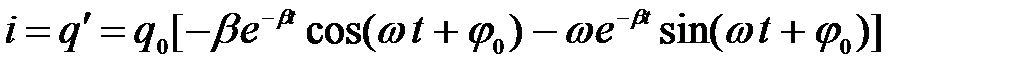Умножим и разделим это выражение на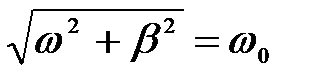

 

 

 

.

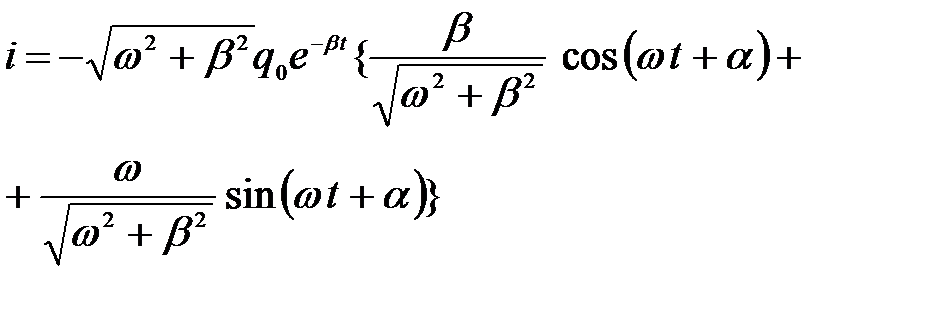
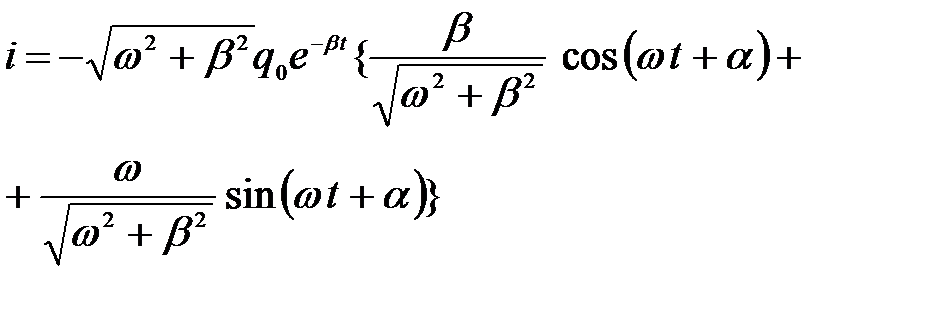
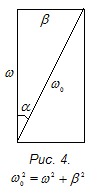Введем угол a, определяемый условиями (рис.4)

,

.

 

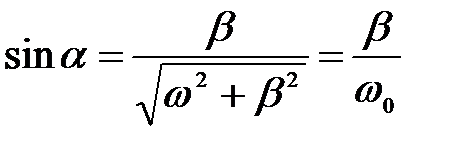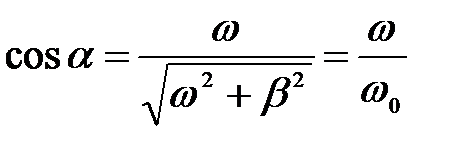Тогда можно записать

 

,

.

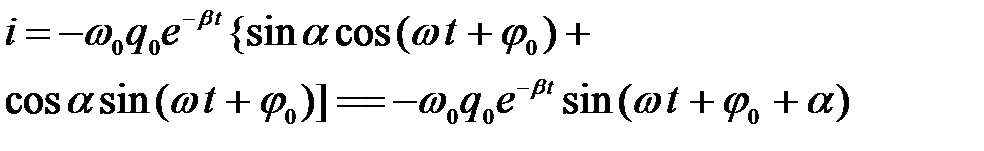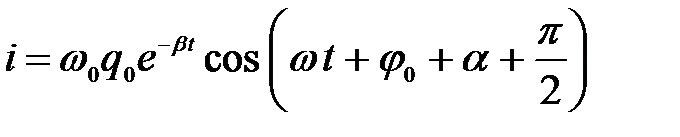Поскольку cos a > 0, а sin a > 0, то 0 < a < p /2.

Таким образом, при наличии в контуре активного сопротивления ток опережает по фазе напряжение на конденсаторе более чем на p /2 и менее чем на p (при R = 0 на p /2).

График затухающих колебаний заряда q изображен на рис. 5. Графики для напряжения и силы тока имеют аналогичный вид.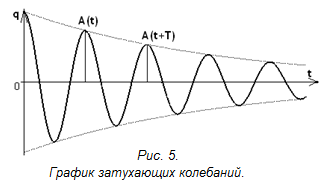

2) Пусть сопротивление контура велико, так что b > w ₀. В этом случае частота затухающих колебаний будет мнимой

,

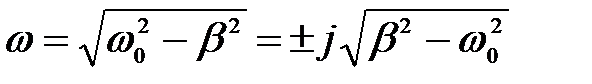где 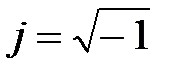– мнимая единица.

Это значит, что электрических колебаний в контуре не будет. В этом случае решение дифференциального уравнения (1) имеет вид апериодического процесса

,

, ,

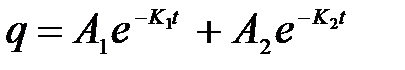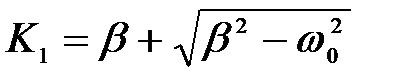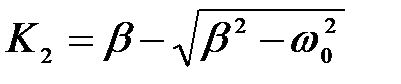где А ₁ и А ₂ постоянные, так как b > w ₀, то К ₁ и К ₂ оба вещественны и положительны.

Значения постоянных определяются начальными условиями задачи

,

.

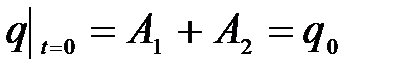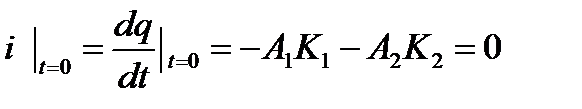Это дает , .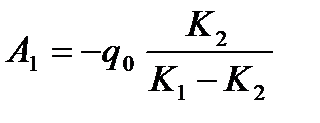

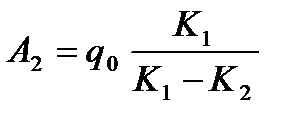После чего решение принимает вид:

.

На рис. 6 изображены графически оба слагаемых этой формулы (пунктир) и их сумма (сплошная линия). Вместо колебаний происходит апериодический разряд конденсатора. Если сопротивление контура очень велико, так что b >> w ₀, то К ₁ >> К ₂ и в последнем выражении можно пренебречь вторым слагаемым по сравнению с первым, а в знаменателе – К ₂ по сравнению с К ₁. Тогда .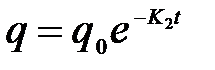

 

j

t

A 0 e–bt

16. Затухающие электромагнитные колебания в RLC-контуре. Амплитуда затухающих колебаний, коэффициент затухания. Его физический смысл. Период затухающих колебаний. Логарифмический декремент затухания, добротность, их физический смысл. Энергия затухающих колебаний.

Амплитуда затухающих колебаний зависит от времени

,

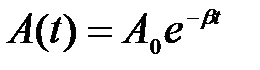здесь А ₀ – амплитуда в начальный момент времени t = 0.

 

Коэффициент затухания - это постепенное ослабевание собственных колебаний, обусловленное потерями энергии колебательной системой и приводящее к уменьшению амплитуды колебаний

Физический смысл коэффициента затухания b. Коэффициент затухания есть величина, обратная времени, за которое амплитуда колебаний уменьшается в e раз

.

 

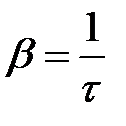Период затухающих колебаний всегда больше периода собственных колебаний

.

 

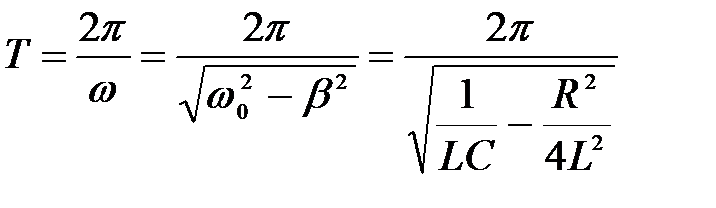Логарифмический декремент затухания – величина, являющаяся мерой снижения амплитуды колебаний за один период, натуральный логарифм отношения амплитуд 2-х последовательных колебаний.

Логарифмический декремент затухания d характеризует быстроту затухания колебаний

,

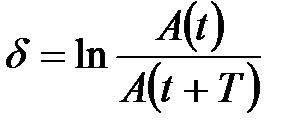где A (t) и A (t + T) – амплитуды двух соседних колебаний.

Для N полных колебаний

.

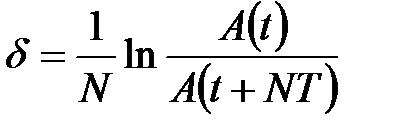Добротность колебательной системы характеризует ее способность сохранять энергию колебаний. Добротность пропорциональна отношению энергии W колебаний системы в произвольный момент времени t к убыли этой энергии за период D W

.

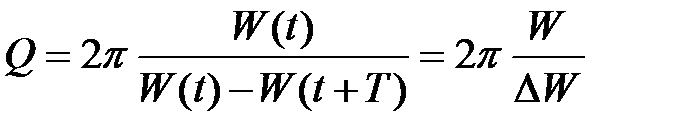Найдем связь между добротностью и логарифмическим декрементом затухания. При малых затуханиях w0 > b энергия меняется по закону

.

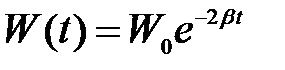Найдем изменение энергии за один период колебаний

,

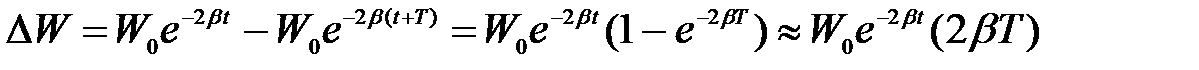т.к. 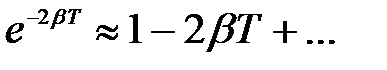, если .

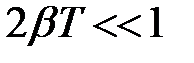Подставим в добротность и учтем что d = bТ

.

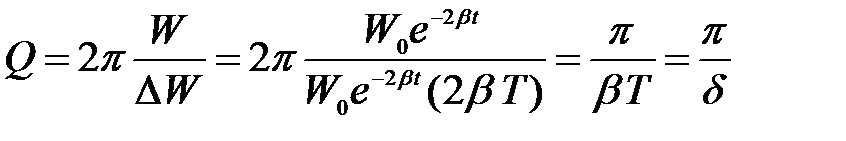Физический смысл. Добротность обратно пропорциональна логарифмическому декременту затухания или пропорциональна числу колебаний N_e, по прошествии которых амплитуда убывает в е = 2,718 раз

.

 

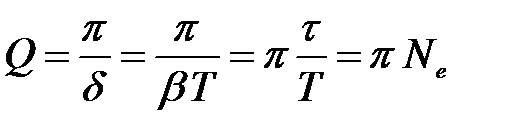Выясним физический смысл логарифмического декремента затухания.

,

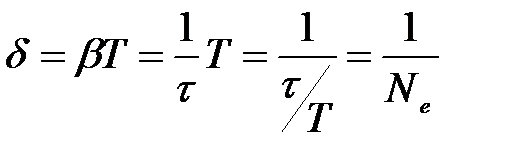где N_e – число колебаний, происходящих за время t.

Физический смысл логарифмического декремента затухания d.

Логарифмический декремент затухания есть величина, обратная числу колебаний N_e, по завершению которых амплитуда уменьшается в е = 2,718 раз

.

 

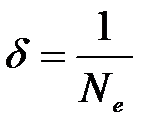17. Вынужденные механические колебания. Вывод дифференциального уравнения вынужденных колебаний.

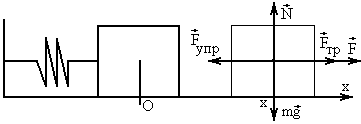
Вынужденными механическими колебаниями называются колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся ЭДС.

Помимо сил упругости и вязкого трения, на шарик действует внешняя вынуждающая периодическая сила, изменяющаяся по гармоническому закону .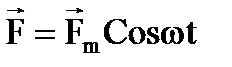

Частота, которой может отличаться от собственной частоты колебаний маятника ωo. Природа этой сил в данном случае нам не существенна. Создать такую силу можно различными способами, например, сообщить шарику электрический заряд и поместить его во внешнее переменное электрическое поле. Уравнение движения шарика в рассматриваемом случае имеет вид

По второму закону Ньютона, записанному в проекциях на ось x:

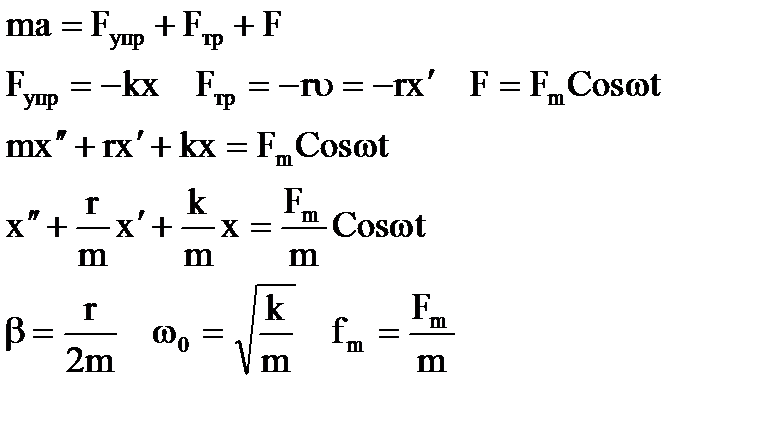
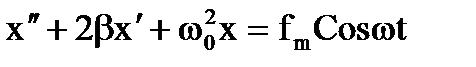- ДУ вынужденных колебаний.

 

1. Вынужденные механические колебания. Решение дифференциального уравнения. Резонанса.

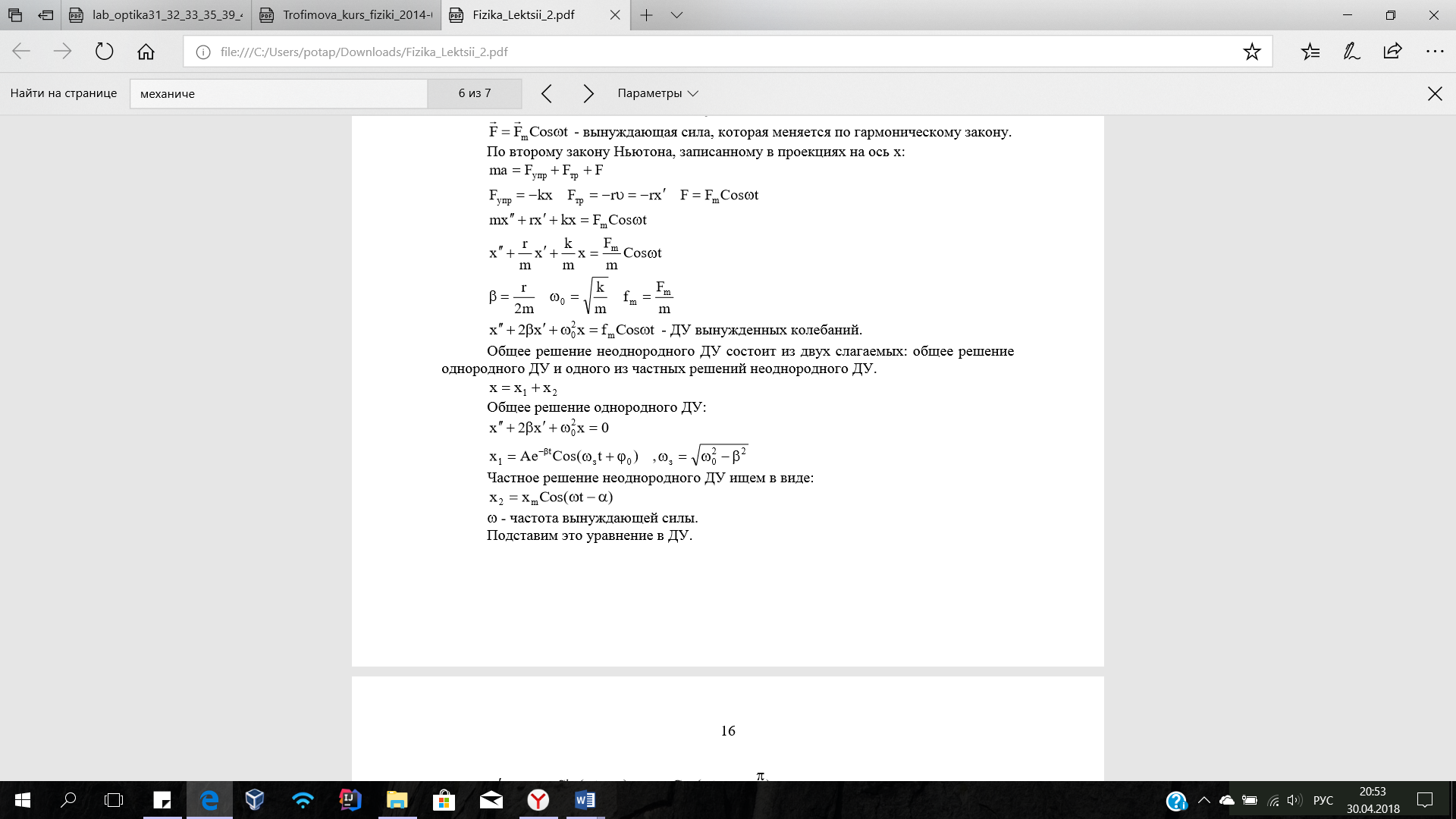
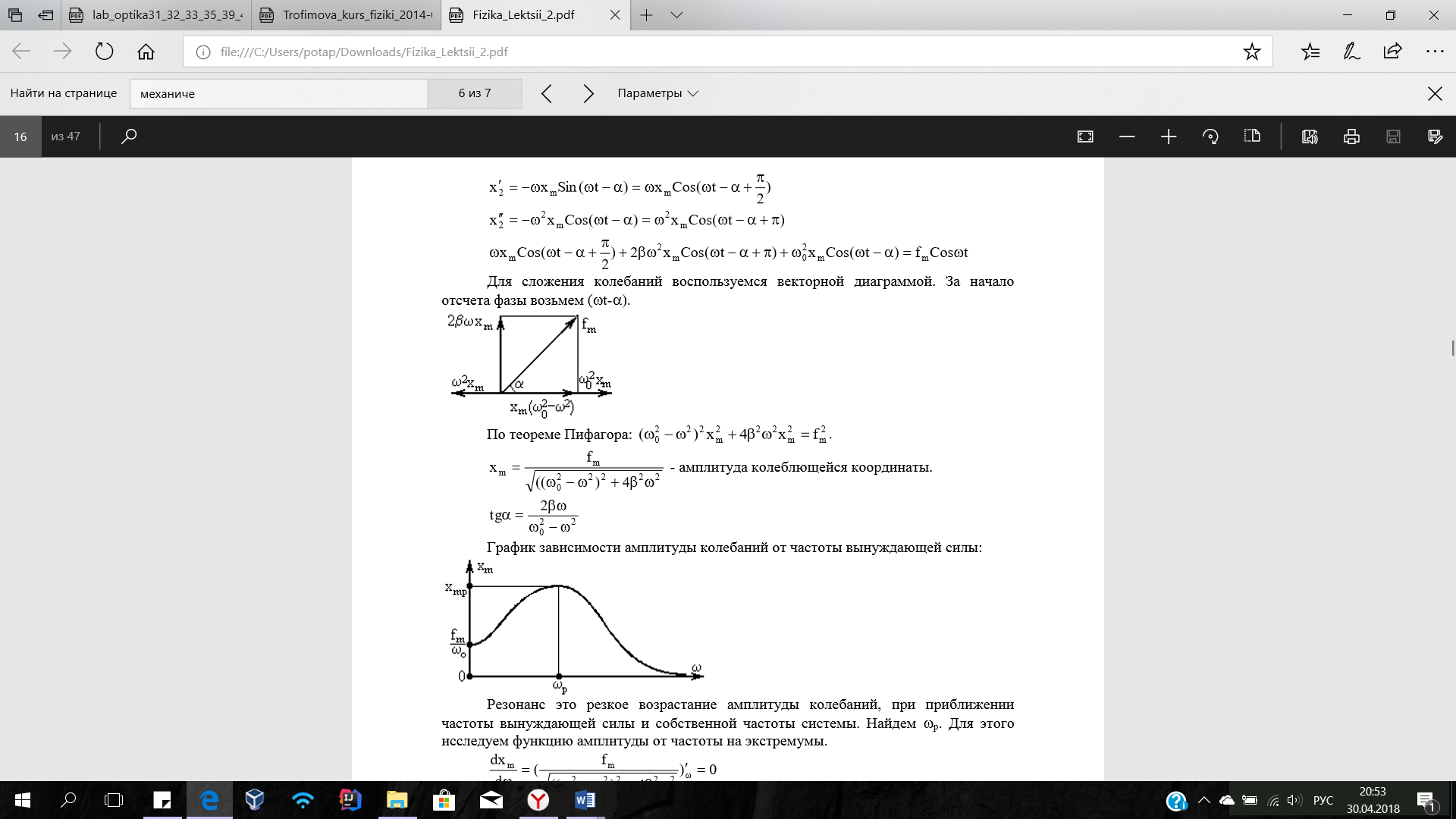
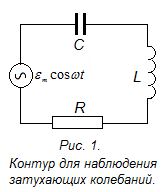1. Вынужденные колебания в RLC-контуре. Вывод дифференциального уравнения вынужденных колебаний.

Вынужденными называются такие колебания, которые происходят в колебательной системе под влиянием внешнего периодического воздействия.

Рассмотрим процессы, протекающие в электрическом колебательном контуре (рис. 1), присоединенном к внешнему источнику, ЭДС которого изменяется по гармоническому закону

,

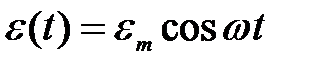где e_m – амплитуда внешней ЭДС,

w – циклическая частота ЭДС.

Обозначим через U_C напряжение на конденсаторе, а через i - силу тока в контуре. В этом контуре кроме переменной ЭДС e (t) действует еще ЭДС самоиндукции e_L в катушке индуктивности.

ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока в контуре

.

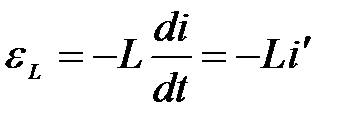Для вывода дифференциального уравнения вынужденных колебаний, возникающих в таком контуре используем второе правило Кирхгофа

.

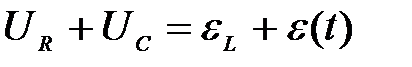Напряжение на активном сопротивлении R найдем по закону Ома

.

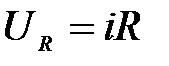Cила электрического тока равна заряду протекающему за единицу времени через поперечное сечение проводника

.

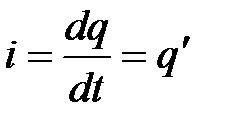Следовательно

.

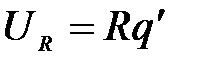Напряжение U_C на конденсаторе прямо пропорционально заряду на обкладках конденсатора

.

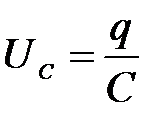ЭДС самоиндукции можно представить через вторую производную от заряда по времени

.

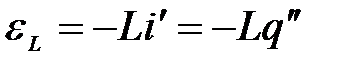Подставляя напряжения и ЭДС во второе правило Кирхгофа

.

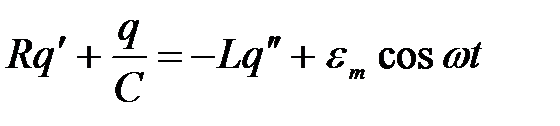Разделив обе части этого выражения на L и распределив слагаемые по степени убывания порядка производной, получим дифференциальное уравнение второго порядка

.

Введем следующие обозначения и получим

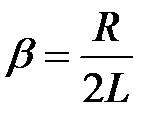– коэффициент затухания,

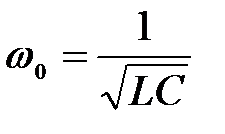– циклическая частота собственных колебаний контура.