Элементарная теория дисперсии

Мы получили связь групповой и фазовой скорости

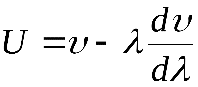(14.1)

Из этого условия следует, что может происходить «расползание» волнового пакета и формула 14.1, полученная для малых изменений волнового числа, становится неточной и понятие групповой скорости теряет смысл. Но и в таких условиях скорость передачи сигнала не превышает скорости света в вакууме. Для иллюстрации этого фундаментального положения приведем следующую схему явления. Пусть среду, в которой распространяется исследуемый волновой пакет (импульс), составляют элементарные осцилляторы (атомы), произвольно распределенные в вакууме. Когда передний край импульса (распространяющийся со скоростью с) дойдет до какого-либо атома среды, он раскачает его осциллирующий электрон и последний начнет излучать. Но этот процесс неизбежно должен характеризоваться какой-то инерционностью. Возникшее излучение, которое также движется со скоростью с (атомы находятся в пустоте), внесет свой вклад структуру волнового пакета, но не может повлиять на скорость распространения его переднего края (фронта волны) — она по-прежнему будет равна скорости света в вакууме и не зависит от того, что происходит с импульсом.

УРАВНЕНИЯ ДИСПЕРСИИ

Сложная задача взаимодействия электромагнитного поля с веществом может решаться как методами классической, так и квантовой физики. Следует учитывать, что при использовании гармонического осциллятора в качестве модели излучающего атома результаты квантовой и классической теории дисперсии полностью совпадают. В последующем изложении, проводимом в приближении классической физики, фактически использована модель Томсона — атом как гармонический осциллятор с частотой собственных колебаний w0. Идея расчета, впервые проведенного Лоренцем, предельно проста: для получения зависимости показателя преломления какого-либо вещества от частоты падающего на него света нужно найти вектор поляризации этого вещества Р, создаваемый полем световой волны Е. Затем вычисляют вектор электростатической индукции

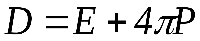(14.2)

и определяют диэлектрическую проницаемость вещества 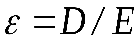, Используя основное соотношение электромагнитной теории света 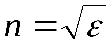зависимость показателя преломления от частоты падающего света получают зависимость 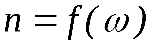. Таким образом, изменениеnв зависимости отwобусловливается суперпозицией первичной световой волны и всех вызванных ею вторичных волн в исследуемом веществе, свойства которого должны существенно влиять на ход показателя преломленияn(w). Важно понять, что в данном случае первичная волна не заменяется суммой вторичных волн (как это делается при истолковании явления дифракции) а взаимодействует с ними. Уточним постановку задачи: пусть в единице объема имеется N хаотически расположенных эквивалентных атомов исследуемого вещества. Будем считать, что в каждом атоме имеется один оптический электрон с зарядом q. Электрическое поле световой волны воздействует на такой электрон с силой qE (вынуждающая сила).

Не будем пока учитывать действия на данный электрон поля, создаваемого всеми другими электронами. Это пренебрежение справедливо при малой плотности изучаемого вещества. В дальнейшем будет показано, как видоизменяются формулы при учете взаимодействия электрических зарядов

Электрон удерживается в атоме квазиупругой силой fr, которая, как мы видим, пропорциональна смещению электрона г, возникающему под действием поля световой волны. Масса электронаmи коэффициент квазиупругой связиfопределяют частоту собственных колебаний гармонического осциллятораw0. Связь между ними записывается в виде /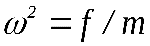

Будем считать, что все гармонические осцилляторы идентичны, т е. имеют одну собственную частоту колебания w0. Заметим, что исходные положения излагаемой теории пригодны не только для описания колебаний оптических электронов, но их можно использовать для учета вынужденных колебаний ионов с частотами В этом случае в кубе с ребром порядка длины световой волны даже при очень малой плотности вещества содержится громадное количество излучающих атомов, которые, как мы условились, не влияют друг на друга, и можно положить, что поляризация вещества в поле световой волны определяется соотношением Р =Nqr.

Таким образом, можно считать выясненным вопрос о необходимости введения в уравнение движения осциллирующего электрона вынуждающей и квазиупругой сил. Теперь уточним их знаки.

Квазиупругая сила всегда имеет знак обратный направлению смещения, т. е. равна –fr. Знак вынуждающей силыqЕ, так же как и поляризация среды, зависит от знака электрического заряда. Выше поляризация среды была определена выражением Р =Nqr. Поэтому введем в уравнение движения вынуждающую силу +qEчто будет годиться для описания движения как положительного, так и отрицательного заряда.

Необходимо разобраться еще в одном вопросе: как учесть неизбежное затухание колебаний осциллятора? Физические причины, приводящие к затуханию излучения и связанному с ним уширению спектральной линии, будут подробно обсуждены ниже. Они сводятся к потере энергии вследствие излучения, к столкновениям, тушащим колебания осцилляторов, и к хаотическому тепловому движению атомов (эффект Доплера). При феноменологическом описании можно объединить все эти разнородные процессы, вводя убывающую во времени амплитуду затухающей волны. При составлении уравнения движения осциллирующего электрона для учета затухания нужно ввести какую-то тормозящую силу. Запишем ее в виде —gr, где g — некий коэффициент; частное от его деления на массу электрона обозначают gи называют коэффициентом затухания.

В теории колебаний доказывается, что тормозящая сила пропорциональна скорости движения в том случае, когда затухание относительно мало и в незначительной степени искажает собственные колебания системы. Простые оценки показывают, что в данной задаче такое приближение законно. Упоминавшиеся выше причины (столкновения, тепловое движение) могут в 10—100 раз уширить линию излучения, но и при этом в полной мере сохраняется основной результат — в течение одного периода атом теряет очень малую часть накопленной энергии, и, следовательно, введение такой тормозящей силы в уравнение движения остается вполне законным.

Итак, дифференциальное уравнение движения осциллирующего электрона имеет вид

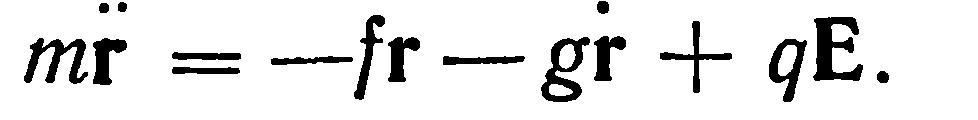(14.3)

Напомним, что g/m=gи 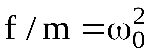.Перегруппировав члены , найдем

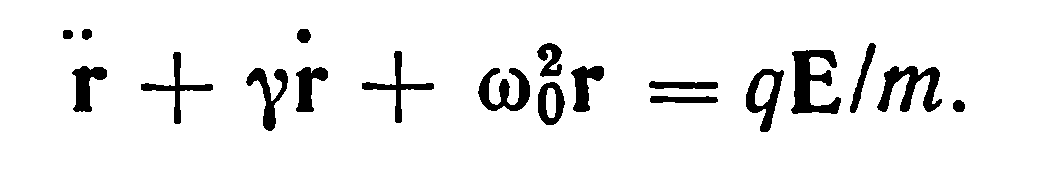(14.4)

Будем исходить из того, что напряженность электрического поля изменяется по закону Е=Еоcos(wt+j) и предполагая, что трение минимально, т.е.g=0, решение этого уравнения следует искать в ви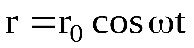де

, где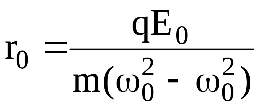

Найдем значение вектора поляризации

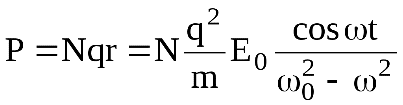
и подставим в 14.2

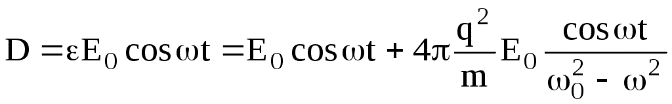(14.5)

сократив в уравнении (14.5) слева и справа 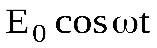и учтя, что 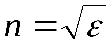, получаем

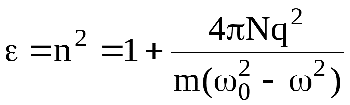(14.6)

Уравнение (14.6) показывает, что дисперсия создается в результате колебаний электронов.

Проанализируем уравнение (14.6).

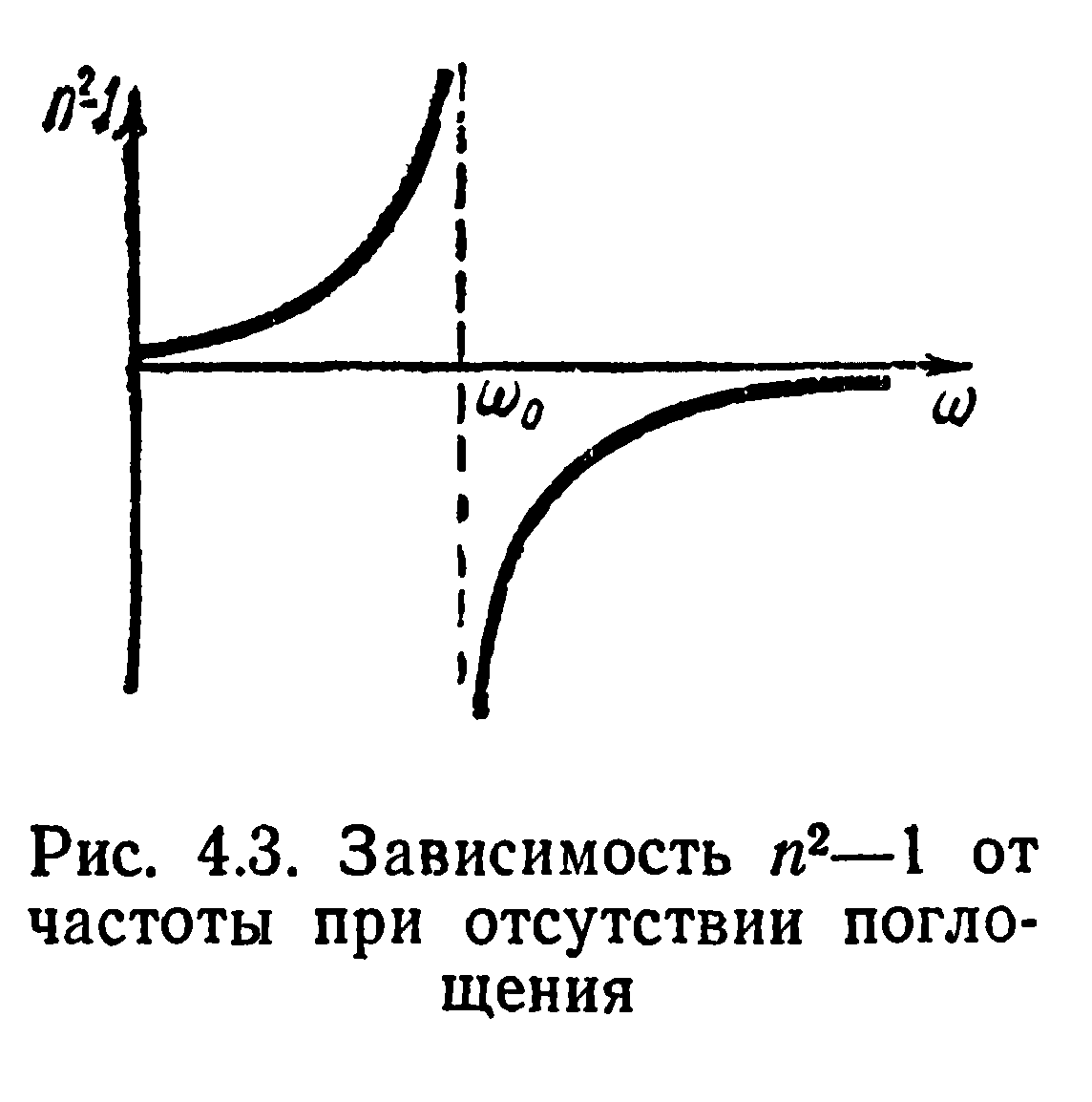
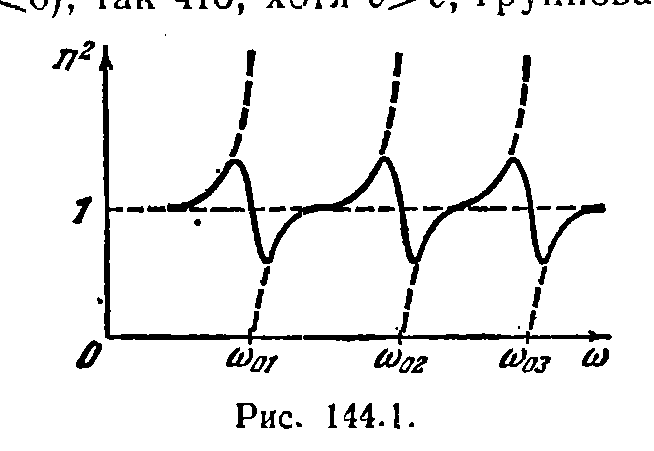
При частотах w, заметно отличающихся от собственной частоты колебаний электроновw0 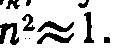. Вблизи собственных частот функция 14.6 терпит разрыв: при стремленииwкw0 c слева она обращается в +¥, при стремлении справа — в —¥(см. пунктирные кривые на рис. 4.3). Такое поведение функции (14.6) обусловлено тем, что мы пренебрегли трением излучения (напомним, что при пренебрежении трением амплитуда вынужденных колебаний при резонансе обращается в бесконечность). Учет трения излучения приводит к зависимостиn2отw, показанной на рис. 144.1 сплошной кривой.

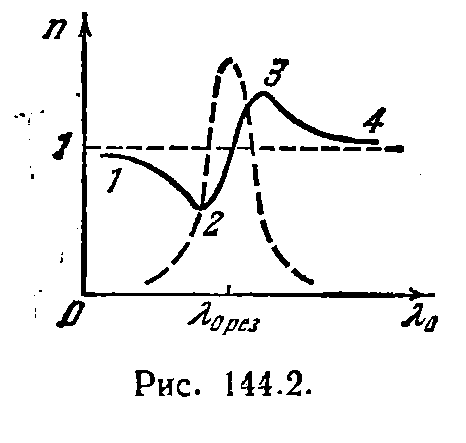
Перейдя от 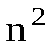кnи отwкlо, получим кривую, изображенную на рис. 144.2 (дан лишь участок кривой в области одной из резонансных длин волн). Пунктирная кривая на этом рисунке изображает ход коэффициента поглощения света веществом. Участок 3—4 аналогичен кривой, приведенной на рис. 142.1. Участки 1—2 и 3—4 соответствуют нормальной дисперсии (dn/dlо<.0). На участке 2—3 дисперсия аномальна (dn/dlо>0).

В области 1—2 показатель преломления меньше единицы, следовательно, фазовая скорость волны превышает с. Это обстоятельство не противоречит теории относительности, основывающейся на утверждении, что скорость передачи сигнала не может превзойти с. В предыдущем параграфе мы выяснили, что передать сигнал с помощью идеально монохроматической волны невозможно. Передача же энергии (т. е. сигнала) с помощью не вполне монохроматической волны (группы волн) осуществляется со скоростью, равной групповой скорости. В области нормальной дисперсии du/dl>0 (dn и duимеют разные знаки, a dn/dl<0), так что, хотяu>c, групповая скорость оказывается меньше с.

В области аномальной дисперсии понятие групповой скорости теряет смысл (поглощение очень велико). Поэтому вычисленное по 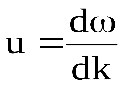значение и не будет характеризовать скорости передачи энергии. Соответствующий расчет дает и в этой области для скорости передачи энергии значение, меньшее с.

Дисперсия возникает в результате интерференции первичной и вторичной волн. Поэтому передний фронт светового импульса распространяется в среде со скоростью света в вакууме, поскольку вторичные волны не могут его догнать. Эта часть.импульса' прибывает первой. Ее амплитуда мала. Затем прибывает вторая часть импульса, имеющая более значительную амплитуду и продолжительность. Затем прибывает основной сигнал. Ясно, что скорость сигнала не является точно определенным понятием, поскольку за сигнал можно было бы принять часть импульса, прибывающей в точку приема первой. Обычно, говоря о скорости сигнала, имеют в виду групповую скорость на частоте, соответствующей максимальной амплитуде в сигнале. Однако при достаточной чувствительности детектора за скорость сигнала можно было бы принять скорость предшественников основного сигнала. В этом случае скорость сигнала может быть сколь угодно близкой к скорости света в вакууме, хотя сигнал и распространяется в среде.

Тепловое излучение. Поток энергии. Энергетическая совместимость. Испускательная способность зависимость от частоты при разных температурах (графики). Поглощательная способность. Абсолютное черное тело. Серое тело.

Тепловое излучение - электромагнитное излучение, испускаемое веществом и возникающее за счет его внутренней энергии.

Тепловое излучение обусловливается возбуждением частиц вещества при соударениях в процессе теплового движения или ускоренным движением зарядов (колебания ионов кристаллической решетки, тепловое движение свободных электронов и т.д.). Оно возникает при любых температурах и присуще всем телам. Характерной чертой теплового излучения является сплошной спектр.

Интенсивность излучения и спектральный состав зависят от температуры тела, поэтому не всегда тепловое излучение воспринимается глазом как свечение. Например, тела, нагретые до высокой температуры, значительную часть энергии испускают в видимом диапазоне, а при комнатной температуре почти вся энергия испускается в инфракрасной части спектра.

 

Нагретое тело генерирует электромагнитное излучение. Это излучение называется тепловое излучение.

Тепловое излучение имеет непрерывный спектр:

Форма спектра зависит от температуры и материала спектра.

Абсолютно черное тело – тело, которое поглощает всё излучение, падающее на него.

Спектр излучения абсолютно черного тела не зависит от материала тела и определяется только его температурой (реально таких тел не существует).

Хорошей моделью абсолютно черного тела является замкнутая полость с небольшим отверстием в стенке.

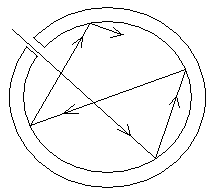
Излучение, падающее в отверстие снаружи, практически полностью поглощается стенками полости.

Если стенки имеют абсолютную температуру не равную нулю, то внутреннее пространство заполнено электромагнитным излучением. Электромагнитные волны излучаются стенками полости. Спектр излучения выходящих из отверстия волн практически полностью совпадает со спектром излучения абсолютно черного тела.

При тепловом равновесии излучение внутри полости можно считать излучением абсолютно черного тела, следовательно, спектр этого излучения определяется только температурой тел и не зависит от их материала.

Мода излучения – это стоячая волна, образующаяся внутри полости.

 

Число мод или стоячих волн с частотой меньше ν:

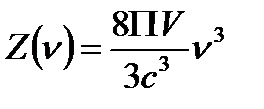
с = 3*108 м/с

V – объём полости

ν - частота

 

Число мод от ν до ν + dν:

 

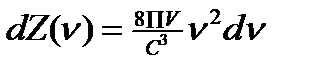
Плотность энергии – энергия единицы объёма занятого излучением с частотой в единичном интервале частот.

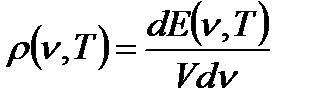
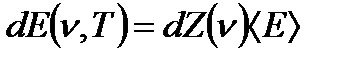
dE – энергия излучения с частотой в интервале dν.

<E> - средняя энергия моды с частотой ν.

 

Гипотеза Планка.

Планк предположил, что энергия моды излучения может принимать только дискретный набор значений, то есть энергия должна быть кратна некоторой минимальной энергии Е0:

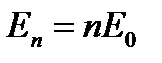, n = 1,2,3…

Эта гипотеза нужна, чтобы получить правильное выражение для плотности энергии.

Закон Больцмана.

Вероятность Wn такова, что модуль излучения имеет энергию En.

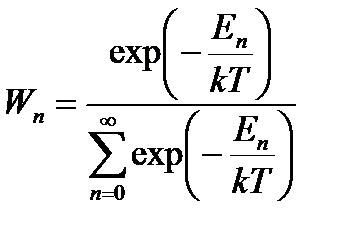
K = 1, 38 * 10 –23 Дж/К – постоянная Больцмана

Т – абсолютная температура

 

Средняя энергия моды излучения:

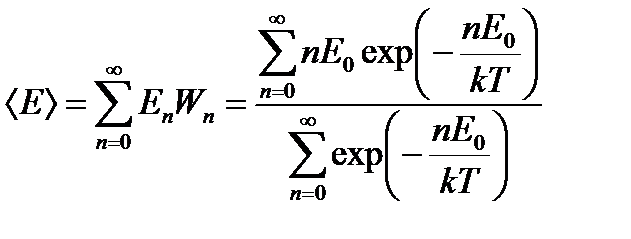
После преобразований получим:

 

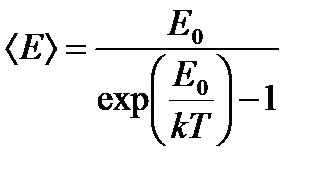
Рассмотрим классический предел:

В классической физике энергия может принимать любые значения, это значит, что Е0 стремится к нулю.

Средняя энергия моды в классическом пределе:

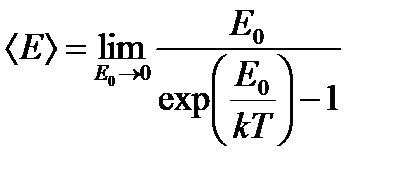
Ультрафиолетовая катастрофа.

В классическом пределе плотность энергии при больших частотах стремится к бесконечности.

Найдём выражение для плотности энергии в классическом пределе.

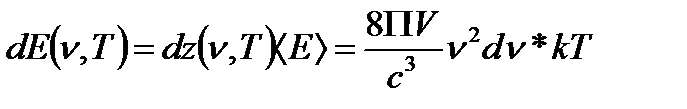
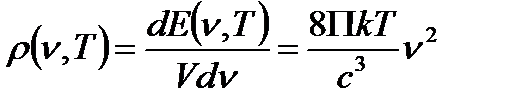
Это выражение противоречит опыту.

 

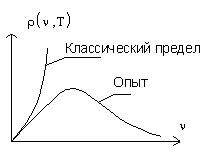
Ультрафиолетовая катастрофа послужила первой причиной создания квантовой механики.

 

Квантовая гипотеза.

Энергия излучения может меняться только порциями или квантами. Квант энергии пропорционален частоте излучения.

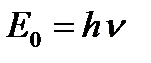
h = 6, 63 * 10-34 Дж*с – постоянная Планка.

 

Средняя энергия моды с учетом квантовой гипотезы.

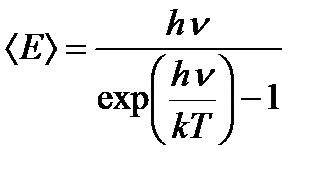
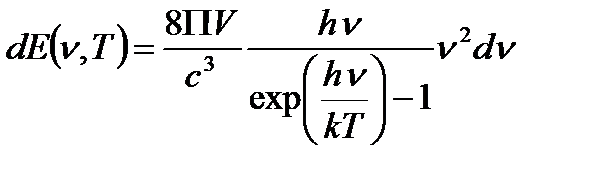
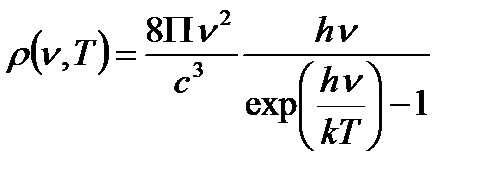
Спектральная плотность энергетической светимости (испускательная способность) – энергия, излучаемая телом за единицу времени с единицы площади поверхности в единичном интервале частот.

 

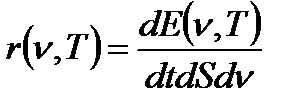
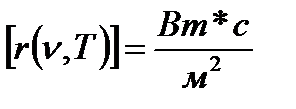
Поток энергии – энергия, излучаемая в единицу времени.

Спектральная плотность энергетической светимости однозначно связана с плотностью энергии.

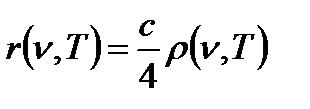
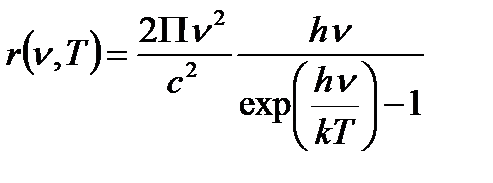- формула Планка.

 

Построим график r = r(λ,T) для различных температур.

 

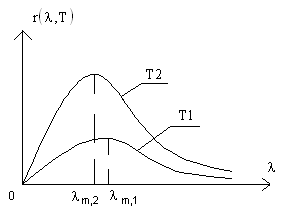
Т2 > Т1

Первый закон Вина (Закон смещения Вина).

При повышении температуры максимум спектральной плотности энергетической светимости смещается в сторону коротких длин волн.

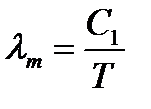С1 = 2,9 * 10-3 м*К – первая постоянная Вина.

λm - длина волны на которую приходится максимум испускательной способности.

 

Второй закон Вина.

Максимум спектральной плотности энергетической светимости пропорционален пятой степени абсолютной температуры.

С2 = 1,29 * 10-5 Вт/м3 * К5 – вторая постоянная Вина.

Энергетическая светимость – энергия, излучаемая телом за единицу времени с единицы площади поверхности во всём интервале частот.

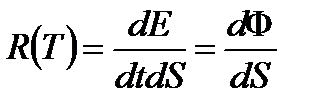
[R] = Вт/м2

 

Закон Стефана – Больцмана.

Энергетическая светимость абсолютно черного тела пропорциональна четвёртой степени абсолютной температуры.

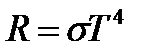σ = 5, 67 * 10-8 Вт/м2К4

Поглощательная способность – отношение потока поглощенного к потоку падающему.

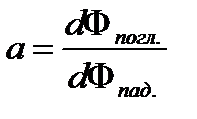
а = 1 (для абсолютно чёрного тела).

 

Закон Кирхгофа.

Отношение спектральной плотности энергетической светимости к поглощателтной способности не зависит от материала тела и является универсальной функцией частоты, температуры.

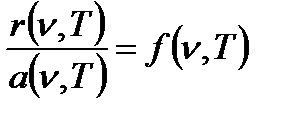
Универсальная функция – испускательная способность абсолютно черного тела.

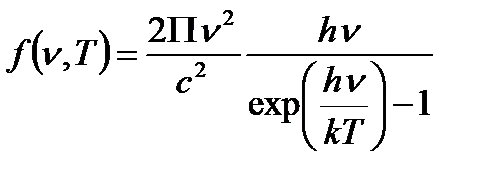
Энергетическая светимость для серого тела: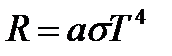

По способности поглощать электромагнитное излучение выделяют два идеальных тела:

абсолютно черное тело (а.ч.т.) – тело, которое во всем интервале длин волн поглощает полностью падающее на него излучение (a _λ,T = 1);

абсолютно серое тело (а.с.т.) – тело, для которого поглощательная способность во всем интервале длин волн является постоянной величиной, меньшей единицы

(a _{λ, T}= const < 1).

Моделью а.ч.т. можно считать полость внутри тела, которое имеет малое входное отверстие (рис. 6.4). Действительно, все излучение, попадающее в эту полость, практически не выходит наружу. Это связано с тем, что при многократных отражениях от стенок полости энергия падающего излучения практически полностью поглощается. Следовательно, поглощательная способность такой полости во всем интервале длин волн будет равна единице, и тогда выходящее из полости тепловое излучение представляет собой излучение а.ч.т.

 

Законы теплового излучения. Невозможность их объяснения классической физикой. Квантовая постоянная Планка. Формула.

Тепловое излучение - электромагнитное излучение, испускаемое веществом и возникающее за счет его внутренней энергии.

Тепловое излучение обусловливается возбуждением частиц вещества при соударениях в процессе теплового движения или ускоренным движением зарядов (колебания ионов кристаллической решетки, тепловое движение свободных электронов и т.д.). Оно возникает при любых температурах и присуще всем телам. Характерной чертой теплового излучения является сплошной спектр.

Интенсивность излучения и спектральный состав зависят от температуры тела, поэтому не всегда тепловое излучение воспринимается глазом как свечение. Например, тела, нагретые до высокой температуры, значительную часть энергии испускают в видимом диапазоне, а при комнатной температуре почти вся энергия испускается в инфракрасной части спектра.

Закон Кирхгофа - отношение испускательной способности тела к его поглощательной способности одинаково для всех тел и равно спектральной плотности энергетической светимости абсолютно черного тела:

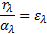
Закон Стефана-Больцмана - энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры:

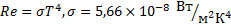
Для серого тела верхняя формула принимает вид:

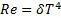
где 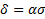– приведенный коэффициент поглощения.

Закон смещения Вина – длина волны, на которую приходится максимум испускательной способности абсолютно черного тела (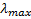), обратно пропорциональна его абсолютной температуре:

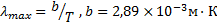
При повышении температуры максимум испускательной способности смещается влево

В 1900 г. М. Планк получил формулу для расчета испускательной способности абсолютно черного тела теоретически. Для этого ему пришлось отказаться от классических представлений о непрерывности процесса излучения электромагнитных волн. По представлениям Планка, поток излучения состоит из отдельных порций - квантов, энергии которых пропорциональны частотам света:

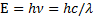
где v – частота; 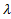– длина волны; с – скорость света в вакууме; h – коэффициент пропорциональности, называемый постоянной Планка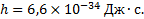

Каждый отдельный квант несет ничтожно малую энергию. Поэтому при больших потоках излучения его дискретная природа незаметна.

Приведем формулу Планка для испускательной способности абсолютно черного тела:

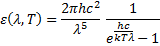
Где с – скорость света в вакууме; k – постоянная Больцмана.