Пусть какой-то ресурс имеется у центра, и он необходим агентам. Задача центра – распределить его между агентами. Если центр знает эффективность использования ресурса подчиненными, то задача заключается в том, как распределить ресурс, например, чтобы суммарный эффект от его использования был максимальным. Если агенты являются активными, а центр не знает эффективности использования ресурса, и спрашивает у них: кому сколько ресурса нужно, и кто как будет его использовать, то, если ресурс ограничен, то агенты в общем случае не сообщат честно, кому сколько нужно, и ресурсов на всех не хватит. В каких ситуациях управляющий орган может предложить такую процедуру, то есть правило распределения ресурсов между агентами, которая была бы неманипулируема, то есть такую процедуру, чтобы каждому из агентов было выгодно говорить правду, независимо от того, сколько ресурса ему надо?
Рассмотрим механизм распределения ресурсов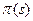 
, который обладает следующими свойствами:
1) процедура планирования непрерывна и монотонна по сообщениям агентов (монотонность означает, что чем больше просит агент ресурса, тем больше он его получает);
2) если агент получил некоторое количество ресурса, то он может, изменяя свою заявку, получить и любое меньшее количество ресурса;
3) если количество ресурса, распределяемое между группой агентов, увеличилось, то каждый из агентов этой группы получит не меньшее количество ресурсов, чем раньше.
Целевая функция агента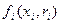 
зависит от типа ri данного агента, который в случае механизмов распределения ресурса будет рассматриваться как оптимальное количество ресурса для данного агента.
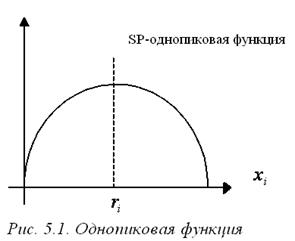
Допустим, что целевая функция агента имеет единственный максимум по xi в точке пика. То есть агенту нужно некоторое количество ресурса, если ему недодают ресурса – его полезность при этом меньше, если ему дают лишний ресурс – его полезность тоже меньше. Единственным максимумом может быть и бесконечность, то есть целевая функция может монотонно возрастать. Такие функции предпочтения называются однопиковые (см. рис. 5.1).
Рассмотрим сначала пример, а потом приведем общие результаты.
Пример 5.1. Пусть n= 3,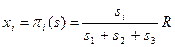 
, R – количество ресурса, 
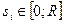. Пусть R =1; r 1 = 0,3; r 2=0,4; r 3=0,5. Имеем: r 1+ r 2+ r 3=1,2> R =1.
1) Пусть каждый агент сообщает правду, тогда:
;
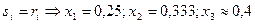2) Пусть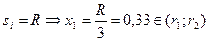 
. Первый агент решает задачу: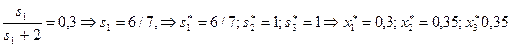 
Это - равновесие Нэша. 
Приоритетные механизмы. В приоритетных механизмах распределения ресурса, как следует из их названия, при формировании планов (решении о том, сколько ресурса выделить тому или иному агенту) в существенной степени используются показатели приоритета агентов. Приоритетные механизмы в общем случае описываются следующей процедурой:
,
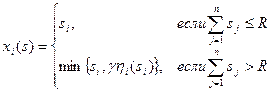где n - число агентов,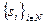 
- их заявки, 
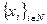- выделяемые количества ресурса, R - распределяемое количество ресурса, 
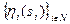- функции приоритета агентов, 
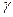- некоторый параметр.
Операция взятия минимума содержательно означает, что агент получает ресурс в количестве, не большем запрошенной величины. Параметр 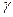играет роль нормировки и выбирается из условия выполнения балансового (бюджетного) ограничения:
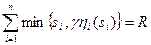
то есть подбирается таким, чтобы при данных заявках и функциях приоритета в условиях дефицита распределялся в точности весь ресурс R.
Приоритетные механизмы, в зависимости от вида функции приоритета, подразделяются на три класса - механизмы прямых приоритетов (в которых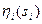 
- возрастающая функция заявки 
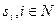), механизмы абсолютных приоритетов, в которых приоритеты агентов фиксированы и не зависят от сообщаемых ими заявок (Так как в механизмах абсолютных приоритетов планы, назначаемые агентам, не зависят от их заявок, то в рамках гипотезы благожелательности можно считать любой механизм абсолютных приоритетов неманипулируемым. Недостатком этого класса механизмов можно считать то, что в них центр никак не использует информации, сообщаемой агентами.) и механизмы обратных приоритетов (в которых 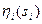– убывающая функция заявки 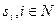). Рассмотрим последовательно механизмы прямых и обратных приоритетов.
Механизмы прямых приоритетов. Процедура распределения ресурса пропорционально заявкам, называется механизмом пропорционального распределения:
.
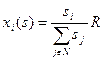Это – самый распространенный способ распределения ресурса. Видно, что данная процедура распределения ресурса удовлетворят условию нормировки. При любых комбинациях сообщений агентов распределяется в точности весь ресурс. Условия непрерывности и монотонности также выполнены.
Предположим, что сообщение каждого агента лежит в диапазоне от нуля до всего количества ресурсов, то есть, как минимум, агент может отказаться от ресурса, как максимум, может попросить весь ресурс, который имеется у центра.
Если агент получил некоторое количество ресурса, то, уменьшая заявку, в силу непрерывности и монотонности процедуры распределения ресурса, он всегда может получить меньшее количество, вплоть до нуля.
Если каждый агент скажет правду, сколько ему нужно, тогда он получит меньше, что логично, потому что ресурсов не хватает, агенты сказали правду и были «пропорционально урезаны».
Предположим, что игру центр разыгрывает неоднократно. На втором шаге агенты попросят больше. Если каждый будет просить максимально возможную заявку, то все получат поровну. Если кому-то этого много, то излишки он может отдать другому, но кому-то все равно не хватит.
Данный механизм является манипулируемым, потому что агентам невыгодно сообщать достоверную информацию о своих типах – тех количествах ресурса, которое им необходимо.
Итак, выше рассмотрен пример механизма распределения ресурса. Рассчитано равновесие. Запишем результаты исследования таких механизмов в общем виде. Для этого попробуем сначала понять, какими свойствами характеризуется равновесие. Агентов можно разделить на две категории:
1) «приоритетные » агенты (диктаторы) – те, кто получают абсолютно оптимальные для себя значения плана, то есть планы, равные их типам (при механизме распределения ресурса – те агенты, которые получают ресурса ровно столько, сколько им нужно),
2) «обделенные » агенты – те, кому не хватает ресурса, те, кто хоть и просит по максимуму, но в равновесии получает меньше, чем ему нужно.
Следующие два свойства характеризуют равновесие.
Утверждение 5.1.
1) Если некоторый агент в равновесии получает строго меньше ресурса, чем ему необходимо: xi *< ri, то в равновесии он запросит максимально возможное количество ресурса: si *= R.
2) Если кто-то из агентов в равновесии просит строго меньше максимума: si *< R, то это значит, что он получает количество ресурса, оптимальное для него: xi *= ri, то есть является диктатором.
Введем определение анонимного механизма принятия решений, то есть механизма, симметричного относительно перестановок агентов. Анонимность – демократическое требование, например, в процедурах выборов она отражается в том, что на избирательном участке обмен между двумя избирателями пустыми бланками бюллетеней не меняет результата выборов. То есть все находятся в равных условиях. Тогда при перестановке местами агентов соответственно переставляются и планы этих агентов.
Утверждение 5.2.
1) Все анонимные механизмы распределения ресурса эквивалентны между собой, то есть приводят при одних и тех же предпочтениях агентов к одним и тем же равновесным количествам ресурса, которые они получают.
2) Так как механизм пропорционального распределения является анонимным (все агенты входят в него симметрично), а все анонимные механизмы эквивалентны между собой, то это значит, что все механизмы распределения ресурсов, которые являются анонимными, эквивалентны механизму пропорционального распределения.
Итак, любая анонимная процедура, удовлетворяющая перечисленным выше трем требованиям, приводит к одним и тем же результатам. А механизм пропорционального распределения (который является анонимным) достаточно прост по своему виду, поэтому прост и для исследования, и для агентов (ресурс делится пропорционально запросам).
Таким образом, утверждение 5.2 говорит, что не нужно выдумывать сложных механизмов распределения ресурса - если ограничиться классом анонимных механизмов, то достаточно рассмотреть механизм пропорционального распределения. Кроме того, оказывается, что механизм пропорционального распределения эквивалентен механизму последовательного распределения, рассчитать равновесие для которого совсем просто.
Механизмы последовательного распределения ресурса заключается в следующем. Это - прямой механизм, т.е. каждого агента спрашивают о том, сколько ресурса ему нужно.
Предположим, что агенты сделали свои сообщения. Упорядочим их по возрастанию сообщений (первый попросил меньше всех ресурса, потом второй и т.д.):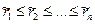 
. Дальше применяем следующий алгоритм последовательного распределения (положив 
):
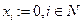Шаг 1. Если мы можем дать каждому агенту столько ресурса, сколько попросил первый агент, то даем всем по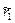 
(если 
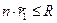, то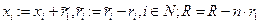 
). Если не можем, распределяем ресурс между всеми агентами поровну (если 
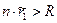, то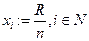 
)и останавливаем алгоритм.
Шаг 2. Исключаем первого агента из рассмотрения, перенумеровываем агентов и возвращаемся к шагу 1.
Пример 5.2.1. Пусть R=1, r 1 = 0,3; r 2=0,4; r 3=0,5; 0,3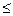 
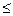0,4 0,5.
Предположим, что все агенты сообщили правду, тогда мы можем дать всем одновременно по минимуму - 0,3: x 1=0,3; x 2=0,3; x 3=0,3.
После первого шага: r 1 = 0; r2= 0,1; r 3=0,2; R= 0,1. Первый агент удовлетворен полностью. Поэтому забываем про него и повторяем для тех, кому ресурс еще необходим. Остаток ресурса, равный 0,1, недостаточен для того, чтобы дать обоим агентам столько, сколько требует первый (бывший второй) – по 0,1, следовательно, мы должны остаток ресурса поделить поровну, т.е. по 0,05. В результате второй агент получит 0,35, третий тоже 0,35:
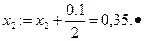
Так работает механизм последовательного распределения. Понятно, что максимум через n шагов, где n – количество агентов, процедура остановится.
Легко показать (сделайте это самостоятельно), что в механизме последовательного распределения ресурса агентам выгодно сообщать достоверную информацию, т.е. сообщение достоверной информации является доминантной стратегией каждого агента.
Другими словами, механизм последовательного распределения является неманипулируемым прямым механизмом.
Рассмотрим на примере 5.2, может ли кто-то из агентов, сообщая неправду, улучшить свое положение?
Первый агент получает оптимальное количество ресурса, ему нет нужды искажать информацию. Предположим, что начинает изменять свое сообщение второй агент (завышает заявку или занижает). Если он будет уменьшать свою заявку, все изменится в тот момент, когда разность от сообщения окажется такой, чтобы, выдавая столько, сколько просит второй агент, нам хватало бы ресурса. Такая разность равна 0,05 (деление поровну). Это значит, что второй агент должен заявить 0,35. Если он заявляет 0,35, то он получает 0,35, что и получал до этого, т.е. никакой выгоды занижение ему не принесло. Если же он сообщит меньше, чем 0,35, то он и получит столько, сколько сообщит, т.е. меньше 0,35. Ему это не выгодно, т.к. в действительности ему требуется 0,4. Таким образом, уменьшать заявку ему не выгодно.
Если же он начинает просить больше, чем 0,4, то вообще ничего не изменится, т.к. на втором шаге ресурса и так не хватает, и его остаток делится поровну между вторым и третьим агентами.
Аналогично для других агентов показывается, что, увеличивая или уменьшая до определенного уровня заявку, они ничего для себя не меняют, а дальнейшее уменьшение заявки дает уменьшение количества получаемого ими ресурса.
Механизмы обратных приоритетов. Механизмы обратных приоритетов, в которых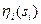 
является убывающей функцией 
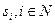, обладают рядом преимуществ по сравнению с механизмами прямых приоритетов. Проведем анализ механизма обратных приоритетов с функциями приоритета
,
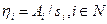где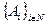 
- некоторые константы (отметим, что механизм обратных приоритетов не удовлетворяет условию монотонности). Величина Aі характеризует потери ОС, если i -й агент вообще не получит ресурса. Тогда отношение Ai/si определяет удельный эффект от использования ресурса. Поэтому механизмы обратных приоритетов иногда называют механизмами распределения ресурса пропорционально эффективности (ПЭ-механизмами).
Пример 5.2.2. Пусть имеются три агента (n= 3), А1=16, А2= 9, А3= 4; R= 18. Предположим сначала, что целью агентов является получение максимального количества ресурса. Определим ситуацию равновесия Нэша. Легко заметить, что функция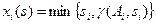 
достигает максимума по si в точке, удовлетворяющей условию 
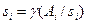. Следовательно, 
.
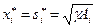Определим параметр 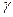из балансового ограничения 
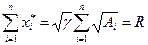. Тогда 
.
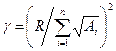Для рассматриваемого примера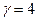 
, а равновесные заявки, определяемые из условия 
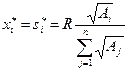, равны: s 1 *= 8; s 2 *= 6, s 3 *= 4.
Проверим, что это действительно равновесие Нэша. Возьмем первого агента. Если он уменьшит свою заявку: s 1 = 7< s1*, то s 1 + s 2* + s 3*< R. Следовательно, x 1 =s1= 7< x 1 *. Если же s1=9>s1*, то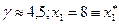 
.
Легко показать, что вычисленные стратегии являются для агентов гарантирующими, то есть максимизируют их выигрыши при наихудших стратегиях остальных.
Если функции предпочтения агентов имеют максимумы в точках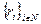 
и если si* > ri, то i -й агент закажет ровно ri и столько же получит, так как при уменьшении заявки его приоритет возрастает.
Именно таким образом выделяется множество приоритетных потребителей ресурса. •
Более того, можно показать, что при достаточно большом числе агентов механизм обратных приоритетов со штрафами за несовпадение ожидаемого и планируемого эффектов оптимален в смысле суммарной эффективности.