Модель информационного управления

С теоретико-игровой точки зрения задача управления состоит в том, чтобы сформировать для управляемых субъектов (агентов) такую игру, чтобы ее исход был наиболее благоприятным для управляющего органа (центра). Соответственно, задачу информационного управления можно неформально (качественно) сформулировать следующим образом: найти такую структуру информированности, чтобы исход рефлексивной игры (см. раздел 6.2) агентов (информационное равновесие) был бы наиболее благоприятен для центра.

Перейдем к формальной постановке задачи. Пусть на множестве действий реальных агентов и структур информированности задана целевая функция центра Ф(x, I). Пусть, далее, центр может сформировать любую структуру информированности из некоторого множества 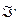. При структуре информированности 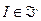вектор действий реальных агентов является элементом множества равновесных векторов 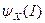. Множество 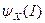может быть пустым, тогда центр, ввиду отсутствия равновесия, не может рассчитывать на тот или иной исход игры. Поэтому введем множество допустимых структур, для которых существует хотя бы одно равновесие: .

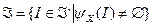Если при заданной структуре 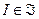множество равновесных векторов 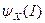состоит более чем из одного элемента, то обычно принимается одно из следующих двух предположений:

1) гипотеза благожелательности (ГБ), состоящая в том, что у центра есть возможность обеспечить выбор агентами «нужного» равновесия;

2) принцип максимального гарантированного результата (МГР), состоящий в том, что центр рассчитывает на наихудшее для себя равновесие игры агентов.

В соответствии с ГБ и МГР получаем, соответственно, постановку задачи информационного управления в двух вариантах:

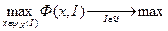; (6.1)

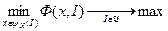. (6.2)

Разумеется, в случае, когда для любого 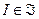множество 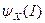состоит ровно из одного элемента, (6.1) и (6.2) совпадают.

Задачу (6.1) (либо (6.2)) будем называть задачей информационного управления в форме целевой функции.

Опишем теперь задачу информационного управления в несколько иной постановке, не зависящей от целевой функции центра. Пусть центр стремится добиться от агентов выбора вектора действий 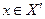. Зададимся вопросом: для каких векторов х и каким образом (то есть при помощи формирования какой структуры I) центр может это сделать? Иначе говоря, вторая возможная постановка задачи информационного управления состоит в нахождении множества достижимости - множества векторов 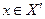, для каждого из которых множество структур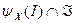

(6.3) непусто,

либо

(6.4) состоит ровно из одного элемента,

а также соответствующих допустимых структур информированности 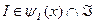для каждого такого вектора х. Условие (6.3) соответствует ГБ, условие (6.4) - МГР.

Задачу (6.3) (либо (6.4)) будем называть задачей информационного управления в форме множества достижимости.

Еще раз подчеркнем, что вторая постановка не зависит от целевой функции центра и отражает лишь его возможность при помощи информационного управления привести систему в то или иное состояние.

Как в первой, так и во второй постановке центр может либо интересоваться, либо не интересоваться стабильностью (см. раздел 6.3) получившегося информационного равновесия. Если требуется осуществить стабильное информационное управление, то есть привести систему в стабильное информационное равновесие, то в приведенных выше постановках требуется заменить 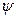на 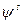, а термины «равновесие» и «равновесный» – на «стабильное равновесие» и «стабильно-равновесный» соответственно.

Моделирование информационного управления. Предлагаемая модель информационного управления представлена на рис. 6.1.

Модель включает в себя агента (агентов) и управляющий орган – центр. Каждый агент характеризуется циклом «информированность агента 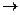действие агента 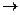наблюдаемый агентом результат 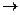информированность агента», и у разных агентов эти три компоненты цикла являются, вообще говоря, различными. В то же время, и это отражает надпись «Агент (ы)» на рис.6.1, можно считать этот цикл общим для всей управляемой подсистемы, то есть для всего набора агентов.

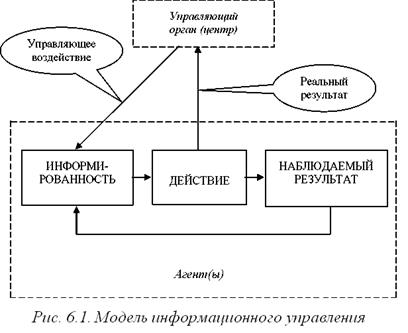
Что касается взаимодействия агента (агентов) и центра, то оно характеризуется:

1) информационным воздействием центра, формирующим ту или иную информированность агента (агентов);

2) реальным результатом действия агента (агентов), который оказывает влияние на интересы центра.

Обсудим модель, изображенную на рис. 6.1, более подробно.

Математическим аппаратом, моделирующим теоретико-игровое взаимодействие агентов, являются рефлексивные игры, в которых агенты выбирают действия на основе своих структур информированности – иерархии представлений о существенных параметрах ситуации («состоянии природы»), представлений о представлениях оппонентов (других агентов) и т.д. Таким образом, в терминах рефлексивных игр информированность агента моделируется при помощи его структуры информированности (соответственно, информированность всей управляемой подсистемы моделируется при помощи структуры информированности игры, являющейся объединением структур информированности агентов).

Исходя из своей структуры информированности, агент выбирает то или иное действие. Для заданной структуры информированности действия агентов являются компонентами информационного равновесия, являющегося решением рефлексивной игры. Информационное равновесие является обобщением равновесия Нэша – наиболее распространенной концепции решения некооперативных игр. Информированность агента о ситуации и о представлениях оппонентов может быть, вообще говоря, неадекватной. Поэтому наблюдаемый агентом результат рефлексивной игры может как соответствовать его ожиданиям, так и не соответствовать им. Соответствие определяется двумя факторами:

1) насколько адекватно информирован агент на момент выбора своего действия;

2) насколько подробную информацию о результатах игры он наблюдает.

Например, наблюдаемым результатом может быть значение его целевой функции, действия оппонентов, истинное значение неопределенного параметра и пр. В общем случае агент наблюдает значение некоторой функции, зависящей от состояния природы и действий оппонентов. Эта функция называется функцией наблюдения, и воздействие ее значения на информированность отображено на рисунке фрагментом «наблюдаемое действие 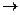информированность». Если все агенты наблюдают именно тот результат, на какой рассчитывают (то есть реальное значение функции наблюдения каждого агента равно ожидаемому), то естественным является предположение о том, что структура информированности не меняется. В этом случае информационное равновесие является стабильным (см. ниже).

Рассмотрим теперь взаимодействие агентов с центром. Осуществляя информационное управление, центр стремится к максимизации своей полезности (разумеется, это относится и к другим типам управления). Если считать, что центр может сформировать любую структуру информированности из некоторого допустимого множества, то задачу информационного управления можно сформулировать следующим образом: найти такую структуру информированности из допустимого множества структур, чтобы полезность центра в информационном равновесии была максимальной (быть может, с учетом затрат центра на формирование структуры).

Подчеркнем следующее важное обстоятельство: в рамках предлагаемой модели мы исходим из предположения о том, что центр может сформировать у агентов любую структуру информированности. За рамками наших рассмотрений остается вопрос о том, каким образом центру следует «убедить» агентов в том, что имеют место те или иные состояния природы и представления оппонентов.

Можно, однако, в рамках рассматриваемой модели классифицировать способы управляющего воздействия на информированность агентов для формирования той или иной структуры. Такими способами являются:

1) информационное регулирование – целенаправленное влияние на информацию о состоянии природы;

2) рефлексивное управление – целенаправленное влияние на информацию о представлениях оппонентов;

3) активный прогноз – целенаправленное сообщение информации о будущих значениях параметров, зависящих от состояния природы и действий агентов.

Классификация задач информационного управления. В лекции рассматриваются двухуровневые ОС с одним центром и многими агентами в условиях неполной информированности агентов – каждый из субъектов может иметь свои представления о природе.

Задачу информационного управления будем рассматривать:

1) в форме целевой функции либо множества достижимости;

2) с использованием гипотезы благожелательности (ГБ) либо принципа максимально гарантированного результата (МГР);

3) с требованием стабильности или без требования стабильности.

Выбор одного из этих восьми вариантов определяется конкретной моделируемой ситуацией. Однако в любом случае необходимым (и, как показывает опыт, наиболее сложным и трудоемким для исследователя) этапом является установление связи между структурой информированности и вектором действий агентов, то есть исследование информационного равновесия.

Рефлексивные игры

Рассмотрим множество N= {1, 2, …, n } агентов. Если в ситуации присутствует неопределенный параметр 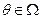(будем считать, что множество 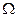является общим знанием), то структура информированности I_i (как синоним будем употреблять термины информационная структура и иерархия представлений) i -го агента включает в себя следующие элементы. Во-первых, представление i -го агента о параметре 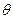– обозначим его 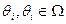. Во-вторых, представления i -го агента о представлениях других агентов о параметре 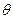– обозначим их 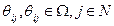. В-третьих, представления i -го агента о представлении j -го агента о представлении k- го агента – обозначим их 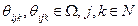. И так далее.

Таким образом, структура информированности I_i i -го агента задается набором всевозможных значений вида 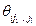, где l пробегает множество целых неотрицательных чисел, 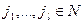, а .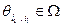

Аналогично задается структура информированности I игры в целом – набором значений 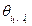, где l пробегает множество целых неотрицательных чисел, 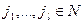, а 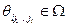. Подчеркнем, что структура информированности I «недоступна» наблюдению агентов, каждому из которых известна лишь некоторая ее часть (а именно – I_i).

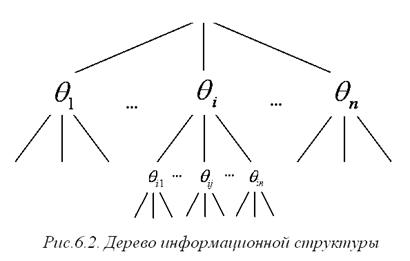
Таким образом, структура информированности - бесконечное n- дерево (то есть тип структуры постоянен и является n -деревом), вершинам которого соответствует конкретная информированность реальных и фантомных агентов.

Рефлексивной игрой Г_I называется игра, описываемая следующим кортежем:

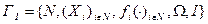, (6.5)

где N - множество реальных агентов, X_i - множество допустимых действий i -го агента, 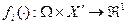- его целевая функция, 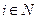, 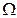- множество возможных значений неопределенного параметра, I - структура информированности.

Таким образом, рефлексивная игра является обобщением понятия игры в нормальной форме, задаваемой кортежем 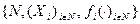, на случай, когда информированность агентов отражена иерархией их представлений (информационной структурой I). В рамках принятого определения «классическая» игра в нормальной форме является частным случаем рефлексивной игры - игры с общим знанием. В «предельном» случае - когда состояние природы является общим знанием - предлагаемая в настоящей работе концепция решения рефлексивной игры (информационное равновесие - см. ниже) переходит в равновесие Нэша.

Совокупность связей между элементами информированности агентов можно изобразить в виде дерева (см. рис. 6.2). При этом структура информированности i -го агента изображается поддеревом, исходящим из вершины .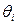

Сделаем важное замечание: в данной лекции мы ограничимся рассмотрением «точечной» структуры информированности, компоненты которой состоят лишь из элементов множества 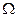. (Более общим случаем является, например, интервальная или вероятностная информированность.)

Стратегическая и информационная рефлексия. Итак, рефлексивной является игра, в которой информированность игроков не является общим знанием. С точки зрения теории игр и рефлексивных моделей принятия решений целесообразно разделять стратегическую и информационную рефлексию.

Информационная рефлексия – процесс и результат размышлений игрока о том, каковы значения неопределенных параметров, что об этих значениях знают и думают его оппоненты (другие игроки). При этом собственно «игровая» компонента отсутствует, так как никаких решений игрок не принимает.

Иными словами, информационная рефлексия относится к информированности агента о природной реальности (какова игра), и о рефлексивной реальности (какой видят игру другие). Информационная рефлексия логически предшествует рефлексии несколько иного рода – стратегической рефлексии.

Стратегическая рефлексия – процесс и результат размышлений игрока о том, какие принципы принятия решений используют его оппоненты (другие игроки) в рамках той информированности, которую он им приписывает в результате информационной рефлексии. Таким образом, информационная рефлексия имеет место только в условиях неполной информированности, и ее результат используется при принятии решений (в том числе – при стратегической рефлексии). Стратегическая рефлексия имеет место даже в случае полной информированности, предваряя принятие игроком решения о выборе действия (стратегии). Другими словами, информационная и стратегическая рефлексии могут изучаться независимо, однако в условиях неполной информированности обе они имеют место.

Далее для формулировки некоторых определений и свойств нам понадобятся следующие обозначения:

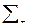– множество всевозможных конечных последовательностей индексов из N;

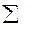– объединение 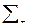с пустой последовательностью;

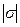– количество индексов в последовательности 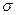(для пустой последовательности принимается равным нулю), которое выше было названо длиной последовательности индексов.

Если 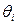- представления i -го агента о неопределенном параметре, а 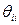- представления i -го агента о собственном представлении, то естественно считать, что 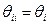. Иными словами, i -й агент правильно информирован о собственных представлениях, а также считает, что таковы и другие агенты и т.д. Формально это означает, что выполнена аксиома автоинформированности, которую далее будем предполагать выполненной:

.

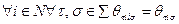Эта аксиома означает, в частности, что, зная 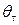для всех 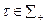таких, что 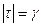, можно однозначно найти 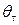для всех 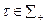таких, что .

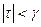Наряду со структурами информированности I_i, 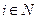, можно рассматривать структуры информированности I_ij (структура информированности j -го агента в представлении i -го агента), I_ijk и т.д. Отождествляя структуру информированности с характеризуемым ею агентом, можно сказать, что, наряду с n реальными агентами (i-агентами, где 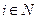)со структурами информированности I_i, в игре участвуют фантомные агенты ( 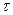-агенты, где 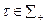, 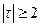) со структурами информированности 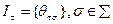. Фантомные агенты, существуя в сознании реальных агентов, влияют на их действия, о чем пойдет речь далее.

Определим фундаментальное для дальнейших рассмотрений понятие тождественности структур информированности.

Структуры информированност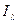и и 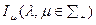называются тождественными если выполнены два условия

1) 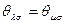для любого ;

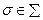2) последние индексы в последовательностях 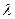и 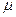совпадают.

Будем обозначать тождественность структур информированности следующим образом: .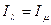

Первое из двух условий в определении тождественности структур прозрачно, второе же требует некоторых пояснений. Дело в том, что далее мы будем обсуждать действие 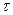-агента в зависимости от его структуры информированности 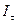и целевой функции f_i, которая как раз определяется последним индексом последовательности 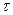. Поэтому удобно считать, что тождественность структур информированности означает в том числе и тождественность целевых функций.

Назовем 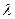-агента 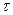-субъективно адекватно информированным о представлениях 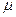-агента (или, короче, о 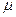-агенте), если

.

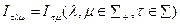Будем обозначать 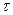-субъективную адекватную информированность 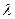-агента о 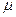-агенте следующим образом: .

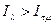Понятие тождественности структур информированности позволяет определить их важное свойство – сложность. Заметим, что наряду со структурой I имеется счетное множество структур 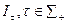, среди которых можно при помощи отношения тождественности выделить классы попарно нетождественных структур. Количество этих классов естественно считать сложностью структуры информированности.

Будем говорить, что структура информированности I имеет конечную сложность v=v(I), если существует такой конечный набор попарно нетождественных структур 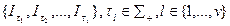, что для любой структуры 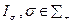, найдется тождественная ей структура 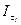из этого набора. Если такого конечного набора не существует, будем говорить, что структура I имеет бесконечную сложность: .

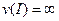Структуру информированности, имеющую конечную сложность, будем называть конечной (еще раз отметим, что при этом дерево структуры информированности все равно остается бесконечным). В противном случае структуру информированности будем называть бесконечной.

Ясно, что минимально возможная сложность структуры информированности в точности равна числу участвующих в игре реальных агентов (напомним, что по определению тождественности структур информированности они попарно различаются у реальных агентов).

Любой набор (конечный или счетный) попарно нетождественных структур 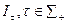, такой, что любая структура 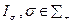, тождественна одной из них, называется базисом структуры информированности I.

Если структура информированности I имеет конечную сложность, то можно определить максимальную длину последовательности индексов 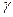такую, что, зная все структуры 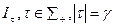, можно найти и все остальные структуры. Эта длина в определенном смысле характеризует ранг рефлексии, необходимый для описания структуры информированности.

Будем говорить, что структура информированности I, 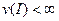, имеет конечную глубину 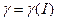, если:

1) для любой структуры 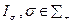, найдется тождественная ей структура ;

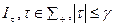2) для любого целого положительного числа 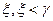, существует структура 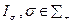, не тождественная никакой из структур .

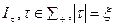Если 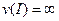, то и глубину будем считать бесконечной: .

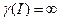Понятия сложности и глубины структуры информированности игры можно рассматривать 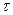-субъективно. В частности, глубину структуры информированности игры с точки зрения 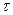-агента, 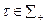, будем называть рангом рефлексии 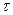-агента.

Граф рефлексивной игры. Если структура информированности имеет конечную сложность, то можно построить граф рефлексивной игры, наглядно показывающий взаимосвязь между действиями агентов (как реальных, так и фантомных), участвующих в равновесии.

Вершинами этого ориентированного графа являются действия 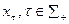, отвечающие попарно нетождественным структурам информированности 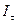, или компоненты структуры информированности 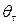, или просто номер 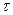реального или фантомного агента, .

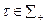Между вершинами проведены дуги по следующему правилу: к каждой вершине 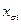проведены дуги от (n –1) вершин, отвечающих структурам 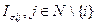. Если две вершины соединены двумя противоположно направленными дугами, будем изображать одно ребро с двумя стрелками.

Подчеркнем, что граф рефлексивной игры соответствует системе уравнений (6.6) (то есть определению информационного равновесия), в то время как решения ее может и не существовать.

Итак, граф G_I рефлексивной игры Г_I (см. определение рефлексивной игры выше), структура информированности которой имеет конечную сложность, определяется следующим образом:

1) вершины графа G_I соответствуют реальным и фантомным агентам, участвующим в рефлексивной игре, то есть попарно нетождественным структурам информированности;

2) дуги графа G_I отражают взаимную информированность агентов: если от одного агента (реального или фантомного) существует путь к другому агенту, то второй адекватно информирован о первом.

Если в вершинах графа G_I изображать представления соответствующего агента о состоянии природы, то рефлексивная игра Г_I с конечной структурой информированности I может быть задана кортежем 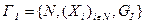, где N - множество реальных агентов, X_i - множество допустимых действий i -го агента, 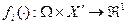- его целевая функция, 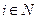, G_I - граф рефлексивной игры.

Отметим, что во многих случаях рефлексивную игру более удобно (и наглядно) описывать именно в терминах графа G_I, а не дерева информационной структуры (см. ниже примеры графов рефлексивных игр).