«Принцип дефицита». Книга американского психолога Р. Чалдини посвящена описанию и классификации стереотипов поведения, которым зачастую следуют люди, принимая те или иные решения. Эти стереотипы представляют собой некие «программы», которые «включаются» при определенных обстоятельствах и предопределяют действия человека, в том числе и явно иррациональные действия. Р. Чалдини выделяет шесть «фундаментальных психологических принципов, которые лежат в основе человеческого поведения»: принцип последовательности, принцип взаимного обмена, принцип социального доказательства, принцип авторитета, принцип благорасположения, принцип дефицита (здесь и далее до конца лекции будем ссылаться на работу Р. Чалдини). Остановимся на последнем из этих принципов.
Суть принципа дефицита состоит в следующем: «ценность чего-либо позитивного в наших глазах существенно увеличивается, если оно становится недоступным». В частности, это относится к дефицитной информации, причем «эксклюзивная информация является более убедительной. В качестве одного из подтверждений этого тезиса приводится следующий эксперимент, проведенный изучавшим психологию бизнесменом, владельцем компании, импортирующей в США говядину.
«Торговые агенты позвонили, как обычно, постоянным клиентам компании – закупщикам говядины для супермаркетов и других точек, торгующих продуктами в розницу, и одним из трех способов предложили им сделать заказ. Одни клиенты услышали предложение, сделанное в стандартной форме. Другим клиентам дополнительно была предоставлена информация о том, что поставки импортной говядины будут сокращены в ближайшие несколько месяцев. Третья группа клиентов получила те же сведения, что и вторая группа, а также информацию о том, что мало кто узнает о предстоящем сокращении поставок, так как эти сведения поступили из надежного, но засекреченного источника.
|
|
… По сравнению с клиентами, которым было сделано торговое предложение в стандартной форме, те клиенты, которым было также сказано о дефиците говядины, заказали ее в два раза больше… Клиенты, которые решили, что владеют «исключительной» информацией… приобрели в шесть раз больше говядины, чем клиенты, которым было сделано торговое предложение в стандартной форме. Очевидно, сообщение о том, что информация о дефиците сама является дефицитной, сделала данную информацию особенно убедительной».
Не подвергая сомнению справедливость выводов Р. Чалдини, попробуем взглянуть на ситуацию несколько по-иному и объяснить действия клиентов компании, исходя из теоретико-игровой модели.
Итак, пусть имеется n клиентов компании - далее будем называть их агентами - принимающих решение об объемах закупки говядины. Будем считать, что число агентов n достаточно велико, все агенты идентичны и конкурируют по Курно при линейной зависимости цены от предложения. Это означает, что целевые функции агентов выглядят следующим образом:
,
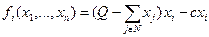где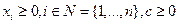 
. Содержательно, xi - объем продаж агента за рассматриваемый период времени, 
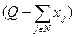- цена, которая при этом устанавливается на рынке, c - оптовая цена, по которой агенты закупают товар. Тогда первое слагаемое в целевой функции может интерпретироваться как произведение цены на объем продаж - выручка от продаж, а второе слагаемое - как затраты на закупку товара.
|
|
Дифференцируя целевые функции, приравнивая производные к нулю и решая получившуюся систему, можно найти равновесные действия агентов в условиях общего знания:
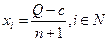, (6.16)
(по предположению все агенты идентичны, поэтому их равновесные действия одинаковы). Такова ситуация в отсутствии информационного воздействия. Агенты первого типа, которым было сделано предложение в стандартной форме, закупили товар в объеме (6.16), рассчитывая реализовать его в данный период времени.
Рассмотрим теперь поведение агентов второго типа, которым было сообщено, что поставки будут сокращены. Можно предположить, что они считали этот факт общим знанием. В таком случае для них рациональным действием было закупить в два раза больше товара, чтобы иметь возможность реализовать его в следующий период времени в том же равновесном количестве (6.16) (и одновременно заниматься поисками других поставщиков).
Наконец, рассмотрим поведение агентов третьего типа, которым было сообщено, что поставки будут сокращены и эта информация доступна лишь некоторому числу агентов. Для таких агентов, возможно, рационально предположить следующее. Существуют два типа агентов - неинформированные и информированные (инсайдеры), к которым агенты третьего типа относят себя. Неинформированные агенты в данном периоде будут реализовывать товар в объеме (6.16), а в следующем, не имея товара, прекратят участие в игре. Таким образом, число игроков в следующем периоде (равное числу инсайдеров) сократится с п до некоторого числа kn, k< 1, где k - доля инсайдеров. Тогда в следующем периоде равновесным будет действие:
|
|
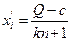. (6.17)
Сравнивая (6.16) и (6.17) легко видеть, что при больших п имеет место соотношение:
.
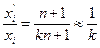Поэтому агенты третьего типа закупали товар в объеме (xi + x’i), т. е. в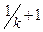 
раз больше, чем агенты первого типа. Если доля инсайдеров составляет, с точки зрения агентов третьего типа, пятую часть от общего числа агентов (то есть k= 1/5и этот факт субъективно является общим знанием), то получаем:
xi + x’i =6 хi.
В этом случае рациональным для агентов третьего типа является закупка в 6 раз большего объема товара, чем для агентов первого типа. Таким образом, при сделанных предположениях мы получаем именно тот результат, который описан в книге Р. Чалдини.
Аккордная оплата труда. Рассмотрим организационную систему, состоящую из центра и п агентов, осуществляющих совместную деятельность.
Стратегией i -го агента является выбор действия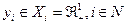 
,стратегией центра - выбор системы стимулирования, определяющей размер вознаграждения каждого агента в зависимости от результата их совместной деятельности. Предположим, что технология взаимодействия агентов такова, что для достижения требуемого результата необходимо, чтобы сумма их действий была не меньше заданной величины 
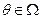. В этом случае i -й агент получает от центра фиксированное вознаграждение 
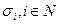,в случае же 
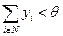вознаграждение каждого агента равно нулю.
Реализация действия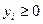 
требует от i -го агента затрат ci (y, ri), где ri> 0 - его тип (параметр, описывающий индивидуальные характеристики), 
.
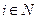Относительно функций затрат агентов предположим, что ci (y,ri) - непрерывная возрастающая по yi и убывающая по ri функция, причем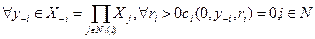 
.
Описанную модель взаимодействия будем далее называть игрой «Аккордная оплата труда». Определим множество индивидуально рациональных действий агентов:
.
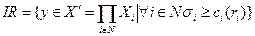Если затраты агентов сепарабельны, то есть затраты ci (yi,ri) каждого агента зависят только от его собственных действий и не зависят от действий других агентов, получаем, что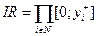 
,
где:
.
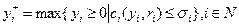Обозначим:
,
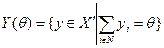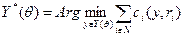
Рассмотрим последовательно различные варианты информированности агентов о значении параметра 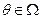. Как мы увидим, даже небольшое усложнение структуры информированности может существенно изменить множество информационных равновесий рассматриваемой рефлексивной игры.
Вариант I. Предположим, что значение 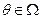является общим знанием. Тогда равновесием игры агентов является параметрическое равновесие Нэша, принадлежащее множеству:
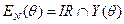. (6.18)
Определим также множество эффективных по Парето действий агентов:
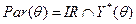. (6.19)
Так как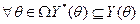 
,то из (6.18) и (6.19) следует, что множество эффективных по Парето действий является одним из равновесий Нэша. Но множество равновесий Нэша может оказаться шире - в частности, при 
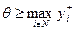оно всегда содержит вектор нулевых действий.
Пусть функции затрат агентов являются функциями затрат типа Кобба-Дугласа: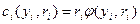 
, где 
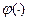- гладкая монотонно возрастающая выпуклая функция, удовлетворяющая равенству 
.
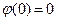Тогда эффективной по Парето является единственная точка: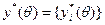 
, где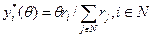 
.
Вычислим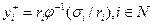 
, тогда при:
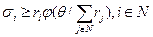. (6.20)
множество Парето не пусто.
Множества равновесий Нэша в игре п=2 агентов для двух значений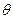 
: 
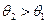приведены на рис. 6.10 (точка (0; 0) является равновесием Нэша в обоих случаях).
Итак, мы рассмотрели простейший вариант информированности агентов, соответствующий ситуации, когда значение параметра 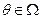является общим знанием. Рассмотрим следующий (в порядке возрастания сложности структуры информированности агентов) вариант информированности, в рамках которого общим знанием являются индивидуальные представления { 
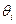} агентов о значении параметра .
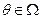Вариант II. Предположим, что представления агентов о неопределенном параметре попарно различны, но при этом являются общим знанием. Иными словами, имеет место асимметричное общее знание.
Не ограничивая общности, занумеруем агентов таким образом, чтобы их представления возрастали: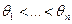 
. Структура возможных равновесий в этой ситуации описывается следующим утверждением.
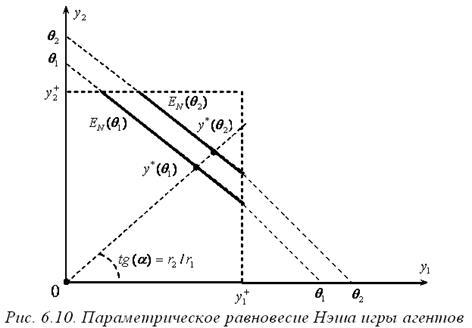
Утверждение 6.4. В игре «Аккордная оплата труда», для которо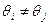й 
, при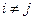 
, равновесными (в зависимости от соотношения между параметрами) могут быть следующие n +1 исходов:
; 
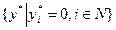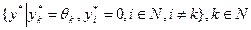. Содержательно это означает следующее: либо никто не работает, либо работает один k -йагент, выбирая действие 
.
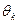Доказательство. Пусть вектор действий y*=(y 1*,…, yn * ) является равновесием (очевидно, при этом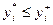 
для любого 
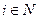). Пусть существует такое 
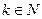, что yk * > 0. Покажем, что в этом случае 
.
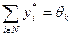Действительно, если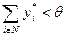 
, то k -йагент не рассчитывает на получение вознаграждения и, следовательно, может увеличить свой (субъективно ожидаемый) выигрыш с отрицательного до нулевого, выбрав нулевое действие. Если же 
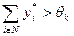, то k -йагент рассчитывает на получение вознаграждения, однако он может увеличить свой выигрыш, выбрав вместо 
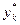действие 
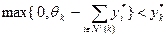. Таким образом, при 
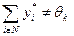k -й агент может увеличить свой выигрыш, что противоречит равновесности вектора y*.
Мы показали, что, если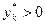 
, то 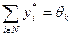. Но в силу условия 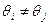, это равенство может выполняться лишь для одного 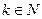. Поэтому если 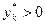, то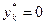 
для всех 
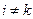. При этом, очевидно, 
. 
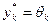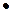
Рассмотрим теперь вопрос о том, при каких соотношениях между параметрами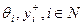 
, реализуется каждое из равновесий, перечисленных в формулировке утверждения 6.9. Вектор (0,…,0) является равновесным в случае, когда никакой i -й агент не может собственными усилиями выполнить достаточную (с его точки зрения) для получения вознаграждения работу (либо это усилие составляет в точности 
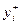, так что выигрыш i -го агента остается нулевым).
Это условие формально записывается следующим образом: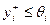 
для любого i. Вектор 
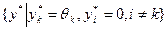является равновесным, если 
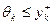, а все агенты с номерами i > k, считая, что вознаграждения не будет, являются недостаточно эффективными, чтобы собственными усилиями компенсировать величину 
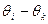. Формально: 
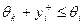для любого i > k.
Возможные равновесия в игре двух агентов изображены на рис. 6.11. Заметим, что, в отличие от варианта I, существует область, в которой равновесие отсутствует.
Рассмотрим теперь общий случай, когда представления агентов могут и совпадать: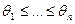 
. В этом случае может появиться целая область равновесий, аналогично варианту I. Пусть, например, выполняются соотношения 
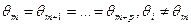при 
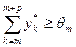. Тогда при выполнении условий 
и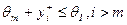 
, равновесным является любой вектор y*, для которого: 
, 
, 
; 
, .
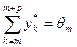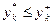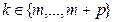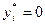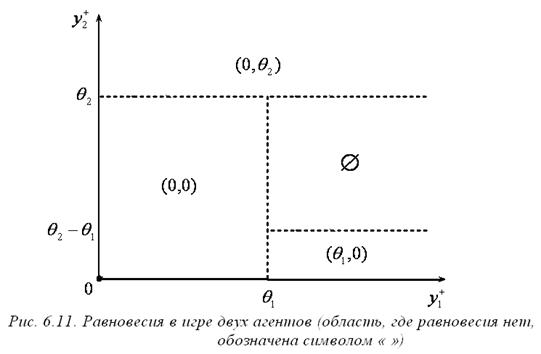
Содержательно это означает, что в равновесии всю работу выполняют агенты, которые одинаково представляют себе необходимый для получения вознаграждения объем работы.
Вариант III. Пусть теперь структура информированности игры имеет глубину 2, но каждый агент считает, что играет в игру с асимметричным общим знанием. В этом случае множество возможных равновесных ситуаций становится максимально возможным: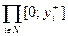 
. Более того, справедливо следующее утверждение.
Утверждение 6.5. В игре «Аккордная оплата труда» для любого вектора действий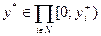 
существует такая структура информированности глубины два (при которой каждый агент субъективно играет в игру с асимметричным общим знанием), что вектор у * является единственным равновесием.
Доказательство. Достаточно для каждого 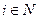положить
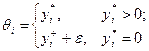
(здесь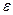 
- произвольное положительное число) и выбрать любые 
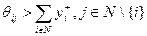. Тогда i -й агент ожидает от оппонентов нулевых действий, а его собственным субъективно равновесным действием является 
.
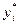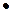
Замечание 1. Построенное в доказательстве утверждения 6.10 равновесие является (объективно) Парето-эффективным, если сумма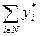 
равна истинному значению неопределенного параметра 
.
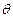Замечание 2. Действие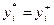 
является равновесным, если 
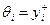. Однако, при этом равновесным будет и действие 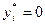- в обоих случаях субъективно ожидаемый i -м агентом выигрыш равен нулю.
Вариант IV. Пусть теперь структура информированности игры имеет глубину два, и на нижнем уровне имеется симметричное общее знание. Иными словами, каждый фантомный агент считает: неопределенный параметр равен 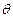, и это общее знание.
Оказывается, что и в этом случае множество равновесных ситуаций является максимально возможным: 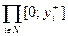. Более того, справедливо следующее утверждение.
Утверждение 6.6. В игре «Аккордная оплата труда» для любого вектора действий 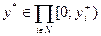существует такая структура информированности глубины два с симметричным общим знанием на нижнем уровне, что вектор у * является единственным равновесием.
Доказательство. Возьмем любое значение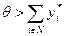 
и будем считать, что это значение является общим знанием среди фантомных агентов. Тогда единственным равновесием в игре фантомных агентов является выбор каждым из них нулевого действия.
Далее, для каждого 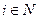положим:
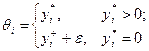
где 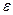- произвольное положительное число. Тогда, как нетрудно видеть, наилучшим ответом i -го агента на ожидаемые им нулевые действия оппонентов является выбор действия yi*.
Замечания 1 и 2, сделанные при анализе варианта III, можно повторить дословно и для варианта IV.
Таким образом, мы исследовали структуру информационных равновесий игры «Аккордная оплата труда» при различных вариантах информированности агентов. Полученные результаты полностью подтверждают интуитивно правдоподобный качественный вывод: в коллективе работников совместная работа возможна (является равновесной) лишь в том случае, когда имеется общее знание о том, какой объем работ необходимо выполнить для получения вознаграждения.
Рассмотрим теперь вопрос о стабильности информационного равновесия. Анализ проведем для варианта II, когда имеет место асимметричное общее знание. Будем считать, что в результате игры общим знанием среди агентов становится факт выплаты или невыплаты вознаграждения.
Равновесие (0, …, 0), очевидно, стабильно в любом случае: никто не работает, не ожидает получить вознаграждение и не получает его.
Равновесие вида 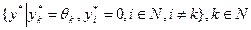, в случае 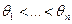возможно, как было показано выше, при 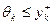, 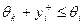для любого i>k. Тогда i -агенты с номерами 
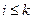ожидают выплаты вознаграждения, а с номерами i>k - не ожидают. Поэтому единственная возможность стабильности - условие k = n. Таким образом, получаем условие стабильности:
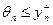(6.21)
Аналогично при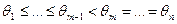 
стабильным является любой набор
.
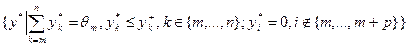В соответствии с утверждением 6.10, центр может при помощи информационного управления (в частности, путем формирования структуры, при которой каждый агент субъективно играет в игру с асимметричным общим знанием) добиться от агентов любого набора действий 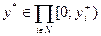. Оказывается, что существует и стабильное информационное управление, обеспечивающее этот результат. Покажем это для 
.
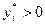Пусть задан набор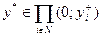 
, 
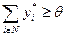. Положим для каждого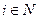 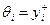и для каждого 
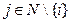возьмем любые 
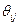, такие, что 
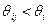. Тогда для i -агента субъективно выполнено условие стабильности (6.21) и 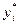- его единственное равновесное действие. При этом
1) работа будет выполнена, и агенты получат вознаграждение;
2) получение вознаграждения будет ожидаемым исходом для всех реальных и фантомных агентов.
Содержательно, ситуация при этом возникает следующая: каждый агент считает, что именно он выполнил всю работу и что это - общее знание.
Коррупция. Рассмотрим следующую теоретико-игровую модель коррупции. Пусть имеются п агентов - чиновников, дополнительный доход каждого из которых пропорционален сумме полученных им взяток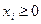 
, предложение которых будем считать неограниченным, 
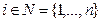. Пусть каждый из п агентов характеризуется своим типом 
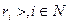, и тип агента достоверно ему известен, но не известен остальным агентам. Содержательно тип агента может интерпретироваться как субъективное восприятие им «силы» штрафов.
За коррупционную деятельность (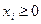), вне зависимости от ее размера, на агента может быть наложен штраф 
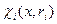, зависящий от действий 
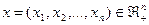всех агентов и типа данного агента.
Таким образом, целевая функция i -го агента имеет вид:
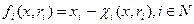. (6.22)
Относительно функции штрафов предположим, что она имеет вид:
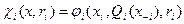. (6.23)
Содержательно предположение (6.23) означает, что штраф, накладываемый на i -го агента, зависит от его действия и от агрегированной обстановки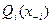 
(которая может интерпретироваться как «общий уровень коррумпированности остальных чиновников» с точки зрения i -го агента).
Предположим, что число агентов и общий вид целевых функций являются общим знанием, а относительно параметра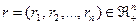 
каждый из агентов имеет иерархию представлений: rij - представление i -го агента о типе j -го агента, rijk - представление i -го агента о представлениях j -го агента о типе k- гоагента и т.д., 
.
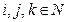Предположим также, что агенты наблюдают общий уровень коррумпированности. Поэтому стабильность информационного равновесия будет иметь место при любых представлениях о типах реальных или фантомных оппонентов, таких, что соответствующее информационное равновесие приводит к одному и тому же значению агрегата Qi (•) для любого .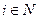
Тогда, как нетрудно видеть, для целевых функций агентов (6.22), (6.23) выполнены условия утверждения 6.8. Поэтому для любого числа агентов и любой структуры информированности все стабильные равновесия в рассматриваемой игре являются истинными. Таким образом, справедливо следующее
Утверждение 6.7. Пусть набор действий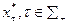 
, - стабильное информационное равновесие в игре (6.22), (6.23). Тогда это истинное равновесие.
Следствие. Уровень коррумпированности в стабильной ситуации не зависит от взаимных представлений коррупционеров о типах друг друга. При этом не важно, являются ли сами эти представления истинными или ложными.
Отсюда вытекает, что невозможно повлиять на уровень коррумпированности лишь путем изменения взаимных представлений. Поэтому любое стабильное информационное управление приводит к одному и тому же уровню коррумпированности.
Предположим, что:
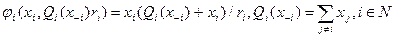, и все типы одинаковы: r 1=…= rn = r. Тогда, как нетрудно убедиться, равновесные действия агентов таковы: 
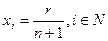, а общий уровень коррумпированности составляет 
.
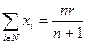Изменить последнюю величину можно, лишь повлияв непосредственно на типы агентов.
Биполярный выбор. Рассмотрим ситуацию, когда агенты из бесконечно большой «популяции» осуществляют выбор между двумя альтернативами, которые будем для общности называть позитивным и негативным полюсами. Это может быть кандидат на выборах (голосовать «за» или «против»), продукт или услуга (покупать или нет), этический выбор (поступить «хорошо» или «плохо») и пр.
В силу бесконечности числа агентов будем считать, что при решении задачи управления всей «популяцией» выбор каждого конкретного агента не играет роли, а важна доля агентов, выбирающих позитивный полюс. Иначе это можно сформулировать следующим образом: действием «агрегированного» агента является вероятность x выбора им позитивного полюса.
Примем следующие предположения:
1) существует n различных типов агентов;
2) доля агентов i -го типа составляет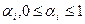 
;
3) действие агента i -го типа задается функцией реакции на ожидание:
,
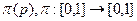где p - ожидаемая агентами вероятность выбора позитивного полюса произвольным агентом из «популяции». Иными словами, если агент ожидает, что доля выбравших позитивный полюс составляет p, то его действие xi определяется следующим образом:
.
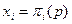4) пункты 1-3 являются общим знанием среди агентов.
Пусть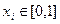 
- действие агента i -го типа. Тогда доля выбравших позитивный полюс составляет: 
.
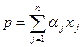Определим равновесие биполярного выбора как набор действий хi, удовлетворяющих системе соотношений:
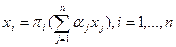. (6.24)
В качестве отступления заметим, что соотношения (6.24) являются одной из возможностей описания биполярного выбора. Другие возможные подходы обсуждаются, например, в работах В.А. Лефевра, ТА. Таран и др. В этих работах предполагается, что принимающий решение агент осуществляет рефлексию первого рода, т.е. занимает позицию наблюдателя по отношению к своему поведению, своим мыслям и чувствам. Иными словами, в нем существует несколько соотнесенных друг с другом уровней, а итоговое решение определяется как влиянием внешней среды, так и состоянием этих уровней. В данной же работе агент понимается как индивид, т.е. «неделимый», и осуществляет рефлексию второго рода - относительно принятия решений оппонентами.
Вернемся к обсуждению равновесия биполярного выбора. Заметим, что выражения (6.24) задают отображение единичного гиперкуба [0, 1] n на себя:
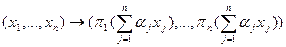. (6.25)
Если функции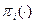 
непрерывны (что представляется довольно естественным предположением), то и отображение (6.25) непрерывно. Тогда по теореме о неподвижной точке у системы (6.24) имеется хотя бы одно решение.
Приведем пример. Пусть существуют агенты трех типов (n =3), действия которых определяются следующими функциями:
.
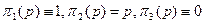Содержательно: агенты первого типа независимо ни от чего выбирают позитивный полюс, агенты третьего типа - негативный. Что касается агентов второго типа, то они колеблются, и их действия совпадают с ожидаемым действием «популяции» в целом.
Система (6.24) в данном случае сводится к соотношениям:
,
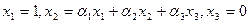откуда (здесь и далее полагаем, что 0< ai <1, i =1, 2, 3):
.
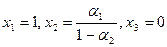При этом:
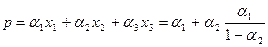. (6.26)
Предположим теперь, что некий управляющий орган – центр – имеет возможность повлиять на ситуацию и стремится увеличить вероятность позитивного выбора в «популяции» в целом (т.е. величину p). Для этого центр может повлиять на агентов второй либо третьей группы (агенты первой группы и так выбирают x 1 = 1). Пусть центр может повлиять на третью группу, переведя долю y ее членов во вторую и затратив некий ресурс (например, финансовый) в объеме C 2 y. Центр может также повлиять на вторую группу, изменив представления ее членов об a 3 (независимо от фактического значения этого параметра). Именно, влияние состоит в формировании у второй группы следующего представления: «доля x членов третьей группы перешли во вторую». Затраты на формирование такого представления составляют C 1 x.
Иными словами, центр может изменить либо реальную, либо «фантомную», воображаемую долю агентов третьего типа. При этом совокупный ресурс (бюджет), которым располагает центр, составляет C.
Задача центра состоит в следующем: распределить ресурс C (т.е. выбрать доли x и y) таким образом, чтобы вероятность p была максимальной. Формально оптимизационная задача центра ставится следующим образом (см. (6.26)):
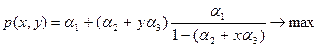(6.27)
при ограничениях:
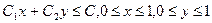. (6.28)
Легко видеть, что задача (6.27) сводится к максимизации функции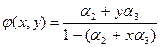 
, которая возрастает по обоим аргументам x и y, поэтому первое из ограничений (6.28) обращается в равенство. Итак, задача свелась к нахождению максимума функции
.
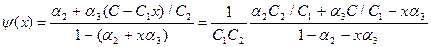Нетрудно видеть, что функция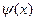 
является монотонно возрастающей (соответственно, монотонно убывающей или константой), если выражение:
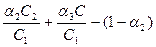(6.29)
положительно (соответственно, отрицательно или равно нулю).
Введем обозначения: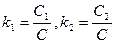 
. Тогда условие положительности выражения (6.29) запишется в виде:
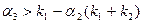. (6.30)
Далее будем предполагать, что C 1> C и C 2> C. Содержательно это означает, что у центра не так много ресурсов, чтобы всех агентов третьего типа «превратить» в агентов второго типа. При этом оптимальным будет такой выбор центра, когда весь ресурс вкладывается в увеличение либо реальной, либо воображаемой (при выполнении (6.30)) доли агентов второго типа.
Зависимость оптимального выбора центра от параметров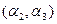 
изображена на рис. 6.12.
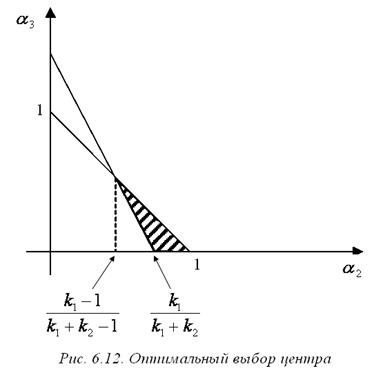
На рис. 6.12 заштрихована область, где выполнено условие (6.30), т.е. оптимально для центра весь ресурс направить на изменение представлений:
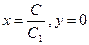. (6.31)
Решение (6.31) отвечает ситуации, когда доля a 2 агентов второго типа достаточно велика. Из рис. 6.12 видно, что если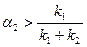 
, то решение (6.31) всегда оптимально. Если же:
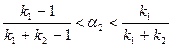, (6.32)
то решение (6.31) оптимально при достаточно больших a 3. Содержательно последний случай означает следующее: при некотором диапазоне значений параметра a 2 (т.е. при выполнении (6.32)) оптимально влиять на представления, когда они слишком пессимистичны (т.е. когда a 3 достаточно велико и, следовательно, велика вероятность p выбора негативного полюса).
В заключение отметим, что рассмотрен простейший случай информационного управления в условиях биполярного выбора. Дальнейшее развитие модели (увеличение числа типов агентов, усложнение структуры информированности, усложнение функций реакции на ожидание) и ее сопоставление с наблюдаемыми результатами действий экономических (покупатели) и политических (избиратели) агентов представляется перспективным направлением дальнейших исследований.
Реклама товара. В настоящем подразделе рассматриваются модели информационного управления, осуществляемого средствами массовой информации (СМИ), на примере рекламы и предвыборных технологий.
Предположим, что имеется агент – объект информационного воздействия. Цель воздействия – сформировать у агента определенное отношение к конкретному объекту или субъекту.
В случае рекламы агентом является потребитель, а объектом – товар или услуга. Требуется, чтобы потребитель приобрел данный товар или услугу.
В случае предвыборных технологий агентом является избиратель, а субъектом – кандидат. Требуется, чтобы избиратель проголосовал за данного кандидата.
Рассмотрим i -го агента. Всех остальных агентов объединим в одного, для обозначения которого будем использовать индекс j. Пусть 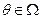– объективная характеристика объекта, неизвестная достоверно ни одному из агентов. В качестве характеристик могут выступать потребительские свойства товаров, качества кандидатов и т.д.
Обозначим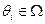 
– представления i -го агента об объекте, 
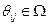– его представления о представлениях об объекте j -го агента, и т.д.
Предположим для простоты, во-первых, что множество возможных действий каждого агента состоит из двух действий: Xi=Xj={a; r }, где действие a (accept) соответствует приобретению товара или услуги, голосованию за рассматриваемого кандидата и т.д., а действие r (reject) - отказу от приобретения товара или услуги, голосованию за других кандидатов и т.д. Во-вторых, предположим, что множество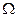 
состоит из двух элементов, характеризующих качества объекта - g (good) и b (bad), то есть 
.
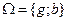Рассмотрим последовательно (в порядке усложнения) ряд моделей поведения агента.
Модель 0 (рефлексия отсутствует). Предположим, что поведение рассматриваемого агента описывается отображением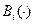 
множества 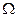свойств объекта во множество Xi действий агента, то есть Bi: 
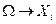. Примером такого отображения может служить следующее: Bi(g)=a, Bi(b)=r, то есть если агент считает, что товар (кандидат) хороший, то он его приобретает (отдает за него свой голос), и отвергает в противном случае.
В данной модели информационное управление заключается в формировании у агента представлений об объекте, приводящих к требуемому выбору. В рассматриваемом примере для того, чтобы агент приобрел товар (проголосовал за требуемого кандидата), необходимо сформировать у него следующие представления: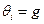 
. (