Базовая модель теории контрактов

Рассмотрим организационную систему, состоящую из центра и одного агента. Центр продает агенту некий товар в количестве q за сумму t. Функция полезности центра 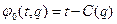. Функция C (q) – стоимость производства товара для центра – дважды дифференцируемая выпуклая функция, C’ (0)=0, C’ (∞)=∞. Функция полезности агента 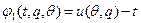. 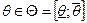– положительный параметр, тип агента. Функция 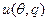– полезность товара для агента – возрастает и вогнута по q и возрастает по .

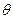Центру известно множество 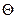и вероятностное распределение типа агента на этом множестве, причем интегральная функция распределения 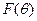дифференцируема - .

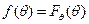Задача центра - максимизировать свою ожидаемую полезность:

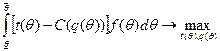
На основании принципа выявления строится неманипулируемый механизм - «меню» контрактов 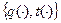, зависящий от сообщаемой агентом оценки своего типа. (Принцип выявления – западный аналог принципа открытого управления (см. выше). Для систем с одним агентом эти принципы эквивалентны).

Необходимые условия неманипулируемости механизма имеют следующий вид:

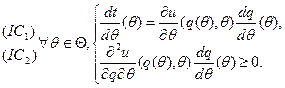
При выполнении условий Спенса-Мирлиса:

,

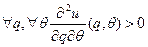доказано, что функция 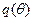является неубывающей функцией своего аргумента.

Предполагается, что 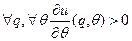. Вводится функция прибыли агента при использовании оптимального неманипулируемого механизма в зависимости от его типа - 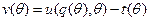.Причем, при выполнении условия IC ₁, 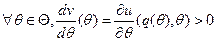. Поэтому, выполнение условий индивидуальной рациональности агента 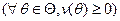может быть обеспечено следующим образом 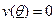, из чего следует, что: 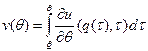, и .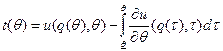

Задача центра (построение механизма, максимизирующего его прибыль) сводится к решению следующего уравнения:

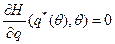
при условии

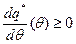б (5.3)

где .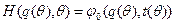

Возможны два случая: ограничение (5.3) выполняется всюду как строгое неравенство или при некоторых 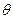ограничение (5.3) выполняется как равенство.

Первый случай очень прост: множитель Лагранжа при ограничении (5.3) равен нулю и 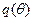определяется из условия 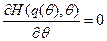, то есть:

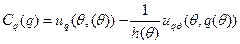, (5.4.)

где .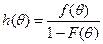

Каждый тип агентов получает свой контракт (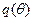 строго возрастает по 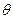). Таким образом, все типы, кроме самого высокого, получают уровень q меньше оптимального, а самый высокий тип получает эффективное количество.

Если же хотя бы при некоторых 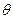в ограничение (5.3) выполняется как равенство, ситуация гораздо сложнее. Для решения задачи нужно использовать принцип максимума Понтрягина. Рассмотрим динамическую задачу максимизации:

,

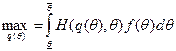где θ - аналог времени, q - фазовая переменная, изменяющаяся по закону 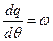, а 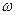– управление, ограниченное снизу: .

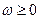Как правило, задачу решают следующим образом. Сначала предполагают, что контракт разделяющий, и вычисляют 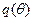из (5.4). Если полученная функция 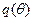не убывает, то задача решена, оптимальный контракт разделяющий. Если же полученная функция имеет убывающие участки, но необходимо решать изложенную выше задачу оптимального управления. При этом некоторые агенты с различными типами получат одинаковые контракты, то есть рав­новесие частично смешивающее.

Пример 5.4. Пусть 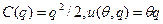,а тип агента распределен равномерно на множестве допустимых значений -

.

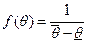Тогда получаем, что

,

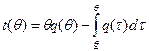а 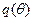определяется из решения уравнения 5.4:

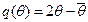
С учетом требований 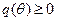- покупателю может продаваться лишь положительное количество товара получаем следующее меню контрактов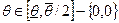: для , для :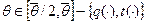

,

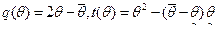где .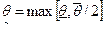

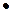
Итак, стандартная модель теории контрактов, рассмотренная выше, может быть применена для формирования гибкой шкалы цен на товар производителя - монополиста. Выставляя на продажу различные модификации своей продукции по различным ценам (что и является тем самым «меню» контрактов) производитель охватывает различные группы пользователей. Классический пример такого товара - вино. Чем дольше срок его выдержки, тем выше качество вина. Ценители вина готовы покупать более качественное вино по более высокой цене, неискушенные потребители готовы довольствоваться менее качественным продуктом по более низкой цене.

Используя модель теории контрактов, производитель может оптимизировать свой ожидаемый доход от продажи своего товара.

Но, варьироваться может не только качество товара, но и его объем. Чем большее количество товара приобретает покупатель, тем ниже его удельная стоимость. Зависимость цены товара от приобретаемого количества и является тем самым меню контрактов, которое может быть получено с помощью стандартной модели теории контрактов. Основной проблемой, возникающей при решении практических задач, является идентификация понятия типа покупателя и возможных пределов его значений.

Конкурсные механизмы

Непрерывные конкурсы. При обсуждении механизмов обратных приоритетов подчеркивалось, что ресурс распределяется пропорционально эффективности 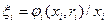его использования агентами. В конкурсном механизме ресурс получают только победители конкурса (на всех агентов ресурса может не хватить).

Предположим, что агенты сообщают центру две величины: заявку на ресурс s_i и оценку 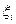ожидаемой эффективности его использования. Ожидаемый эффект для ОС в целом от деятельности i -го агента в этом случае равен: 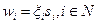. Упорядочим агентов в порядке убывания эффективностей: .

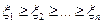Понятно, что агенты могут наобещать золотые горы, лишь бы получить финансирование. Поэтому при использовании конкурсных механизмов центр должен организовать действенную систему контроля за выполнением взятых обязательств. Введем систему штрафов: , пропорциональных отклонению ожидаемой эффективности 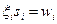от реальной - 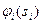. Отметим, что величина 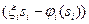характеризует обман, на который сознательно идет агент ради победы в конкурсе.

Целевая функция агента имеет вид:

,

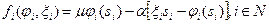где 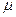- доля эффекта, остающаяся в распоряжении агентов (то есть 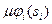- его доход). Отметим, что агент штрафуется только в случае, если 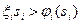. Если реальная эффективность оказалась выше ожидаемой, то штрафы равны нулю.

Ресурс R, имеющийся в распоряжении центра, распределяется следующим образом: первый агент (агент, имеющий максимальную эффективность) получает ресурс в запрашиваемом объеме s₁. Затем получает ресурс (в объеме s₂) агент с меньшей (второй по величине) эффективностью и так далее, пока не закончится весь ресурс. То есть центр раздает ресурс в требуемом объеме в порядке убывания эффективностей до тех пор, пока не закончится ресурс. Агенты, получившие ресурс в полном объеме, называются победителями конкурса. Существенным при этом является то, что некоторые агенты (например, последний (в упорядочении по эффективности) из победителей конкурса) могут получить ресурс не в полном объеме и, тем не менее, принести определенный эффект. Поэтому рассматриваемые конкурсы называются непрерывными.

Отметим, что при использовании такой процедуры победа в конкурсе зависит только от величины эффективности 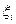и не зависит от величины заявки s_i. Поэтому агенты будут стремиться максимизировать свои целевые функции, то есть закажут такое количество ресурса, чтобы в случае победы значение их целевой функции было максимально.

Обозначим m – максимальный номер агента, победившего в конкурсе (то есть победителями являются агенты с номерами 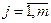). Нетрудно показать, что все победители сообщат одинаковые оценки эффективности, то есть 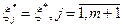. Более того, при достаточно общих предположениях о функциях штрафов конкурсные механизмы обеспечивают оптимальное распределение ресурса.

Дискретные конкурсы. Наблюдаемая в настоящее время распространенность, если не сказать «мода», использования на практике всевозможных конкурсов, а также приводимые для обоснования их целесообразности качественные рассуждения наталкивают на мысль – быть может честное соревнование действительно является панацеей от многих, если не всех, бед. На самом деле, формальный анализ конкурсных механизмов (которые в случае неделимых объектов конкурса называются тендерами, или дискретными конкурсами) показывает, что не все так просто.

Более корректно тендером (дискретным конкурсом) называется конкурс, в котором победители получают в точности заявленную величину (ресурса, финансирования, выгодный проект и т.д.), а проигравшие не получают ничего. Эффективность участника определяется как отношение оценки социально-экономического эффекта (известной, например, в результате объективной экспертизы) к сообщенной участником оценке (требуемого ресурса, затрат и т.д.). Основная идея простых конкурсов заключается в упорядочении участников в порядке убывания эффективностей и выделения им ресурса в требуемом объеме последовательно, пока не закончится весь ресурс. Победителями конкурса являются участники, получившие ресурс. К сожалению, гарантированная эффективность простых конкурсных механизмов равна нулю (точнее - может быть сколь угодно мала).

Несколько лучше обстоит дело в прямых конкурсных механизмах, в которых организатор конкурса, используя сообщенные оценки, решает задачу о ранце (ищет оптимальную с точки зрения суммарного эффекта комбинацию победителей) - гарантированная эффективность прямых конкурсов равна 0,5.