Для представления цифровых величин используются не только цифры натурального ряда, наиболее широко распространенные для традиционных величин. В XIII веке итальянский математик Леонардо Фибоначчи из Пизы, наблюдая закономерности увеличения численности биологических популяций, открыл интересную числовую последовательность, названную его именем [2].
Действительно, если в отличие от натурального ряда, в котором каждое последующее слагаемое образуется путем увеличения предыдущего элемента на единицу: 0, 1, 2, 3… и т.д., то в ряду Фибоначчи каждый последующий элемент есть сумма двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т.д. Однако более интересное заключается в том, что отношение двух соседних элементов ряда при возрастании их номера до бесконечности имеет предел:
. (1.1)
Выражение (1.1) определяет значение «золотой» пропорции - τ≈1,618, получившей практически «культовое» значение при развитии ремесел, искусства и науки особенно в средние века.
Однако долгое время после открытия числа ряда Фибоначчи рассматривались только как экзотические последовательности и мало использовались при исследованиях и в технике.
В начале 20-х годов прошлого века после появления основополагающих работ Норберта Винера по кибернетике, интерес к системам счисления стал возрастать. Применительно к вычислительной технике это привело к тому, что предпочтение долгое время отдавалось двоичной системе.
В начале 30-х годов 20-го столетия швейцарский исследователь Э. Цекендорф предложил систему счисления на основе чисел Фибоначчи:
N=anFn + an-1Fn-1 + …+ aiFi +…+ a1F1, где ai є{0, 1}- двоичная цифра i -разряда, Fn -числа Фибоначчи:
|
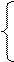
. (1.2)
В формуле (1.2) представлено фактическое определение чисел Фибоначчи. Однако наиболее «революционным» оказалось предложение в 1957г. американским математиком Дж. Бергманом. Им была предложена новая система τ-счисления:
A = anτn + an-1τn-1 +…+ aiτi +…+ a1τ1 =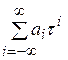 
, iє{0, ±1, ±2…}, (1.3)
где 
. На первый взгляд кажется, что система счисления Дж. Бергмана по определению-(1.3) не представляет ничего особенного, по сравнению с обычным позиционным кодированием. Но вся суть состоит именно в том, что основным элементом при построении чисел берется вещественное число τ, которое одновременно является корнем алгебраического уравнения х2-х-1=0 и обладает следующим замечательным свойством: τn = τn-1 + τn-2, n=0, ±1, ±2…. С помощью таких определений, частный случай которых – система счисления Бергмана, можно представить все другие числа, включая натуральные, дробные и иррациональные.
Коды Фибоначчи и «золотой пропорции» можно рассматривать как некоторое обобщенное классическое двоичное счисление. Для представления числа в них используются те же двоичные символы 0 и 1, образующие запись кода. Различие между ними возникает на этапе интерпретации весов разрядов. Например,
1001101 есть:
26 + 23 + 22 + 20 = 45– в двоичном коде;
13 + 3 + 2 + 1 = 19 – в коде Фибоначчи;
τ6 + τ3 + τ2 + τ0 = А – вещественное число в τ- коде.
Т.е. в τ - коде можно представлять иррациональные числа в виде конечной совокупности битов.
Особенностью кодов Фибоначчи является их естественная «избыточность», которая и используется для контроля преобразования информации в компьютерах. Например, число 19 в кодах Фибоначчи имеет и другие представления
19 =
= 1001101 =
= 1010001 = «минимальная» форма
= 0111101 = «максимальная» форма
Как видно из примера различные кодовые последовательности одного и того же числа могут получаться с помощью специальных операций «свертки»- (011→100) и «развертки»-(100→011). В этих операциях две рядом расположенные единицы заменяются нулями и наоборот.
Если над кодовой последовательностью выполнить все возможные свертки, то получится так называемая «минимальная» форма кодового изображения (отсутствие двух рядом стоящих единиц). Если осуществлять все развертки, то получиться «максимальная форма», в которой не встречается рядом двух нулей. Обе формы могут существовать в единственном числе.
Это свойство используется при проектировании так называемых «самопроверяющихся» компьютеров – «компьютеров Фибоначчи». Известно, что компьютеры, использующие двоичную систему счисления, не являются абсолютно надежными. Действительно, вовремя обнаружить перемену места 0 и 1 в 64-разрядном двоичном числе – задача очень трудная. Для нахождения таких ошибок приходится добавлять алгоритмы подсчета контрольных сумм, что сказывается на быстродействии программ в целом.
Другое дело – коды Фибоначчи. Здесь переход 0 в 1 и обратно сразу вызывает необходимость проведения операций свертки и развертки. Поэтому компьютеры Фибоначчи называют еще «самосинхронизующимися» компьютерами.
Существенным свойством системы счисления, особенно с позиций «информационной эпохи», является степень ее пригодности для конструирования вычислительных машин. При этом кроме простоты осуществления арифметических операций важно учитывать то, что называется «экономичностью» системы. Под этим понимается тот запас чисел, которые можно записать в данной системе с помощью определенного количества знаков.
Поясним это на примере. Чтобы в десятичной системе записать 1000 чисел (от 0 до 999), необходимо тридцать знаков (по десять цифр для каждого разряда). А в двоичной системе можно с помощью тридцати знаков записать 
различных чисел (так как для каждого двоичного разряда нужны только две цифры 0 и 1, то с помощью 30 цифр можно записывать числа, содержащие до 15 двоичных разрядов). Но >1000. Поэтому, имея 15 двоичных разрядов, можно записать больше чисел, чем с помощью трех десятичных разрядов. Таким образом, двоичная система более экономичная, чем десятичная.
Но какая из систем счисления самая экономичная? Невероятно, но ответить на этот вопрос можно, решив вполне конкретную задачу [3]. Пусть имеется 60 знаков. Можно, разбив их на 30 групп по два элемента в каждой, записать с их помощью в двоичной системе любое число, имеющее не более тридцати двоичных разрядов, т.е. в обще сложности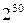 
чисел. Те же 60 знаков можно разбить на группы по три элемента и, пользуясь троичной системой счисления, записать 
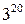различных чисел. Далее, разбив 60 знаков на 15 групп по 4 элемента в каждой, можно применить четверичную систему и записать 
чисел и т.д. В частности, воспользовавшись десятичной системой (т.е. разбив все знаки на шесть групп по 10 элементов в каждой), можно записать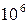 
чисел, а, применив шестидесятеричную (вавилонскую систему), можно с помощью шестидесяти знаков записать шестьдесят чисел.
Посмотрим, какая из возможных здесь систем самая экономичная, т.е. позволяет записать с помощью данных 60 знаков наибольшее количество чисел. Иными словами, речь идет о том, какое из чисел:
,
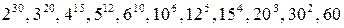наибольшее. Легко проверить, что наибольшим здесь будет число 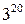. Действительно, покажем сначала, что:
.
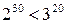Так как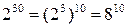 
, 
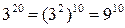, то наше неравенство можно переписать в виде:
.
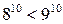Но в такой форме оно очевидно. Далее:
.
Следовательно, в силу уже доказанного,
.
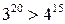Точно также легко проверить и справедливость следующей цепочки неравенств.
Таким образом, троичная система оказалась самой экономичной. Двоичная и равносильная ей, в смысле экономичности, четверичная система несколько уступают троичной, но превосходят все остальные системы.
Этот вывод никак не связан с тем, что рассматривалось именно шестьдесят знаков. Этот пример приведен только потому, что 60 знаков удобно разбивать на группы по 2, 3, 4, 5, и т.д. знаков.
В общем случае, если взять 
знаков, а за основание положить число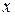 
, то получится 
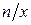разрядов, и количество чисел, которое при этом можно записать, будет равно:
.
Если рассмотреть это выражение, как функцию переменной х, то можно найти то значение х, при котором эта функция достигает максимум. Несложно показать, что оно равно 
- иррациональному числу, представляющему собой основание так называемых «натуральных» логарифмов и выполняющему важную роль в других разделах математики и обширных прикладных областях. Ближайшее к целое число есть 3. Оно и служит основанием наиболее экономичной системы счисления.
В середине прошлого века в Советском Союзе в МГУ Николаем Петровичем Брусенцовым был построен первый в мире компьютер на троичной системе счисления под названием «Сетунь». Основа его построения – логический элемент с тремя устойчивыми состояниями (0, 1, 2) на магнитных элементах [2].
I.2.3. Статистическая мера информации
При вероятностном подходе информация рассматривается как сообщения об исходе случайных событий, реализации случайных величин и функций, а количество информации ставится в зависимость от априорных вероятностей этих событий, величин, функций. Из опыта известно, что сообщение о часто встречающихся событиях, вероятность появления которых стремиться к 1, то есть к показателю полной достоверности, является малоинформативным. Столь же малоинформативным является сообщение о противоположном событии.
События можно рассматривать как возможные исходы некоторого опыта, причем все исходы составляют ансамбль в виде полной группы событий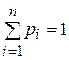 
.
Вообще событиями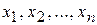 
могут быть n возможных дискретных состояний какой-либо физической системы, т.е. при этом выполняется соотношение, имеющее «нормирующий» характер 
.
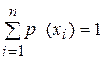В материальных системах неопределенность каждой ситуации характеризуется энтропией. Понятие энтропии имеет очень широкое толкование и распространяется на многие области знания [1, 9].
Так энтропия в термодинамике означает вероятность теплового состояния вещества, в математике – степень неопределенности ситуации в абстрактной задаче, в информатике она характеризует способность источника отдавать информацию. Однако все эти понятия родственны между собой и в общем случае отображают степень богатства и неожиданности состояния.
В статистической теории информации (теории связи), предложенной К.Шенноном в 1946г., энтропия количественно выражается как средняя функция множества вероятностей каждого из возможных исходов опыта:
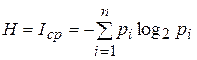. (1.4) В случае равновероятных исходов возможных событий, как следует из формулы (1.4), оценки количеств информации по Хартли и по Шеннону совпадают, что свидетельствует о полном использовании информационной емкости системы.
Количество информации только тогда равно энтропии, когда неопределенность ситуации снимается полностью. В общем случае нужно считать, что количество информации есть уменьшение энтропии вследствие опыта. Если неопределенность снимается полностью, то информация равна энтропии: I=H.
В случае неполного разрешения имеет место частная информация, являющаяся разницей между начальной и конечной энтропией: I=H1-H2
Наибольшее количество информации получается тогда, когда полностью снимается неопределенность, причем эта неопределенность была наибольшей – вероятности всех событий были одинакова. Это соответствует максимально возможному количеству информации, оцениваемому мерой Хартли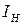 
:
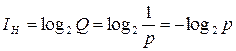. (1.5)
Q – число событий, p – вероятность их реализации в условиях равноопределенности. Таким образом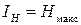 
.
Абсолютная избыточность информации D абс представляет собой разность между максимально возможным количеством информации и энтропией: D абс = 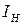- H = H макс – H. Пользуются также понятием относительной избыточности.