При использовании структурных мер учитывается только дискретное строение данного информационного комплекса. Значит, интересуются в особенности количеством содержащихся в нем информационных элементов, связями между ними или комбинациями из них.
Под информационными элементами понимаются неделимые части (кванты) информации в дискретных моделях реальных информационных комплексов.
В структурной теории различаются: геометрическая, комбинаторная и аддитивная меры информации.
Геометрическая мера. Определение количества информации геометрическим методом сводится к измерению элементов формы (длины линии, площади или объема геометрической модели) данного информационного комплекса в количестве дискретных единиц.
Геометрической мерой определяется потенциальное, то есть максимально возможное количество информации в заданных структурных габаритах. Это количество принято называть информационной емкостью исследуемой части информационной системы.
Предположим, например, что информация отражается полным комплексом XTN. Если дискретные отсчеты осуществляются по осям X, T и N соответственно через интервалы Δ X, Δ T и Δ N, то непрерывные координаты раскладываются на элементы (кванты), количество которых составляет: 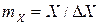 ;
; 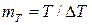 ;
; 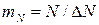 .
.
Тогда количество информации в полном комплексе 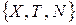 , определяемое геометрическим методом, равно: M = mX ·mT ·mN.
, определяемое геометрическим методом, равно: M = mX ·mT ·mN.
В общем случае дискретизация по осям пространства может быть неравномерной, а сами процессы могут изменяться во времени (нестационарны). Тогда количество информации следует определять по более сложным формулам, следующим из вариативного характера дискретизации.
Комбинаторная мера. К комбинаторной мере целесообразно прибегать тогда, когда требуется оценка возможности передачи информации при помощи различных информационных элементов. Вообще образование комбинаций есть одна из форм кодирования информации.
Количество комбинаций в комбинаторной мере вычисляется как количество комбинаций элементов. Таким образом оценке подвергается свойство потенциального структурного многообразия информационных комплексов. Сочетания из n элементов по m различаются неодинаковым составом элементов. Их возможное число (при n ≥ m) равно:
 .
.
Сочетания с повторениями также различаются составом элементов, но элементы могут в них повторяться до “ m ” раз. Их число равно:
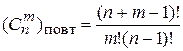 .
.
Перестановки h элементов различаются только их порядком. Число возможных вариантов равно: 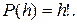
Перестановка с повторениями элементов, причем один из элементов повторяется α раз, другой β раз, и, наконец, последний γ раз, характеризуется возможным числом вариантов:
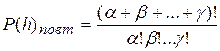 ,
,
где: α+ β +…+γ=h.
Размещения из h элементов по m различаются и по составу элементов и по их порядку. Возможное число размещений:
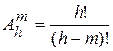 .
.
Возможное число размещений с повторениями до m раз из h элементов есть:  .
.
При использовании комбинаторной меры количество информации Q совпадает с числом возможных соединений (связей) между элементами. То есть при этом оценивается, в отличие от геометрической меры, не только число квантов, а их структурное многообразие.
Количество информации при том же числе элементов теперь многократно увеличивается.
Так, например, в случае простых сочетаний из 10 элементов по 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 элементов получается следующее количество вариантов, являющееся «идеальной» мерой количества информации:

Перестановки тех же 10 элементов дают: P (10)=10!=3626800.
Размещение 10 элементов по 10 различным позициям дают: Q= 1010 образований. Конечно, не всегда все возможные комбинации составляют действительные степени свободы рассматриваемой системы.
Аддитивная мера (мера Хартли). В теории информации важную роль играют комбинаторные схемы для чисел и кодов. Для иллюстрации введем понятие глубины h и длины l числа.
Глубиной h числа называется количество различных элементов (знаков), содержащееся в принятом алфавите. Глубина числа соответствует основанию системы счисления или кодирования. Один полный алфавит занимает одно числовое гнездо, глубина которого равна h. Используем в качестве геометрической модели схему, представленную на рис. 1.7.
 |
Рис. 1.7.
На схеме массива десятизначных дискретных чисел (n = l = h =10) в каждый данный момент реализуется только один какой-либо знак из h возможных. На геометрической модели реализация знака принимает форму выставления в первый ряд нужного знака из глубины гнезда, в котором в определенном порядке хранятся все нужные знаки.
На схеме массива десятизначных дискретных чисел (n = l = h =10) в каждый данный момент реализуется только один какой-либо знак из h возможных. На геометрической модели реализация знака принимает форму выставления в первый ряд нужного знака из глубины гнезда, в котором в определенном порядке хранятся все нужные знаки.
Длиной l называется количество числовых гнезд необходимых и достаточных для представления чисел нужной величины. Один набор из числовых гнезд образует одну числовую гряду, способную представить и хранить одно полное число длиной l. Некоторое количество чисел n представляется числовым полем.
При глубине h и длине l количество чисел, которое можно представить с помощью числовой гряды, выразится формулой: 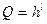 , то есть емкость гряды экспоненциально зависит от длины числа l. Вследствие показательного закона зависимости Q от l, число Q не является удобной мерой для оценки информационной емкости. Поэтому Хартли предложил ввести аддитивную, двоичную логарифмическую меру, позволяющую вычислить количество информации в двоичных единицах «битах». То есть I= log 2Q=l log 2h (бит). I – количество информации но Хартли. Если количество разрядов (длина l числа) равно 1 (h =2), то 1 log 2 2 =1 бит. Это и есть единица информации в принятой системе. Она соответствует одному элементарному событию, которое может произойти или не произойти. Помимо битов применяются единицы: ниты (натуральный логарифм) и диты (десятичный логарифм).
, то есть емкость гряды экспоненциально зависит от длины числа l. Вследствие показательного закона зависимости Q от l, число Q не является удобной мерой для оценки информационной емкости. Поэтому Хартли предложил ввести аддитивную, двоичную логарифмическую меру, позволяющую вычислить количество информации в двоичных единицах «битах». То есть I= log 2Q=l log 2h (бит). I – количество информации но Хартли. Если количество разрядов (длина l числа) равно 1 (h =2), то 1 log 2 2 =1 бит. Это и есть единица информации в принятой системе. Она соответствует одному элементарному событию, которое может произойти или не произойти. Помимо битов применяются единицы: ниты (натуральный логарифм) и диты (десятичный логарифм).
Аддитивная мера удобна тем, что она обеспечивает возможность сложения информации, поступающей от многих источников, и пропорциональность количества информации длине числа l, то есть количеству числовых гнезд. Введенное количество информации эквивалентно количеству двоичных знаков 0 и 1 при кодировании сообщения по двоичной системе счисления. При наличии нескольких источников информации общее количество информации суммируется: I(Q1, Q2…Qn) = I(Q1) + I(Q2)+…+I(Qn).