Двуальтернативная задача.

Пусть .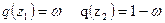

Будем считать, что при правильном выборе решения 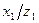, 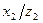потери статистика отсутствуют (или равны 0).

Тогда ошибка первого рода 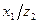дает потери 1, а ошибка второго рода 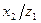дает потери .

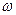Данная задача описывается матрицей потерь:

z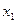

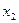
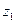
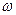
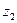
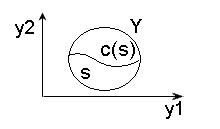
Рассмотрим решающую функцию x=d(y), которая делит пространство Y — множество исходов эксперимента на 2 подмножества: S и C(S): 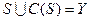, где C(S) — дополнение S до Y.

Если 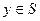, то принимается решение ;

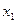Если 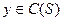, то принимается решение .

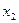Так как множества S и C(S) должна быть компактными, необходимо найти границу этого подмножества. Обозначим через 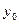— элементы, принадлежащие этой границе. Очевидно, что если множество исходов эксперимента можно описать в виде прямой, то 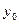— это точка на этой прямой. На плоскости 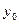— это линия.

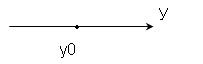
Для нахождения уравнения определяем границу 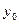. Рассмотрим выражение для средних потерь. Учитывая данные, приведенные в таблице, потери будут определяться:

.

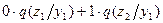В общем случае потери .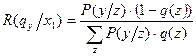

Граница 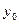соответствует одинаковым потерям при решени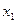и и 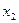. Для рассматриваемой задачи уравнение, определяющее границу, определяется как:

.

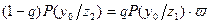Отношение правдоподобия в этом случае:

.

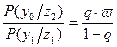Из этого условия следует, что каждому значению q будет соответствовать своя граница 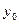и соответственно области S и C(S). Аналогично вероятности ошибочных решени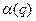й и 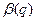будут определяться априорной вероятностью q. 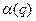— вероятность ошибки первого рода; 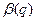- вероятность ошибки второго рода. Эти вероятности показывают вероятность того, что при 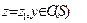, а при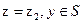

Тогда более развернуто:

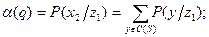
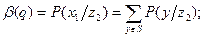
Для определения характера зависимости вероятностей ошибочных решений от q, сначала оцениваются крайние значения q=0 и q=1. Если 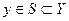, то принимается решение 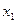, которое предполагает, что потери 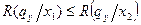. Выражая эти потери, можно получить, что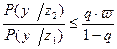

Предположим, что q=0. Это предполагает, что отношение .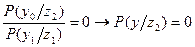

Это может быть только в том случае, если: 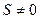, C(S)=Y. Если посчитать значения коэффициентов 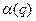=1, 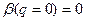С(S)=Y.

В другом крайнем состоянии q=1, получаем:

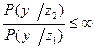. Это может быть, когда .

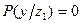Это условие определяет, что множество исходов эксперимента Y=S, C(S)= 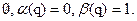Таким образом, вероятности ошибок при изменении .

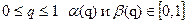Определим средние потери при любом значении 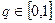как байесовские риски:

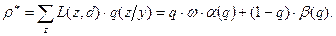
Если рассмотреть график зависимости 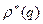, то он будет иметь вид вогнутой кривой:

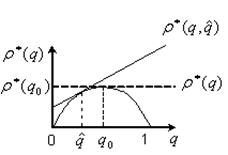
На практике встречаются случаи, когда значение q неизвестно, а известна его оценка 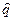. Возникает вопрос: «Как поступить?».

При приближенной оценке получим :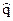

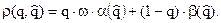
Если 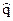— грубая оценка, то потери 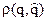могут стать больше максимальных потерь при 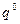, то есть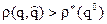

При значимом отличие q от 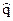, потери 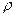невыгодны и в этом случае удобнее исходить из наиболее неблагоприятного 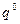. Ориентированные на потери 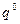можно рассматривать как минимаксные потери, стратегию 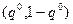как минимаксную стратегию. Применение байесовских принципов оправдано, когда q хорошая оценка 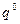, а при плохих оценках используется минимаксный принцип выбора стратегий.

Анализ целесообразности проведения

Экспериментов.

Пусть в результате проведения единичного эксперимента может появиться k исходов: 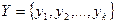. Предположим, что имеются вероятности 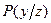. Множество состояний природы: 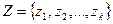. Обозначим 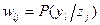— вероятность появления исхода эксперимента 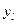при состоянии природы .

.

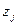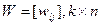Ясно, что для каждого j: .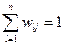

Считаем, что матрица W известна статистику. Кроме этого известна матрица выигрышей 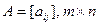, которая получена статистиком, используя стратегию 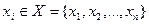в состоянии природы .

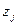Статистику известна стоимость проведения единичного эксперимента – с.

Анализируя эту информацию, статистик должен дать ответы на два вопроса:

1. целесообразно или нет проведение эксперимента.

2. какую из решающих функций необходимо при этом использовать, если эксперимент будет проводиться.

Рассмотрим обоснования для оценки ответа на первый вопрос.

Пусть в результате эксперимента произошел некоторый исход 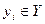. Апостериорные вероятности состояния природы 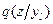обозначим в виде 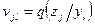. Эти вероятности определяют некоторую матрицу 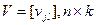, которую можно определить через апостериорные вероятности 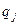по формуле Байеса: .

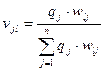С помощью апостериорных вероятностей для каждой из чистых стратегий статистика 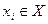можно определить условно средний выигрыш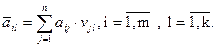

Оптимальную стратегию .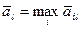

Величины 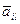являются случайными величинами, вероятность их появления совпадает с вероятностью исхода эксперимента.

Обозначим через 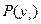вероятность l-ого исхода эксперимента. Она будет определяться вероятностью исхода при всех состояниях природы:

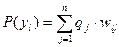
Тогда дополнительный выигрыш, который можно получить при проведении единичного эксперимента определяется следующим образом:

.

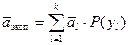Если 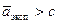, то эксперимент проводить стоит, если же наоборот, то не стоит.