Байесовской стратегии.
Пусть имеется игра с двумя состояниями природы L(V 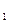 , a) и L(V
, a) и L(V 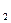 , a)
, a)
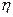 (a) — смешанная стратегия статистика.
(a) — смешанная стратегия статистика.
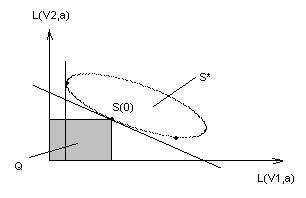
Построим вспомогательное множество, состоящее из всех точек, лежащих левее и ниже S 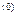 .
.
Считают, что множества S* и Q выпуклые и не пересекаются. Следовательно, можно провести прямую, разделяющую два этих множества. Эта прямая должна проходить через точку S 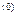 . Эта прямая является опорной.
. Эта прямая является опорной.
Эта прямая:
1. Вертикальная;
2. Горизонтальная;
3. Имеет отрицательный наклон
Уравнение y = -kx + c, k>0
ax + by = c’*k + 1>0
a = k/(k+1); b = 1/(k+1); c’ = c/(k+1); a, b, c >0; a + b = 1
Величины a и b можно толковать как вероятности состояний природы
a = 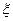 (V
(V 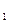 ) = W; b =
) = W; b = 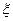 (V
(V 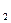 ) = 1-W; (1-W)*y = c’.
) = 1-W; (1-W)*y = c’.
Т. о. величина c’ определяет средние байесовские потери статистика L(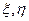 ) при априорных вероятностях W и (1-W) состояний природы. Нетрудно убедиться в том, что эти значения c’ являются минимальными для всех значений L(
) при априорных вероятностях W и (1-W) состояний природы. Нетрудно убедиться в том, что эти значения c’ являются минимальными для всех значений L(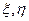 ), т. к. при c’’ > c’(справа от прямой) эта прямая не будет иметь общих точек с нижней левой границей и будет соответствовать недопустимым стратегиям статистика. Если c’’ < c’, то тоже не будет общих точек с S* (слева от прямой).
), т. к. при c’’ > c’(справа от прямой) эта прямая не будет иметь общих точек с нижней левой границей и будет соответствовать недопустимым стратегиям статистика. Если c’’ < c’, то тоже не будет общих точек с S* (слева от прямой).
Т. о. можно утверждать, что каждая допустимая стратегия статистика является байесовской при некоторых вероятностях состояния природы.
Можно показать обратную задачу: пусть известны W и (1-W) — вероятности состояния природы, V 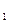 и V
и V 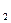 . Требуется определить точку S
. Требуется определить точку S 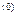
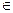 S*, соответствующую этим значениям вероятности. Тогда априорные вероятности W и (1-W) определят некоторую прямую W*x + (1-W)*y = c/
S*, соответствующую этим значениям вероятности. Тогда априорные вероятности W и (1-W) определят некоторую прямую W*x + (1-W)*y = c/
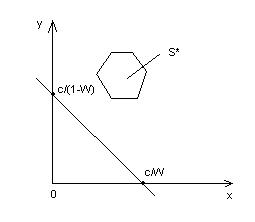 x/(1-W) + y/W = c’
x/(1-W) + y/W = c’
c’ = c/W(1-W), W 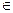 (0,1)
(0,1)
Если менять C’, то прямая будет перемещаться параллельно самой себе.
Далее рассмотрим выпуклую линейную оболочку дискретного множества чистых стратегий статистика S*.
Нижняя левая граница определяется двумя линиями. Меняя C’ можно добиться того, чтобы эта прямая касалась множества S*.
S* — многоугольник с вершинами, соответствующими чистым стратегиям статистика. В этом случая прямая должна проходить хотя бы через одну из его вершин. Следовательно, для любых чисел W и (1-W), являющихся априорными вероятностями состояния природы, всегда существует хотя бы одна байесовская стратегия статистика, которая является чистой. Это обстоятельство при поиске байесовских решений позволяет ограничиться анализом допустимых чистых стратегий статистка, а не рассматривать бесконечное число его смешанных стратегий.
Статистические игры с проведением единичного
Эксперимента.
Общие сведения.
Как отмечалось ранее, в статистических играх статистик имеет возможность проводить действия, углубляющие его сведения о состоянии природы (путём экспериментов).
Если нет ограничений во времени и средствах для проведения эксперимента, то статистик может получить полезную информацию о состоянии природы, однако суммарные затраты средств и времени, связанные с проведением эксперимента, могут превосходить дополнительный выигрыш, который может дать использование результатов этого эксперимента. В этой же ситуации возможность проведения эксперимента значительно расширяет класс стратегий статистика.
Проблемы:
1. Надо или нет проводить эксперимент;
2. Если надо, то сколько опытов произвести, чтобы считать эксперимент законченным;
3. Какие действия должен предпринимать статистик при тех или иных исходах эксперимента.
Сначала будем считать, что первый вопрос уже решён положительно.
При проведении эксперимента получаются различные его исходы. Например, единичный эксперимент заключается в n-кратном подбрасывании монеты: ГГРГГГРР… Г, (Г — герб, Р — решка). Всего возможных исходов 2 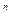 . Эти последовательности образуют пространство выборок (исходов эксперимента).
. Эти последовательности образуют пространство выборок (исходов эксперимента).
Пространство выборок.
Y = {y 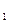 , y
, y 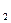 , …, y
, …, y 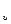 } — множество исходов эксперимента, y
} — множество исходов эксперимента, y 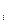 — i-ый исход эксперимента. Каждый из y
— i-ый исход эксперимента. Каждый из y 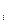 связан с соответствующим элементом состояния природы.
связан с соответствующим элементом состояния природы.
Z = {z 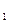 , z
, z 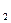 ,…, z
,…, z 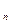 } — множество состояний природы. В общем случае статистическая связь:
} — множество состояний природы. В общем случае статистическая связь:
P(y/z) — условная вероятность исхода y при данном состоянии природы z.
P(y/z) 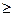 0;
0; 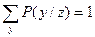 ,
, 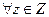 .
.
Совокупность из трёх элементов пространства Z, Y с заданными на Y условными вероятностями называют пространством выборок.
V = {x, y, P(y/z)}.
В конечномерном случае, когда m и 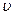 дискретно и конечно, то пространство выборок удобно рассматривать в виде таблицы, в которой строками являются состояния природы, столбцами — исходы эксперимента, а элементами — условные вероятности p
дискретно и конечно, то пространство выборок удобно рассматривать в виде таблицы, в которой строками являются состояния природы, столбцами — исходы эксперимента, а элементами — условные вероятности p 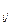 , которые определяют вероятности исхода y
, которые определяют вероятности исхода y  при состоянии природы z
при состоянии природы z 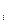 .
.
Пример: «задача о тест-контроле»
Состояния природы: z 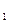 < ПДК
< ПДК
z 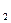 > ПДК
> ПДК
Три исхода: y 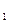 – вредных примесей не обнаружено;
– вредных примесей не обнаружено;
у 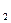 – вредных примесей обнаружено меньше ПДК;
– вредных примесей обнаружено меньше ПДК;
у 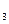 – вредных примесей обнаружено больше ПДК.
– вредных примесей обнаружено больше ПДК.
| z/y | P(y/z) | ||
| y1 | y2 | y3 | |
| z1 | 0,25 | 0,6 | 0,15 |
| z2 | 0,05 | 0,15 | 0,8 |
Очевидно, что при каждом исходе эксперимента, можно принимать какую-либо из гипотез.
y  X = {x
X = {x 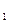 , x
, x 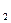 ,…, x
,…, x 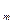 }
}
d(y) — решающая функция.
В играх без экспериментальных статистик решения принимают, исходя из априорных вероятностей состояния природы; статистик принимает решение, исходя из исхода эксперимента.
Чтобы формализовать задачу выбора своих решений, статистик должен заранее проанализировать все возможные исходы эксперимента и установить правило 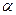 , позволяющее принимать решение x
, позволяющее принимать решение x 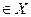 при каждом y
при каждом y 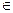 Y; d:
Y; d: 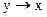 называют решающей функцией.
называют решающей функцией.
Пусть в задаче имеется возможность обрабатывать продукцию по технологиям x 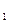 , x
, x 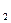 , x
, x 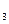 . Этот выбор должен осуществиться при исходах y
. Этот выбор должен осуществиться при исходах y 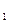 , y
, y 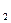 , y
, y 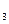 .
.
Решающая функция d(y 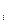 ) = x
) = x  . Эту функцию можно описать в виде пар (i, j).
. Эту функцию можно описать в виде пар (i, j).
Варианты построения решений:
1. (1, 1), (2, 1), (3, 2);
2. (1, 1), (2, 2), (3, 2) и т. д.
Для анализа нужно рассматривать пространство D, образованное всеми возможными решающими функциями. Каждая решающая функция разбивает множество Y исходов эксперимента на непересекающиеся подмножества S 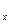 = {y: d(y) = x}
= {y: d(y) = x} 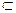 Y. Это непересекающееся множество можно определить для каждого x
Y. Это непересекающееся множество можно определить для каждого x 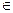 X. Для нашего эксперимента для первого случая S
X. Для нашего эксперимента для первого случая S  = {y
= {y 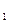 , y
, y 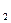 };
};
S 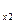 = {y
= {y 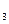 }; S
}; S 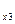 = {
= { 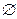 }. Аналогично можно сделать для каждой решающей функции.
}. Аналогично можно сделать для каждой решающей функции.
X = {x 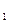 , x
, x 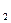 } — двухальтернативная задача. Решающая функция d(y) принимает два значения:
} — двухальтернативная задача. Решающая функция d(y) принимает два значения:
d(y) = 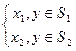 ; y = S
; y = S 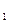
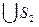 ; S
; S 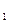
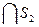 =
= 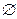
y в этом случае — критическая область.
Понятие «решающая функция» позволяет принимать (выбирать) такую из них, которая даёт наиболее выгодное решение. Возникает вопрос: как определить качество решающей функции? Качество решающей функции удобно оценивать с помощью функции риска.
Функции риска.
Пусть задана решающая функция:
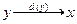
Очевидно тогда, каждому решению 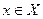 состояния природы z будут соответствовать потери статистика L(z,x).
состояния природы z будут соответствовать потери статистика L(z,x).
L(z,x)=L(z,d(y))= 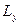 (z,d).
(z,d).
Они показывают потери статистика при состоянии z.
Исход у при данном состоянии природы z случаен и характеризуется вероятностью 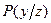 .
.
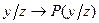 .
.
Очевидно, что с этой же вероятностью будут получаться потери 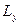 (z,d).
(z,d).
При определении качества d(y) нужно учитывать все у, появившиеся при данном z. Необходимо учитывать все возможные исходы эксперимента и вести речь о средних потерях.
Эти средние потери называют функцией риска.
Для оценки риска вводят следующую функцию:
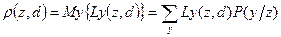 .
.
Каждой решающей функции и каждому состоянию природы будут соответствовать свои значения функции потерь 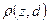 на множестве
на множестве  , где Z — множество состояний природы, а D — множество решающих функций.
, где Z — множество состояний природы, а D — множество решающих функций.
В играх с экспериментом статистик имеет возможность использовать не только чистые, но и смешанные стратегии.
Для формирования смешанной стратегии статистик должен использовать механизм случайного выбора решающих функций из 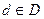 . Для этого нужно задать
. Для этого нужно задать 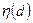 — распределение вероятности решающей функции d при смешанной стратегии статистика в игре с единичным экспериментом.
— распределение вероятности решающей функции d при смешанной стратегии статистика в игре с единичным экспериментом.
Если это распределение задано, то
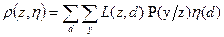 .
.
Очевидно, что либо чистая стратегия, либо смешанная будут наилучшими, если они минимизируют средние потери.

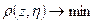
Пример: «Задача о тест-контроле продукции».
Пусть 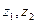 — состояния природы.
— состояния природы.
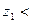 ПДК;
ПДК;
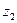 >ПДК.
>ПДК.
Исходы эксперимента:
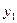 — примесей нет,
— примесей нет, 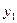 =0.
=0.
 — примесей<ПДК;
— примесей<ПДК;
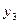 — примесей>ПДК;
— примесей>ПДК;
х — наше решение.
Тогда эту игру с природой можно описать следующей таблицей:
| z | 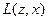
| 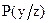
| ||||
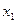
| 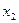
| 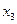
| 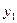
| 
| 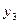
| |
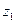
| 0,25 | 0,6 | 0,15 | |||
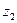
| 0,05 | 0,15 | 0,8 |
Так как d(y) принимает значения 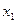 ,
, 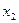 ,
, 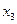 , то d(y)={
, то d(y)={ 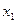 ,
, 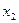 ,
, 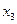 }
}
Найдем для этой функции потери:
Для состояния 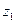 :
:
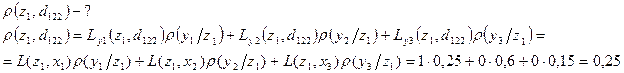
Для состояния 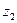
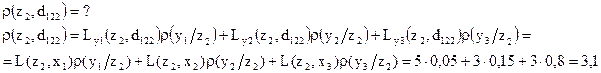
Такие же потери можно посчитать для любой другой (допустимой) решающей функции. Посчитанные таким образом значения можно представить графически на плоскости.