Основы работоспособности технических систем.
Практикум
Пенза 2011
УДК 629.33. 083.4 (075.8)
ББК 39.33-08я73
Б 43
Рецензенты: директор некоммерческого партнерства автотранспортного союза Пензенской области, член правления Российского автотранспортного союза В.И. Тюкалов, кандидат технических наук, доцент кафедры АСУТ ПГУАС А.С. Ширшиков
| Б43 | Белоковыльский А.М.Основы работоспособности технических систем: Учеб. пособие / А.М. Белоковыльский, В.В. Лянденбурский, А.С. Иванов. – Пенза: ПГУАС, 2011. – 144 с.: Табл.27. Ил.36. Библиогр.: 25 назв. |
В учебном пособии приведены теоретические сведения и изложена методика проведения лабораторных работ и практических занятий по дисциплине «Основы работоспособности технических систем».
Учебное пособие подготовлено на кафедре «Автомобили и автомобильное хозяйство» и предназначено для студентов дневной очной формы обучения специальности 190603 “Сервис транспортных и технологических машин и оборудования (автомобильный транспорт)” и направления подготовки бакалавров 190600 “Эксплуатация транспортно-технологических машин и комплексов ”.
ã Пензенский государственный
университет архитектуры и строительства, 2011
ã А.М. Белоковыльский, В.В. Лянденбурский, А.С.Иванов, 2011
ПРЕДИСЛОВИЕ
Учебное пособие состоит из двух частей: Часть 1 - «Лабораторные работы», Часть 2 - «Практические занятия».
В первой части представлены краткие теоретические сведения, приведен порядок выполнения лабораторных работ: “Определение распределения ресурса объекта”, “Расчет надежности систем по критерию работоспособности”, “Обработка экспериментальных данных по результатам измерений”, “Испытания конструкционных материалов на изнашивание”, “Исследование влияния эксплуатационных факторов на интенсивность изнашивания”, “Диагностирование электрооборудования двигателя легкового автомобиля с использованием мотор-тестера Ц4328”, “Порядок проведения ТО автомобилей”, “Прогнозирование технического состояния автомобилей”.
Во второй части представлены краткие теоретические сведения, приведена методика проведения практических занятий: “Контроль показателей надежности по данным эксплуатации”, “Анализ экспериментальных данных”, “Исследование влияния системы технического обслуживания и ремонта на надежность автомобиля”, “Обоснование рациональной периодичности технического обслуживания элемента автомобиля с помощью имитационного моделирования”, “Оптимизация количества постов СТО”, “Оптимизация нормативов ТО и ремонта", "Определение периодичности диагностирования”, “Оценка экономической эффективности от внедрения средств технического диагностирования на СТО.
Практикум разработан на кафедре “ААХ” и предназначен для студентов дневной очной формы обучения специальностей 190603 “Сервис транспортных и технологических машин и оборудования (автомобильный транспорт)” и 190702 “Организация и безопасность движения”, а также направлений подготовки 190600 “Эксплуатация транспортно-технологических машин и комплексов ” и 190700 “Технология транспортных процессов ”.
Практикум подготовлен к изданию Белоковыльским А.М. на основе указанных литературных источников, а также личных исследованиях автора. Кроме того, при написании практикума также были использованы отдельные, ранее опубликованные материалы В.В. Лянденбурского и А.С. Иванова.
Автор приносит свои извинения за возможные допущенные ошибки и просит направлять свои отзывы и пожелания.
Автор благодарит сотрудников редакционно-издательского отдела ПГУАС и полиграфического центра за помощь в издании данной книги. Отдельная благодарность выражается Хлебушкину В.М. за помощь в редактировании книги.
ВВЕДЕНИЕ
Техническую эксплуатацию автомобилей (ТЭА) можно представить и как область практической деятельности, и как науку, которая определяет пути и методы наиболее эффективного управления техническим состоянием автомобиля и автомобильного парка с целью обеспечения регулярности, безопасности и экономичности перевозок.
Настоящий практикум предназначен для закрепления теоретических знаний по дисциплине «Основы работоспособности технических систем», полученных обучающимися по вопросам ТЭА, а также их прикладного применения при решении практических задач. Практикум издается впервые и обеспечивает преемственность знаний, полученных обучающимися при изучении предшествующих и последующих дисциплин, одновременно являясь связующим звеном между теоретическими положениями и практическими умениями и навыками, формирующимися в результате освоения учебного курса.
Инженер по специальности “Сервис транспортных и технологических машин и оборудования (автомобильный транспорт)”, бакалавр по направлению подготовки “Эксплуатация транспортно-технологических машин и комплексов” должен не только знать существующие технологии технической эксплуатации автомобилей, но и уметь разрабатывать их самостоятельно, а также принимать обоснованные и верные решения при осуществлении своей профессиональной деятельности. Творческое решение проблем автомобильного транспорта возможно только путем овладения теоретическими знаниями и их умелого применения на практике.
Кроме того, практикум может быть использован для проведения лабораторных работ по дисциплинам: “Техническая эксплуатация автомобилей” для специальности 190601 “Автомобили и автомобильное хозяйство”, “Основы технической эксплуатации подвижного состава” для специальности 190702 “Организация и безопасность движения”, а также “Техника транспорта, обслуживание и ремонт” по направлению подготовки 190700 “Технология транспортных процессов”.
Практикум составлен в соответствии с ГОС 2-го поколения по специальности “Сервис транспортных и технологических машин и оборудования (автомобильный транспорт)” с учетом ГОС 3-го поколения по направлению подготовки “Эксплуатация транспортно-технологических машин и комплексов” на основе указанных литературных источников, а также материалов ислледований и публикаций авторского коллектива.
Имеющиеся в конце каждой лабораторной работы и практического занятия вопросы для самостоятельной работы значительно облегчают самостоятельное изучение и закрепление материала обучающимися.
ЧАСТЬ 1
ЛАБОРАТОРНЫЕ РАБОТЫ
Лабораторная работа №1
ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК РАСПРЕДЕЛЕНИЯ РЕСУРСА ОБЪЕКТА
Цель работы: изучить методику обработки полной информации о надежности машины.
Задачи работы:
1. Изучить методику определения точечных характеристик распределения показателя надежности машины.
2. Ознакомиться с методами выбора теоретического закона распределения ресурса машины.
3. Изучить методику расчета интервальных характеристик распределения ресурса машины.
Теоретическая часть [3, 4, 5, 10, 14]
Технический объект (объект) - это предмет, подлежащий расчету, анализу, испытанию и исследованию в процессе его проектирования, изготовления, применения, технического обслуживания, ремонтов, хранения и транспортирования в целях обеспечения эффективности его функционального назначения.
Надежность – это свойство объекта выполнять и сохранять во времени заданные ему функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортирования.
Надежность является комплексным свойством, включающим в себя четыре единичных свойства: безотказность, долговечность, ремонтопригодность, сохраняемость.
Безотказность – свойство объекта сохранять работоспособность непрерывно в течение некоторого времени или некоторой наработки. Свойство безотказности проявляется в зависимости от назначения объекта как в ре жиме его работы, так и в режиме ожидания работы.
Долговечность – свойство объекта сохранять работоспособность до перекода в предельное состояние с возможными перерывами для технического обслуживания и ремонтов.
В отличие от свойства безотказности долговечность характеризует продолжительность работы объекта по суммарной наработке, прерываемой периодами для восстановления его работоспособности в плановых и неплановых ремонтах и техническом обслуживании.
Ремонтопригодность – свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению отказов и повреждений, к восстановлению работоспособности и исправности путем проведения технического обслуживания и ремонта.
Сохраняемость – свойство объекта непрерывно сохранять исправное и (или) работоспособное состояние в течение и (или) после режима ожидания, хранения и (или) транспортирования
Каждое из перечисленных свойств характеризуется определенными показателями, в том числе и долговечность, оцениваемая средним ресурсов, гамма процентным ресурсом, назначенным ресурсом.
Под назначенным ресурсом до списания понимается наработка объекта до наступления его предельного состояния. Поскольку ресурс объекта является случайной величиной, так как зависит от значительного количества факторов, он оценивается точечными статистическими характеристиками: средним значением, среднеквадратическим отклонением (стандартом), дисперсией рассеивания, коэффициентом вариации.
Перечисленные характеристики, как правило, оценивают ту выборку объектов, для которой они были рассчитаны. Выборка объектов значительно меньше генеральной совокупности объектов и ее характеристика не может быть перенесена на все объекты.
Для того, чтобы результаты испытаний можно было бы применить для оценки генеральной совокупности (всех объектов в рассматриваемой зоне) используются интервальные характеристики: нижняя и верхняя доверительные границы рассеивания одиночного и среднего значения показателя надежности, доверительная вероятность, относительная ошибка переноса.
Доверительная вероятность - это величина, характеризующая степень доверия к границам значений показателя надежности (одиночного и среднего), как правило, она принимается равной 0.8, 0.9, 0.95.
Границы, в которых может колебаться одиночное или среднее значение показателя надежности при заданной a, называются нижней и верхней доверительными границами.
Определение перечисленных характеристик распределения целесообразно выполнять с помощью математического пакета MathCad, позволяющего использовать не только функции составленные пользователем, но и применять встроенные статистические функции (приложение 1) [14].
В целом последовательность расчета сводится к следующим этапам [3, 4, 5, 14]:
- создание файла с исходной информацией о ресурсах машин взятых под наблюдение,
- определение точечных характеристик,
- проверка информации на выпадающие точки, т.е. значения которые существенно отличаются от основного массива, проверка может быть выполнена по правилу "3s" или с помощью критерия Ирвина,
- для того, чтобы получить интервальные характеристики, определяется теоретический закон распределения (ТЗР) ресурса с помощью коэффициента вариации, визуально, сравнением полигона распределения и дифференциальных функций ТЗР, и с помощью критерия Пирсона c2,
- распределение ресурса представляется в виде графиков: гистограммы (ступенчатого графика), полигона (ломаной кривой соединяющий середины интервалов статистического ряда, соответствующие опытным вероятностям интервалов) и кривой накопленных опытных вероятностей интервалов,
- после выбора ТЗР рассчитываются интервальные характеристики распределения.
При выполнении расчетов используются некоторые специальные статистические термины:
Квантиль ta заданной доверительной вероятности a - это такая величина, при которой соблюдается равенство P(t<ta) = a, где P(t<ta) - вероятность того, что случайная величина t не превысит значения квантили t a. Квантилью называют значение случайной величины, соответствующее заданной вероятности.
Генеральная совокупность - множество, включающее все однородные объекты с исследуемыми качествами.
Случайная выборка - часть генеральной совокупности, выбранная наугад.
Репрезентативная выборка - выборка, в которой пропорции различных типов в среднем соответствуют пропорциям в генеральной совокупности
Частость (относительная частота) - это отношение количества событий, которые имели место к общему количеству.
Теоретический закон распределения случайной непрерывной величины характеризуется интегральной и дифференциальной функциями.

Рис. 1.1. Интегральная и дифференциальная функции ТЗР
Интегральная функция F(t) (функция распределения) показывает вероятность возникновения события (отказа) в интервале от 0 до заданного значения наработки t. (рис.1.1).
Дифференциальная функция f(t) (плотность распределения) характеризует вероятность возникновения в заданном интервале наработки.
Аналитические выражения интегральных и дифференциальных функций распределения некоторых теоретических законов, а также осноные параметры распределений приведены в приложении 2.
Порядок выполнения работы
Методика обработки статистической информации о ресурсе машины с помощью MathCad
1.Исходную информацию о ресурсе машины записываем в текстовый файл в виде колонки чисел, в том же каталоге, где находится протокол MathCad, используя простейший редактор Windows "Блокнот".
2.После этого вводим информацию в протокол MathCad с помощью функции READPRN и определяем количество информации с помощью функции length. Предварительно переменной MyFile присваиваем имя текстового файла с данными о ресурсах машин.




где Х - вектор наработок на отказ исследуемого элемента автомобиля, км пробега в порядке возрастания его элементов;
N – количество информации, длина вектора.
3. Строим вариационный ряд, расположив информацию о ресурсе машины в порядке возрастания с помощью функции sort и присваиваем каждому элементу вектора индекс j


4.Определяем точечные характеристики распределения ресурса
- определяем общее число интервалов n в статистическом ряду по формуле



где nd - количество дополнительных интервалов,
- рассчитываем величину интервала


- рассчитываем величину смещения распределения


- определяем среднее значение наработки


- рассчитываем среднеквадратическое отклонение,


- рассчитываем коэффициент вариации наработки на отказ


5. Проверяем информацию на выпадающие точки с помощью критерия Ирвина
- рассчитываем значение критерия Ирвина для минимального ресурса в вариационном ряду информации


- рассчитываем значение критерия Ирвина для максимального ресурса в вариационном ряду информации


- рассчитываем критическое значение критерия Ирвина для вероятности 0,99 по эмпирической формуле


Если расчетное значение критерия Ирвина для ресурса больше критического, то минимальное или максимальное его значение является выпадающей точкой и его следует удалить из исходной информации (из текстового файла с исходной информацией) и расчет повторить заново.
Очистку информации от выпадающих точек продолжаем до тех пор, пока не будет выполнено условие
l0<lКР и lN-1<lКР.
6. Выбраем теоретический закон распределения.
6.1. По коэффициенту вариации принимаем закон распределения ресурса машины: закон нормального распределения или закон распределения Вейбулла, так как коэффициент вариации находится в пределах 0,33 – 0,7.
6.2. Закон распределения можно выбрать визуально на основании сравнения полигона распределения и дифференциальных функций законов, принятых в п. 6.1.
Для этого строим графики, предварительно определив частоту попаданий в каждый интервал m, используя функцию MathCad hist, и присваиваем индекс интервалам i.


Создаем также вектор начальных Xn, конечных Xk и средних значений Xc для каждого интервала интервалов



Результаты расчетов представляем в виде векторов значений





Определяем накопленные опытные вероятности mSz, соответствующие конечным наработкам интервалов, предварительно присвоив им индекс z


Строим графики по опытным данным (рис.1.2):
- гистограмму (ступенчатый график) и полигон распределения (ломаная кривая) m/N по частости, опытной вероятности m/N
- кривую накопленных опытных вероятностей mS Рассчитываем значения теоретических функций для интервалов.
Дифференциальную функцию нормального закона распределения рассчитать по формуле


Рис. 1.2. Опытные кривые распределения ресурса машины
Перед расчетом дифференциальной функции закона Вейбулла определяем параметры этого закона:
- параметр формы закона Вейбулла b определяем поформулам, полученным путем аппроксимации табличных данных


- масштабный параметр a рассчитываем, предварительно определив коэффициент Kb по формуле



 .
.
Дифференциальную функцию закона распределения Вейбулла рассчитываем по формуле

Результаты расчета представляем в виде векторов, с использованием которых строим график (рис.1. 3)




Рис. 1.3. Полигон распределения и дифференциальные функции теоретических законов (ЗНР и ЗРВ)
6.3. Для более точного выбора закона распределения целесообразно использовать критерий Пирсона χ2




Допустимая вероятность совпадения опытных данных с расчетными по критерию χ2 равна 10%:.
Требуемый уровень значимости принимаем равным ε:=0,15.
Число степеней свободы определяем по выражению


Расчетные вероятности совпадения опытных данных с теоретическими
- для нормального закона распределения


- для закона распределения Вейбулла


Таким образом, закон распределения Вейбулла, имеющий большую вероятность, принимаем как закон распределения ресурса машины
7. Определяем интервальные характеристики распределения ресурса генеральной совокупности машин
При расчете интервальных оценок распределения задаться доверительной вероятностью, например 0,95
 .
.
Затем используем известные формулы и встроенные функции MathCad для определения квантилей закона распределения Стьюдента и Вейбулла. П ри количестве информации менее 100 вместо нормального закона распределения рекомендуется использовать закон распределения Стьюдента.
- доверительные границы одиночного значения показателя надежности для нормального закона распределения




где qt(α, N) – встроенная функция MathCad, позволяющая определить квартиль распределенияя при заданной доверительной вероятности α и количестве информации N.
- доверительные границы одиночного значения показателя надежности для закона распределения Вейбулла




Доверительные границы среднего значения ресурса определяем, не зависимо от теоретического распределения, по выражению




Верхняя доверительная одностороння граница среднего значения ресурса машины


Относительную предельную ошибку переноса определяем при односторонней доверительной вероятности a0=(1+a)/2. Относительная ошибка не должна превышать 10-20%.


Содержание отчета
1. Протокол MathCad расчета характеристик распределения: точечных и интервальных с результатами расчета и графиками.
2. Выводы по результатам работы.
Вопросы для самостоятельной работы
1.Что такое технический объект?
2. Что такое надежность?
3. Что такое безотказность, ремонтопригодность, долговечность, сохраняемость?
4.Что такое ресурс машины?
5.Что такое предельное состояние машины?
6.Перечислите точечные и интервальные характеристики распределения показателя надежности.
7. С какой целью определяются интервальные оценки распределения ресурса?
8. Что такое доверительная вероятность?
9. Что такое доверительные границы распределения показателя надежности?
10. Последовательность расчета характеристик распределения ресурса.
11. Что такое квантиль доверительной вероятности?
13. Что такое частость?
14.Что характеризуют дифференциальная и интегральная функции закона распределения?
15.Как рассчитать точечные характеристики ресурса?
16.Как проверить информацию на выпадающие точки?
17. Какими способами можно воспользоваться для выбора теоретического закона распределения?
18.Что такое статистический ряд и укрупненный статистический ряд?
19. Как определить число интервалов в укрупненном статистическом ряду?
20. Как построить гистограмму, полигон и кривую накопленных опытных вероятностей?
21.Как построить дифференциальные функции теоретических законов распределения:ЗНР и ЗРВ?
22.Сущность и назначения критерия Пирсона?
23. Как рассчитать доверительные границы для одиночного и среднего значения ресурса?
24. Как определить предельную ошибку переноса?
Лабораторная работа №2
РАСЧЕТ НАДЕЖНОСТИ СИСТЕМ ПО КРИТЕРИЮ РАБОТОСПОСОБНОСТИ
Цель работы: научиться рассчитывать надежность (безотказность) систем с различным соединением элементов.
Задачи работы:
1. Изучить теоретические основы расчета вероятности безотказной работы систем с различным соединением элементов.
2. Приобрести навыки формализации технических систем в структурные и функциональные схемы.
3. Провести расчеты вероятности безотказной работы систем с различным соединением элементов.
Теоретическая часть [ 3, 4, 5, 10 ]
Техническая система (ТС)– сложный объект, представляющий собой совокупность взаимосвязанных функционально и расположенных в определенном порядке объектов.
Элемент (технической системы) – объект, представляющий собой часть ТС в конкретном рассматриваемом исследовании.
Исправное состояние (исправность) – состояние объекта, при котором он удовлетворяет всем требованиям нормативно-технической документации (НТД).
Неисправное состояние (неисправность) – состояние объекта, при котором он не удовлетворяет хотя бы одному из требований НТД.
Работоспособное состояние (работоспособность) – состояние объекта, при котором значения всех параметров, характеризующих его способность выполнять заданные функции, соответствуют требованиям НТД.
Неработоспособное состояние (неработоспособность) – состояние объекта, при котором значение хотя бы одного параметра, характеризующего его способность выполнять заданные функции, не соответствуют требованиям НТД.
Предельное состояние – состояние объекта, при достижении которого его дальнейшее применение по назначению недопустимо или невозможно.
Повреждение – событие, заключающееся в нарушении исправности объекта при сохранении его работоспособности.
Отказ – событие, заключающееся в нарушении работоспособности объекта.
Автомобили в периоды их использования, хранения, транспортирования, ТО и ремонта в течение всего срока службы всегда находятся в одном из рассмотренных выше четырех состояниях. Особым видом неработоспособного состояния является предельное состояние. Переход из одного состояния в другое фиксируется событиями – повреждением или отказом.
Ремонтируемый объект – объект, для которого возможность проведения ремонтов и ТО предусмотрена в НТД.
Автомобили относятся к классу ремонтируемых объектов.
Неремонтируемый объект – объект, для которого возможность проведения ремонтов и ТО не предусмотрена в НТД.
К ним могут быть отнесены подшипники качения, шпонки, клиновые ремни, манжеты, уплотнения и т.д., нарушение работоспособности которых по критерию прочности или предельного износа соответствует их переходу в предельное состояние с последующей сдачей в утиль.
Показатель надежности – величина, характеризующая одно из свойств (единичный показатель) или несколько свойств надежности (комплексный показатель).
Наработка – это продолжительность или объем работы изделия. Для автомобиля естественно исчисление наработки в километрах пробега, тогда как для других технических средств могут быть удобнее иные единицы измерения (например, наработка радиоэлектронных систем измеряется в единицах времени, наработка станков – в единицах выпущенной продукции).
Безотказность изделий характеризуется следующими показателями: вероятностью безотказной работы, интенсивностью отказов, наработкой до отказа, наработкой на отказ.
Вероятность безотказной работы (ВБР) – вероятность того, что в пределах заданной наработки (срока службы) отказ в изделии не возникает. Символически это определение можно записать в виде формулы (1.1):
Р(t) = p(Q > tз), (1.1)
где Q - случайное время (наработка) возникновения отказа;
tз – заданное время (наработка).
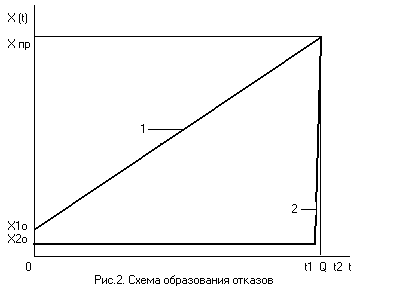
Графически интерпретировать это определение можно с помощью рис.1.4, где условно показан характер возникновения 1 - постепенного и 2 - внезапного отказов. На рис. 1.4 Х 1,0, Х 2,0 соответствуют начальным значениям каких-либо параметров изделия, а Х ПР – предельному значению параметра.
Кроме ВБР при оценке безотказности изделий используется и другая вероятность – вероятность отказа (ВО). Вероятность отказа - это вероятность события, противоположного работоспособности изделия.
Вероятностью отказа (ВО) называется вероятность того, что случайное время возникновения отказа Q (см. рис. 1.4) окажется меньше заданного времени t2, т.е.
F(t) = p(Q < t2). (1.1)
| Рис. 1.4. Схема формирования отказов |
Таким образом, ВБР и ВО являются вероятностями двух противоположных событий, следовательно вполне справедлива формула
(1.2):
Р (t) + F (t) = 1. (1.2)
Графическая интерпретация ВБР Р(t) и ВО F(t) показана на рис. 1.5.
| Рис. 1.5. График зависимости P(t) и F(t) |

ВБР можно рассчитать по статистической формуле (1.3):
 , (1.3)
, (1.3)
где No – число изделий до начала испытаний (наблюдений);
t2 – t1 – отрезок времени (наработки), в течение которого велись испытания (наблюдения);
n(t2 – t1) – число изделий, отказавших за время (t2 – t1).
По формуле (1.3) можно определить ВБР только за отрезок времени (t2 – t1) и невозможно определить Р(t) за другой период времени.
В вероятностной постановке, ВБР и ВО, с учетом того, что изделия имеют наработку до отказа Т, а t является заданной наработкой, т.е. вероятность Вер(T ³ t), будут между собой связаны следующим соотношением.

Прогнозировать ВБР можно на основе теоретических зависимостей, когда известны законы распределения времени возникновения отказов.
Интенсивность отказов (lt) – отношение числа изделий n(t), отказавших в единицу времени, к среднему числу изделий N СР, исправно работающих в данный отрезок времени D t, при условии, что отказавшие изделия не восстанавливаются и не заменяются новыми т.е.

где n(t) – число отказавших изделий за время D t (в интервале t…t+Dt);
D t – интервал времени;
 , (1.5)
, (1.5)
где N(t) – количество изделий до начала испытаний (наблюдений);
N(t+Dt) = N(t) – n(t) – количество работоспособных изделий, оставшихся после испытаний.
| Рис. 1.6. График интенсивности отказов по периодам эксплуатации |
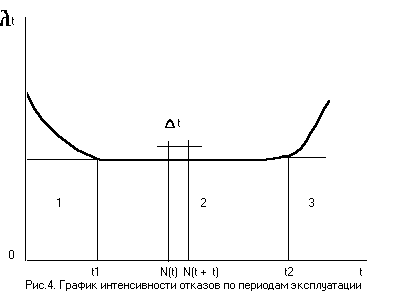
Для многих элементов `l(t) имеет закономерность, приведенную на рис. 1.6, где можно выделить три характерные периода:
(0... t1) - (1-й период) – участок приработки. На этом участке l(t) определяется функцией;
(t1…t2) – (2-й период) – участок нормальной эксплуатации.
Для многих элементов в этот период имеют место только внезапные отказы. Следовательно, на этом участке интенсивность отказов может быть найдена по следующей формуле:
 (1.6)
(1.6)
Интегрируя (1.6), легко получить:
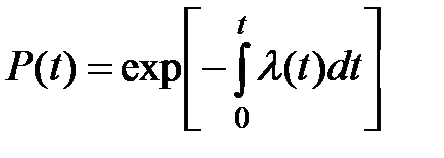 . (1.7)
. (1.7)
Это выражение является одним из основных уравнений теории надежности. В частном случае постоянства интенсивности отказов v(t)=λ= const (1.5) переходит в известное в теории вероятностей экспоненциальное распределение:
P (t)=e–v t; F (t)=1–e–v t; f (t)=ve–v t (1.8)
после t 2 – (3-й период), в течение которого к внезапным отказам добавляются еще постепенные отказы, связанные с повышенным износом и старением. В этом периоде l(t) непостоянна, определяется функцией.
Понятие интенсивности отказов используется в основном невосстанавливаемых изделий.
Для восстанавливаемых изделий используется понятие параметра потока отказов w (t), которым называется отношение изделий, отказавших в единицу времени, к числу испытываемых изделий при условии, что все отказавшие изделия восстанавливаются и продолжают работать. На основе этого имеем:
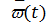 =
=  = f(t), (1.9)
= f(t), (1.9)
то есть `w(t) численно равен ¦(t),
где n å(t) – число всех отказов, полученных за время Dt;
N o – число изделий, участвующих в испытаниях.
Поток отказов при v(t)=const называется простейшим. Он реализуется в течение периода нормальной эксплуатации от окончания приработки до начала периода повышенного старения и износа (см. рис. 1.6). Простейший параметр потока отказов, который характеризуется тремя основными свойствами – стационарностью, ординарностью и без последействием:
1- если w (t) = const, то поток считается стационарным;
2– если вероятность возникновения одновременно двух отказов близка к нулю, то поток называется ординарным;
3 – если отказы независимы, то поток считается без последействия.
Для простейшего потока отказов применим закон Пуассона:
 , (1.10)
, (1.10)
где pm - вероятность возникновения m отказов за время t.
Наработка до отказа (среднее время безотказной работы) Тср, `Т (для не восстанавливаемых изделий) – среднее значение наработки изделия между отказами при условии восстановления каждого отказавшего элемента.
В вероятностной постановке:
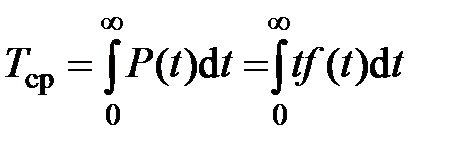 (1.11)
(1.11)
где t – значения наработки до отказа;
P (t) – вероятность безотказной работы (см. (1.8));
f (t) – плотность распределения наработки до отказа, характеризующая распределение отказов во времени: