Цель работы – изучить методику проведения и обработки результатов полнофакторного эксперимента при исследовании износостойкости деталей.
Задачи работы:
1. Изучить методику полнофакторного эксперимента и подготовить исходные данные для его проведения.
2. Выполнить полнофакторный эксперимент с помощью виртуальной машины ВМИ-1М.
3. Произвести обработку результатов эксперимента с помощью системы MathCad.
4. Проанализировать результаты эксперимента и сделать выводы.
Теоретическая часть [2, 9, 10]
На интенсивность изнашивания деталей влияют не только вид трения и характеристики детали, но и эксплуатационные факторы, к которым относятся температура смазочного материала, концентрация абразивных частиц в масле, а также давление в зоне контакта трущихся деталей.
Повышение температуры поверхности трения и масла в некоторых пределах вполне допустимо, при этом наблюдается установившееся коррозионно-механическое изнашивание. При критическом значении температур, которые определяются давлением на поверхности трения и скоростью относительного перемещения, составом среды и природой контактирующих материалов, происходят резкие изменения вторичных структур, интенсивность микроразрушений увеличивается, как правило, в несколько раз. По результатам металлографического анализа можно определить критическое значение нагрузки (давления и скорости относительного перемещения поверхностей трения), при которых резко увеличится интенсивность изнашивания для заданных трущихся материалов и масла.
Зависимость интенсивности изнашивания от температуры является весьма сложной, однако, с достаточной для практических целей точностью ее можно принять линейной:

где Da и Dt— изменение соответственно интенсивности изнашивания и температуры;
aо - интенсивность изнашивания при Dt = 0;
b - коэффициент.

Рис. 1.27. Влияние температуры t масла в картере на изменение интенсивности изнашивания a цилиндров двигателя на расстоянии 8мм от верхней плоскости блока цилиндров (1) и 90мм (2). Для коренных шеек коленчатого вала кривая аналогична (1)
Зависимость интенсивности изнашивания от давления и скорости будут аналогичными:

где aо - интенсивность изнашивания соответственно при Dр = 0 и Dv = 0;
a1 = bq/yF,
- bp - при р о = 0 и D v = 0, a = a1 (1 – exp);
- bv - при v o = 0 и D p = 0, a = a1 (1 – exp),
где a1 - интенсивность изнашивания соответственно при р Þ ¥ или v = Þ ¥.
На основе полученных зависимостей можно установить закономерность изменения долговечности деталей от нагрузки, скорости и температуры на поверхности трения. На основе принятого допущения Da = bDt.
Зависимость долговечности l деталей от Dp и D v при p o = 0, D v = 0

где l 1 - долговечность при p Þ ¥, S п — предельный износ. Аналогично при v o = 0, D p o = 0 получим:

где l l — долговечность при v = Þ ¥.
Зависимость долговечности детали от температуры на поверхности трения

где l о - пробег до предельного состояния при D р =0, D v o = 0; c = b /ao.
Таким образом, полученные аналитические зависимости позволяют прогнозировать изменение температуры, интенсивности изнашивания и долговечности детали в зависимости от изменения нагрузочного и скоростного режимов работы сопряжения. При этом изменять интенсивность изнашивания могут не только перечисленные факторы, но и их взаимодействия. Использование традиционного однофакторного эксперимента для выявления зависимости интенсивности изнашивания от нескольких параметров не позволит эффективно решить поставленную задачу.
В данном случае для нахождения наиболее адекватной модели для описания интенсивности изнашивания целесообразно применять методику активного эксперимента, в основу которого положено планирование проведения опытов [2, 9, 10].
Таким образом, задача, связанная с получением наилучшего представления о влиянии выбранных факторов на интенсивность изнашивания, сводится к выбору оптимального плана испытаний. Наиболее простым, но эффективным является ортогональный факторный план, при котором каждый фактор изменяется относительно начала координат на двух уровнях. Этого легко можно достигнуть, если принять верхний уровень фактора x (+1), а нижний (-1).
Чтобы составить ортогональный план, необходимо рассмотреть всевозможные неповторяющиеся комбинации из двух уровней факторов. Число N различных экспериментов, определяемое числом всех неповторяющихся комбинаций, которые можно составить из k рассматриваемых независимых переменных, имеющих по два уровня, будет N = 2 k. Если осуществляют все 2 k возможных и неповторяющихся комбинаций, то получают полный факторный эксперимент (ПФЭ).
Выбор области экспериментирования связан с детальным анализом априорной информации, на основании которого принимаются решения относительно основного уровня (центра эксперимента), интервалов варьирования. Вопросы формализации анализа априорных данных для принятия решений на этом неформализованном этапе перед планированием эксперимента рассмотрены в работе [9, 10].
Основной (нулевой) уровень рассматривается как исходная точка эксперимента, задаваемая комбинацией нулевых уровней факторов.
План 2 k эксперимента задает способ симметричного расположения экспериментальных точек (опытов) относительно нулевого уровня. Симметричное расположение точек достигается выбором интервалов варьирования.
Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, и вычитание – нижний уровни фактора.
Для упрощения записи условий каждого опыта и обработки выборочных данных эксперимента масштабы по осям факторов выбираются так, чтобы верхний уровень соответствовал +1, нижний – 1, а основной – нулю. Это легко достигается с помощью преобразования  ,
,
где хj – кодированное значение j -гo фактора; Xj – натуральное значение фактора; Xj0 – натуральное значение основного уровня фактора; D Xj – интервал варьирования j -гo фактора.
Пусть для температуры Т «Хj, выбраны основной уровень Хj 0 =50° и интервал варьирования D Xj =20°, тогда кодированные значения будут равны соответственно для верхнего уровня  , для нижнего
, для нижнего  , для основного
, для основного  .
.
Кодированное значение фактора может быть вычислено для любого натурального его значения. Например, натуральному значению температуры Xj =100° соответствует кодированное значение 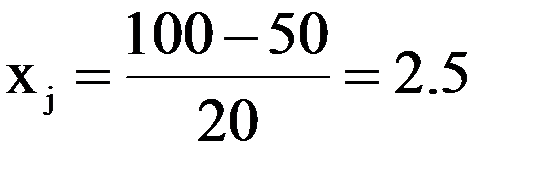 .
.
Выбор интервалов варьирования происходит часто в условиях противоречивых требований. Например, низкая точность фиксации уровня факторов требует увеличения интервалов варьирования.
С использованием кодированных значений –1, +1 могут быть построены матрицы планирования 2 k. С учетом концепции многофакторности варианты опытов эксперимента составляют полный набор комбинаций уровней факторов.
Строки в выделенных столбцах х1, х2, х3 матрицы планирования задают собственно план эксперимента, т. е. условия опытов, реализуемых при всех возможных комбинациях уровней факторов. В факторном пространстве эти строки задают координаты точек области экспериментирования.
Формальный прием построения плана эксперимента для варьируемых факторов заключается в следующем. Первая строка выбирается так, чтобы все изучаемые факторы находились на нижних уровнях, т. е. X 1 = – 1, X 2 = -1, X 3 = -1. Образование последующих строк плана эксперимента осуществляется так, чтобы при построчном переборе всех вариантов частота смены знака варьируемых факторов для каждого последующего фактора была вдвое меньше, чем предыдущего. Построенная по такому правилу матрица планирования для трех факторов показана в таблице 2. Геометрической интерпретацией ПФЭ 2 k является куб, координаты вершин которого задают условия опытов.
Обработка результатов эксперимента позволяет получить математическую модель изучаемого процесса (объекта) в виде уравнения регрессии, например для трехфакторного эксперимента:

Таблица 1.18
Матрица планирования эксперимента
| Номер опыта | Матрица планирования | Выход yi | |||||||
| x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2x3 | ||
| +1 +1 +1 +1 +1 +1 +1 +1 | -1 +1 -1 +1 -1 +1 -1 +1 | -1 -1 +1 +1 -1 -1 +1 +1 | -1 -1 -1 -1 +1 +1 +1 +1 | +1 -1 -1 +1 +1 -1 -1 +1 | +1 -1 +1 -1 -1 +1 -1 +1 | +1 +1 -1 -1 -1 -1 +1 +1 | -1 +1 +1 -1 +1 -1 -1 +1 | y1 y2 y3 y4 y5 y6 y7 y8 |
Коэффициенты уравнения регрессии показывают на влияние соответствующих факторов или их взаимодействий на выходной параметр (интенсивность изнашивания). Величина коэффициента характеризует значимость его в модели процесса, а знак указывает на результат изменения данного фактора.
Для удобства анализа полученной модели все незначимые факторы и их взаимодействия из модели удаляют, приравнивая коэффициенты при них нулю. После чего необходима обязательная проверка модели на адекватность.
В качестве примера реализации методики обработки результатов полнофакторного эксперимента предлагается протокол MathCad, в котором используются необходимые встроенные статистические функции, позволяющие существенно облегчить обработку данных.